
Question and Answers Forum
Question Number 90997 by jagoll last updated on 27/Apr/20

Commented by john santu last updated on 27/Apr/20
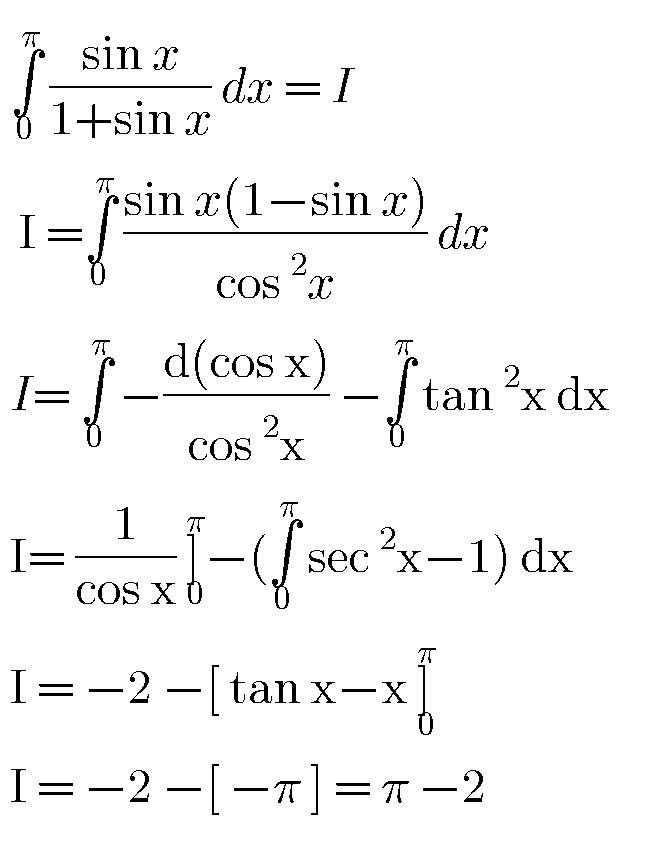
Commented by jagoll last updated on 27/Apr/20

Commented by mathmax by abdo last updated on 27/Apr/20
![I =∫_0 ^π ((sinx)/(1+sinx))dx ⇒ I =∫_0 ^π ((1+sinx−1)/(1+sinx))dx =π −∫_0 ^π (dx/(1+sinx)) we have ∫_0 ^π (dx/(1+sinx)) =_(tan((x/2))=t) ∫_0 ^∞ ((2dt)/((1+t^2 )(1+((2t)/(1+t^2 ))))) =∫_0 ^∞ ((2dt)/(1+t^2 +2t)) =∫_0 ^∞ ((2dt)/((t+1)^2 )) =−(2/(t+1))]_0 ^∞ =2 ⇒I =π−2](Q91050.png)
| ||
Question and Answers Forum | ||
Question Number 90997 by jagoll last updated on 27/Apr/20 | ||
 | ||
Commented by john santu last updated on 27/Apr/20 | ||
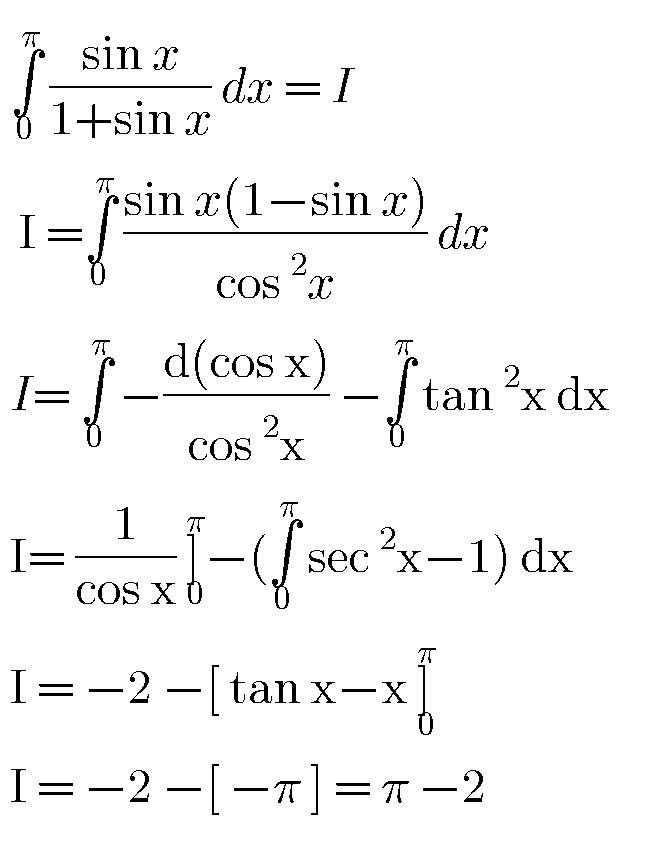 | ||
Commented by jagoll last updated on 27/Apr/20 | ||
 | ||
Commented by mathmax by abdo last updated on 27/Apr/20 | ||
![I =∫_0 ^π ((sinx)/(1+sinx))dx ⇒ I =∫_0 ^π ((1+sinx−1)/(1+sinx))dx =π −∫_0 ^π (dx/(1+sinx)) we have ∫_0 ^π (dx/(1+sinx)) =_(tan((x/2))=t) ∫_0 ^∞ ((2dt)/((1+t^2 )(1+((2t)/(1+t^2 ))))) =∫_0 ^∞ ((2dt)/(1+t^2 +2t)) =∫_0 ^∞ ((2dt)/((t+1)^2 )) =−(2/(t+1))]_0 ^∞ =2 ⇒I =π−2](Q91050.png) | ||