
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 91024 by john santu last updated on 27/Apr/20
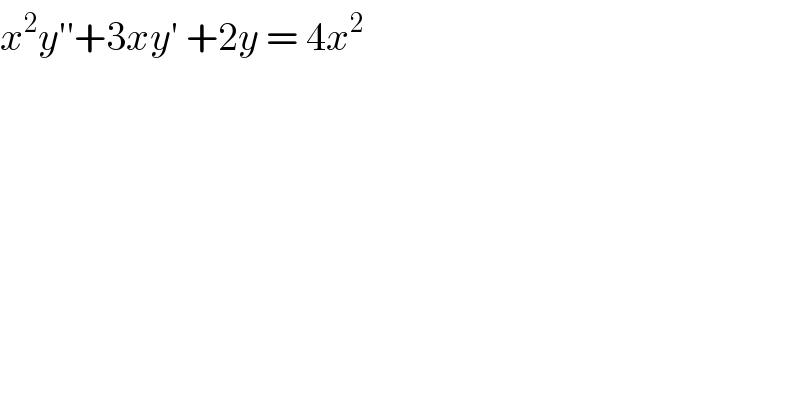
Commented by jagoll last updated on 27/Apr/20
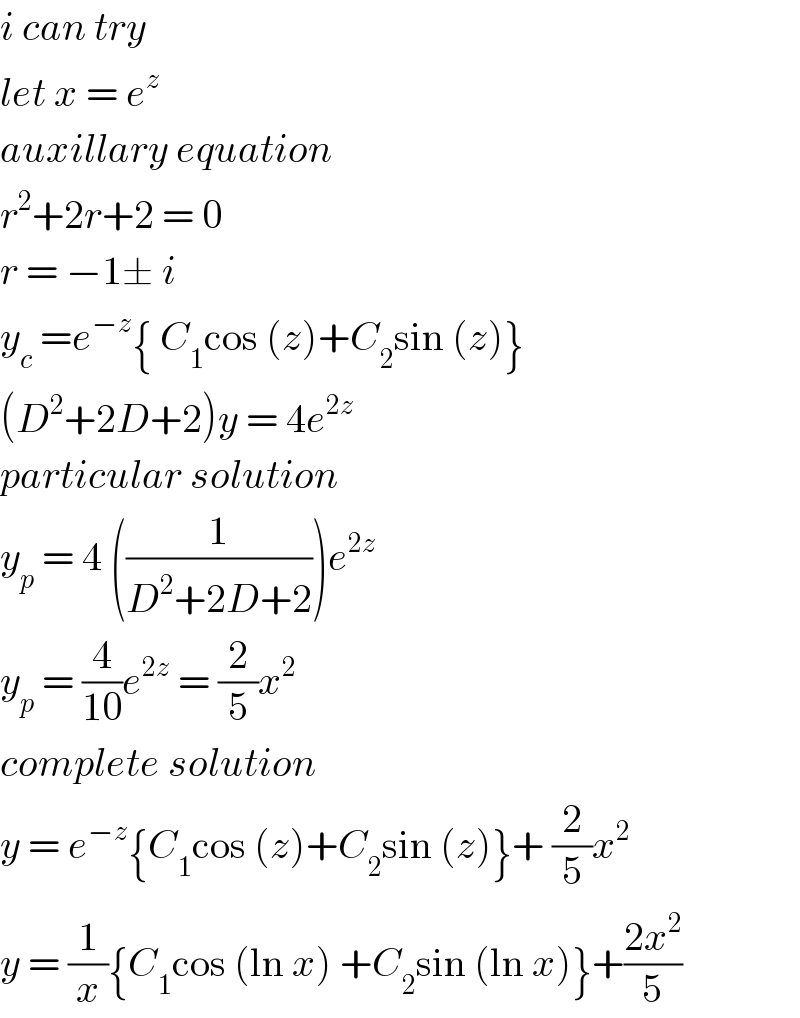
Commented by niroj last updated on 27/Apr/20
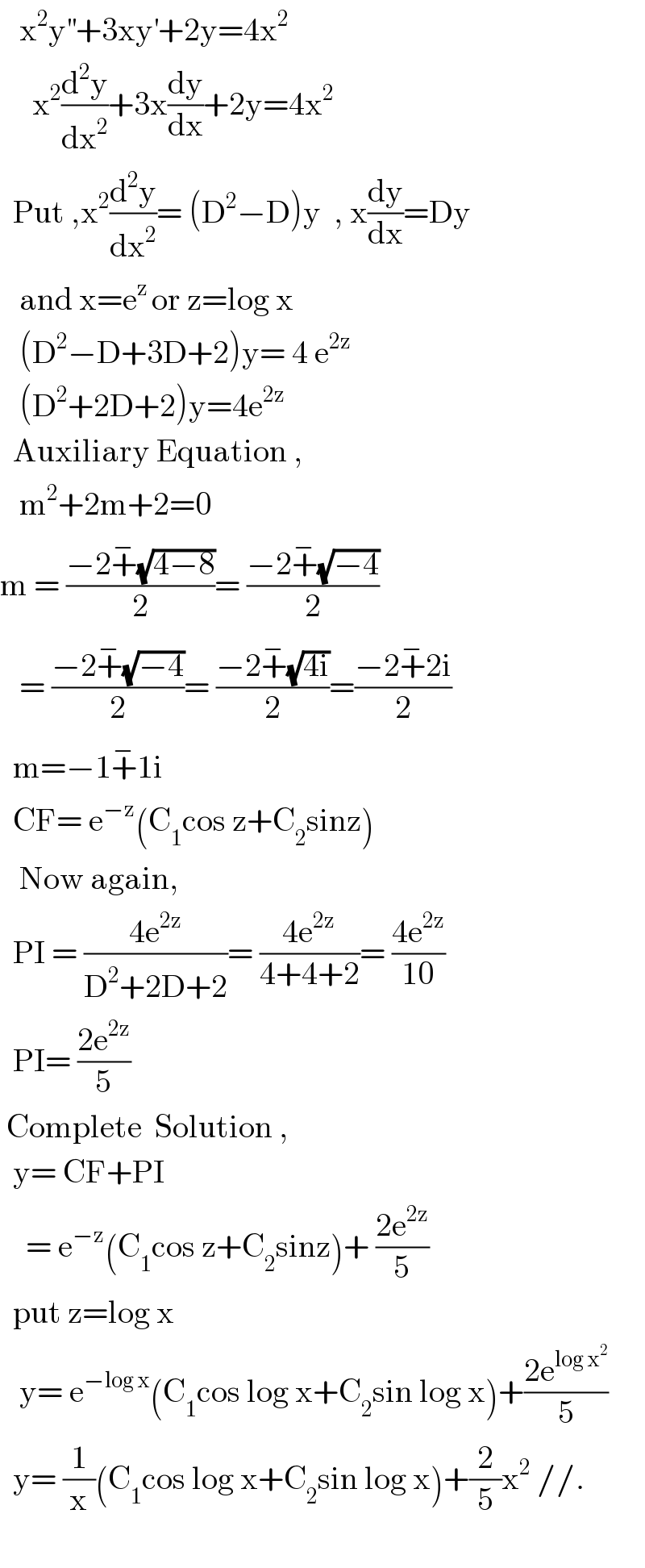
Commented by jagoll last updated on 27/Apr/20
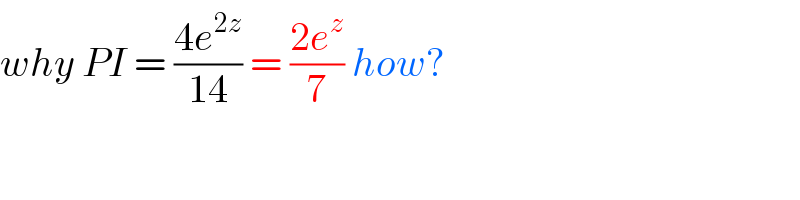
Commented by MWSuSon last updated on 27/Apr/20
Commented by niroj last updated on 27/Apr/20
Answered by MWSuSon last updated on 27/Apr/20
![let x=e^z x^2 y′′=D(D−1)y xy′=Dy D(D−1)y+3Dy+2y=4e^(2z) (D^2 +2D+2)y=4e^(2z) Auxillary eqution m^2 +2m+2=0 m=−1±i y_c =e^(−z) (C_1 cos (z)+C_2 sin (z)) y_p =4(1/(D^2 +2D+2))e^(2z) =4(1/(4+4+2))e^(2z) =((4e^(2z) )/(10)) =((2e^(2z) )/5) y=e^(−z) (C_1 cos (z)+C_2 sin (z))+(2/5)e^(2z) but z=log_e x y=(1/x)[C_1 cos (log_e x)+C_2 sin (log_e x)]+(2/5)x^2](Q91028.png)
