Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 9109 by tawakalitu last updated on 18/Nov/16

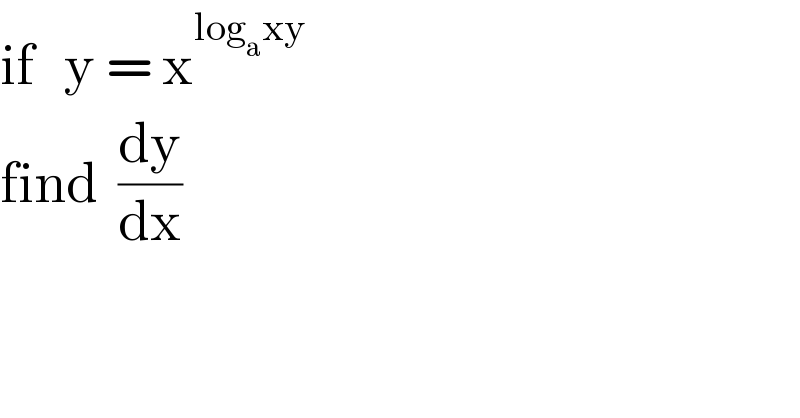
if y = x^(log_a xy) find (dy/dx)

$$\mathrm{if}\:\:\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{log}_{\mathrm{a}} \mathrm{xy}} \\ $$$$\mathrm{find}\:\:\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$

Answered by mrW last updated on 19/Nov/16

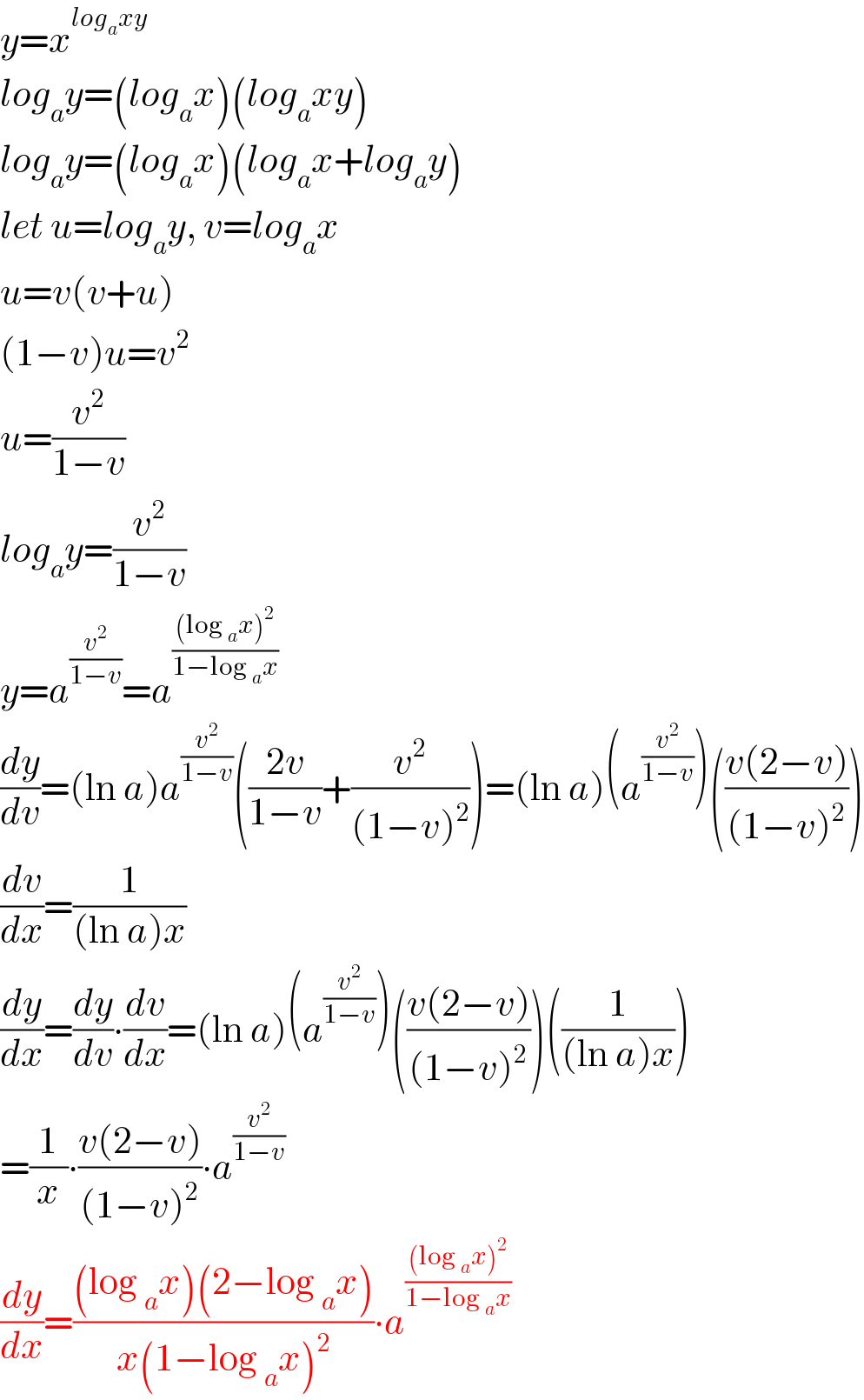
y=x^(log_a xy) log_a y=(log_a x)(log_a xy) log_a y=(log_a x)(log_a x+log_a y) let u=log_a y, v=log_a x u=v(v+u) (1−v)u=v^2 u=(v^2 /(1−v)) log_a y=(v^2 /(1−v)) y=a^(v^2 /(1−v)) =a^(((log _a x)^2 )/(1−log _a x)) (dy/dv)=(ln a)a^(v^2 /(1−v)) (((2v)/(1−v))+(v^2 /((1−v)^2 )))=(ln a)(a^(v^2 /(1−v)) )(((v(2−v))/((1−v)^2 ))) (dv/dx)=(1/((ln a)x)) (dy/dx)=(dy/dv)∙(dv/dx)=(ln a)(a^(v^2 /(1−v)) )(((v(2−v))/((1−v)^2 )))((1/((ln a)x))) =(1/x)∙((v(2−v))/((1−v)^2 ))∙a^(v^2 /(1−v)) (dy/dx)=(((log _a x)(2−log _a x))/(x(1−log _a x)^2 ))∙a^(((log _a x)^2 )/(1−log _a x))

$${y}={x}^{{log}_{{a}} {xy}} \\ $$$${log}_{{a}} {y}=\left({log}_{{a}} {x}\right)\left({log}_{{a}} {xy}\right) \\ $$$${log}_{{a}} {y}=\left({log}_{{a}} {x}\right)\left({log}_{{a}} {x}+{log}_{{a}} {y}\right) \\ $$$${let}\:{u}={log}_{{a}} {y},\:{v}={log}_{{a}} {x} \\ $$$${u}={v}\left({v}+{u}\right) \\ $$$$\left(\mathrm{1}−{v}\right){u}={v}^{\mathrm{2}} \\ $$$${u}=\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}} \\ $$$${log}_{{a}} {y}=\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}} \\ $$$${y}={a}^{\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}}} ={a}^{\frac{\left(\mathrm{log}\:_{{a}} {x}\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{log}\:_{{a}} {x}}} \\ $$$$\frac{{dy}}{{dv}}=\left(\mathrm{ln}\:{a}\right){a}^{\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}}} \left(\frac{\mathrm{2}{v}}{\mathrm{1}−{v}}+\frac{{v}^{\mathrm{2}} }{\left(\mathrm{1}−{v}\right)^{\mathrm{2}} }\right)=\left(\mathrm{ln}\:{a}\right)\left({a}^{\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}}} \right)\left(\frac{{v}\left(\mathrm{2}−{v}\right)}{\left(\mathrm{1}−{v}\right)^{\mathrm{2}} }\right) \\ $$$$\frac{{dv}}{{dx}}=\frac{\mathrm{1}}{\left(\mathrm{ln}\:{a}\right){x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dv}}\centerdot\frac{{dv}}{{dx}}=\left(\mathrm{ln}\:{a}\right)\left({a}^{\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}}} \right)\left(\frac{{v}\left(\mathrm{2}−{v}\right)}{\left(\mathrm{1}−{v}\right)^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\left(\mathrm{ln}\:{a}\right){x}}\right) \\ $$$$=\frac{\mathrm{1}}{{x}}\centerdot\frac{{v}\left(\mathrm{2}−{v}\right)}{\left(\mathrm{1}−{v}\right)^{\mathrm{2}} }\centerdot{a}^{\frac{{v}^{\mathrm{2}} }{\mathrm{1}−{v}}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\left(\mathrm{log}\:_{{a}} {x}\right)\left(\mathrm{2}−\mathrm{log}\:_{{a}} {x}\right)}{{x}\left(\mathrm{1}−\mathrm{log}\:_{{a}} {x}\right)^{\mathrm{2}} }\centerdot{a}^{\frac{\left(\mathrm{log}\:_{{a}} {x}\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{log}\:_{{a}} {x}}} \\ $$

Commented by tawakalitu last updated on 19/Nov/16

I really appreciate your effort sir. God bless you.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless} \\ $$$$\mathrm{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com