Question Number 91149 by Rio Michael last updated on 28/Apr/20
$$\mathrm{A}\:\mathrm{particle}\:\mathrm{starts}\:\mathrm{from}\:\mathrm{rest}\:\mathrm{and}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{on}\:\mathrm{a}\:\mathrm{smooth}\: \\ $$$$\mathrm{horizontal}\:\mathrm{surface}.\:\mathrm{Its}\:\mathrm{acceleration}\:\mathrm{at}\:\mathrm{time}\:{t}\:\mathrm{seconds}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:\mathrm{ms}^{−\mathrm{2}} \\ $$$$\mathrm{where}\:{k}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positve}\:\mathrm{constant}\:\mathrm{and}\:{v}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle}. \\ $$$$\mathrm{Given}\:\mathrm{that}\:{v}\:=\:\frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\:\mathrm{when}\:{t}\:=\:\mathrm{1}.\:\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{v}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{\mathrm{2}{t}} −\mathrm{1}\right) \\ $$
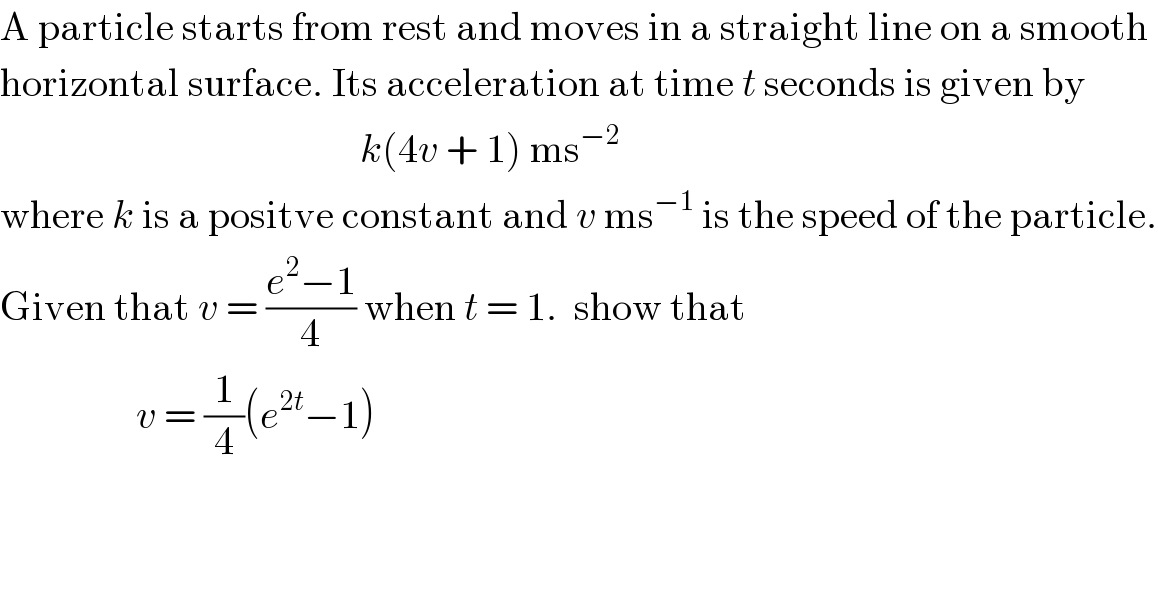
Commented by mr W last updated on 28/Apr/20
$${answer}\:{given}\:{is}\:{wrong} \\ $$
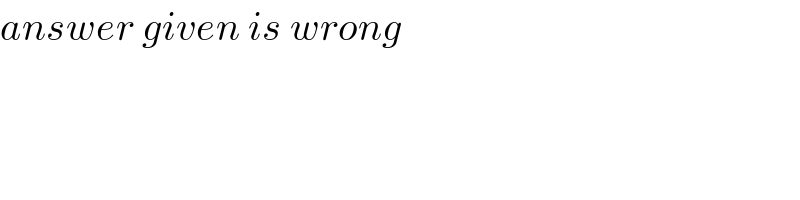
Answered by mr W last updated on 28/Apr/20
![a=(dv/dt)=k(4v+1) (dv/(4v+1))=kdt ∫(dv/(4v+1))=k∫dt (1/4)ln (4v+1)=kt+C (1/4)ln (4×((e^2 −1)/4)+1)=k+C (1/4)ln (e^2 )=k+C (1/4)[ln (4v+1)−ln (e^2 )]=k(t−1) (4v+1)e^(−2) =e^(4k(t−1)) ⇒v=(1/4)[e^(4k(t−1)+2) −1]](Q91152.png)
$${a}=\frac{{dv}}{{dt}}={k}\left(\mathrm{4}{v}+\mathrm{1}\right) \\ $$$$\frac{{dv}}{\mathrm{4}{v}+\mathrm{1}}={kdt} \\ $$$$\int\frac{{dv}}{\mathrm{4}{v}+\mathrm{1}}={k}\int{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{4}{v}+\mathrm{1}\right)={kt}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{4}×\frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}+\mathrm{1}\right)={k}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({e}^{\mathrm{2}} \right)={k}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\left(\mathrm{4}{v}+\mathrm{1}\right)−\mathrm{ln}\:\left({e}^{\mathrm{2}} \right)\right]={k}\left({t}−\mathrm{1}\right) \\ $$$$\left(\mathrm{4}{v}+\mathrm{1}\right){e}^{−\mathrm{2}} ={e}^{\mathrm{4}{k}\left({t}−\mathrm{1}\right)} \\ $$$$\Rightarrow{v}=\frac{\mathrm{1}}{\mathrm{4}}\left[{e}^{\mathrm{4}{k}\left({t}−\mathrm{1}\right)+\mathrm{2}} −\mathrm{1}\right] \\ $$
Commented by Rio Michael last updated on 28/Apr/20
![thank you sir,but i have some doubts, first sir: at t = 1, (1/4)ln(4v + 1) = kt + C is suppose to equal (1/4)ln(4v + 1) = k + C don′t understand why it equals C. also, (1/4)ln(e^2 ) = k + C ⇒ (1/4)ln(4v + 1) = k + C how′d you get (1/4)[ln(4v + 1)−ln(e^2 )] = kt???](Q91209.png)
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\mathrm{but}\:\mathrm{i}\:\mathrm{have}\:\mathrm{some}\:\mathrm{doubts}, \\ $$$$\mathrm{first}\:\mathrm{sir}:\:\mathrm{at}\:{t}\:=\:\mathrm{1},\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:=\:{kt}\:+\:{C}\:\mathrm{is}\:\mathrm{suppose}\:\mathrm{to}\:\mathrm{equal}\: \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:=\:{k}\:+\:{C}\:\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{why}\:\mathrm{it}\:\mathrm{equals}\:{C}. \\ $$$$\mathrm{also},\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left({e}^{\mathrm{2}} \right)\:=\:{k}\:+\:{C}\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:=\:{k}\:+\:{C} \\ $$$$\mathrm{how}'\mathrm{d}\:\mathrm{you}\:\mathrm{get}\:\:\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)−\mathrm{ln}\left({e}^{\mathrm{2}} \right)\right]\:=\:{kt}??? \\ $$$$ \\ $$
Commented by Rio Michael last updated on 28/Apr/20
![this is my approach sir,ofcourse from your method. at rest v= 0 a = k(4v + 1) ms^(−2) , k >0 a = (dv/dt) ⇒ (dv/dt) = k(4v+1) (dv/(4v+1)) = kdt ⇒ ∫(dv/(4v+1)) = k∫dt (1/4)ln (4v + 1) = kt + C at v = 0, t=0 ⇒ (1/4)ln(4(0) + 1) = C ⇒ C=0 now t = 1 ⇒ v = ((e^2 −1)/4) so (1/4)ln[4(((e^2 −1)/4))+1] = k ⇒k = 2 (1/4)ln(4v + 1) = 2k ⇒ v = (1/4)(e^(8t) −1)](Q91212.png)
$$\mathrm{this}\:\mathrm{is}\:\mathrm{my}\:\mathrm{approach}\:\mathrm{sir},\mathrm{ofcourse}\:\mathrm{from}\:\mathrm{your}\:\mathrm{method}. \\ $$$$\:\mathrm{at}\:\mathrm{rest}\:{v}=\:\mathrm{0}\: \\ $$$$\:{a}\:=\:{k}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:\mathrm{ms}^{−\mathrm{2}} \:,\:{k}\:>\mathrm{0} \\ $$$${a}\:=\:\frac{{dv}}{{dt}} \\ $$$$\Rightarrow\:\:\frac{{dv}}{{dt}}\:=\:{k}\left(\mathrm{4}{v}+\mathrm{1}\right) \\ $$$$\:\:\frac{{dv}}{\mathrm{4}{v}+\mathrm{1}}\:=\:{kdt}\:\Rightarrow\:\int\frac{{dv}}{\mathrm{4}{v}+\mathrm{1}}\:=\:{k}\int{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:=\:{kt}\:+\:{C} \\ $$$$\mathrm{at}\:{v}\:=\:\mathrm{0},\:{t}=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{4}\left(\mathrm{0}\right)\:+\:\mathrm{1}\right)\:=\:{C} \\ $$$$\Rightarrow\:{C}=\mathrm{0} \\ $$$$\mathrm{now}\:{t}\:=\:\mathrm{1}\:\Rightarrow\:{v}\:=\:\frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{so}\:\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left[\mathrm{4}\left(\frac{{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\right)+\mathrm{1}\right]\:=\:{k}\:\:\:\Rightarrow{k}\:=\:\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{4}{v}\:+\:\mathrm{1}\right)\:=\:\mathrm{2}{k}\:\Rightarrow\:{v}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{\mathrm{8}{t}} −\mathrm{1}\right) \\ $$