
Question and Answers Forum
Question Number 91185 by Tony Lin last updated on 28/Apr/20
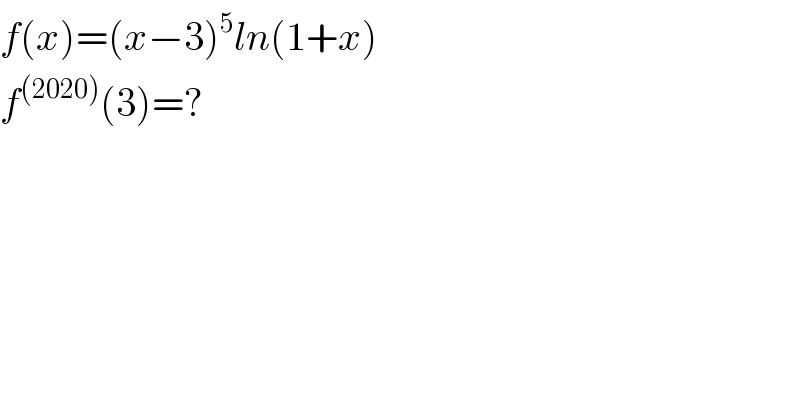
Commented by Tony Lin last updated on 28/Apr/20
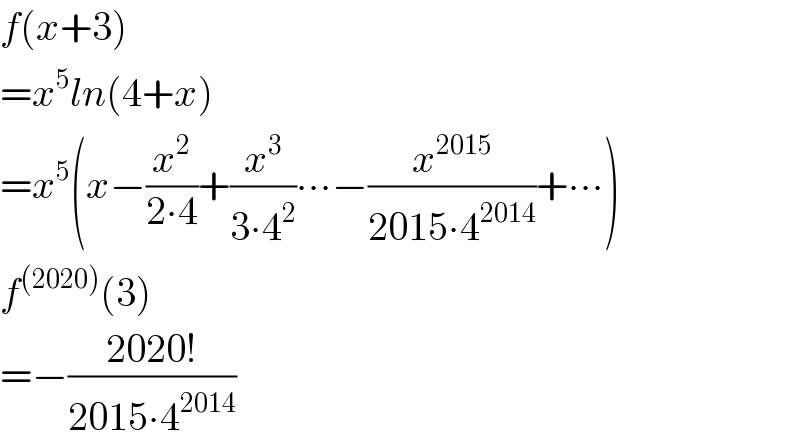
Commented by abdomathmax last updated on 28/Apr/20
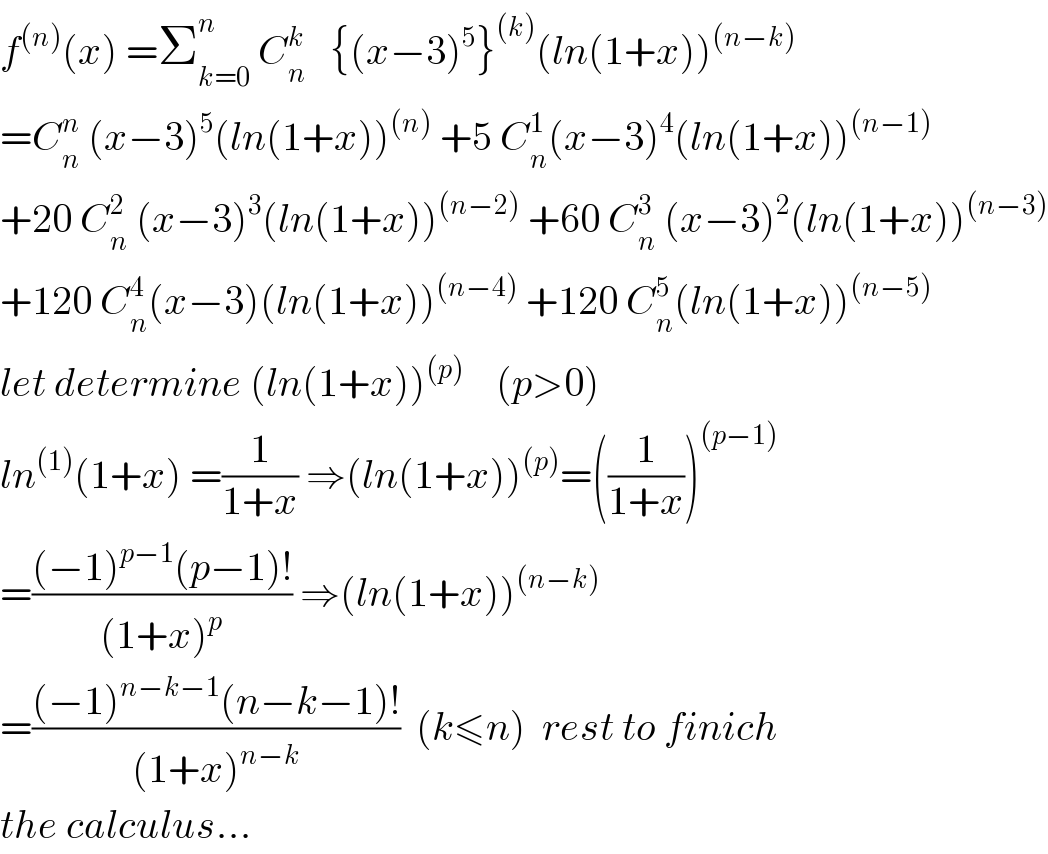
Answered by MWSuSon last updated on 28/Apr/20
![y=(x−3)^5 log_e (1+x) y_n =[(((−1)^(n−1) (n−1)!)/((1+x)^n ))(x−3)^5 +n(((−1)^(n−2) (n−2)!)/((1+x)^(n−1) ))5(x−3)^4 +((n(n−1))/2)(((−1)^(n−3) (n−3)!)/((1+x)^(n−2) ))20(x−3)^3 +((n(n−1)(n−2))/6)(((−1)^(n−4) (n−4)!)/((1+x)^(n−3) ))60(x−3)^2 +((n(n−1)(n−2)(n−3))/(24))(((−1)^(n−5) (n−5)!)/((x+1)^(n−4) ))120(x−3)+((n(n−1)(n−2)(n−3)(n−4))/(120))(((−1)^(n−6) (n−6)!)/((1+x)^(n−5) ))120] inserting 2020 where you see n and 3 where you see x you will have your answer. y_(2020) ∣_(x=3) =](Q91204.png)
| ||
Question and Answers Forum | ||
Question Number 91185 by Tony Lin last updated on 28/Apr/20 | ||
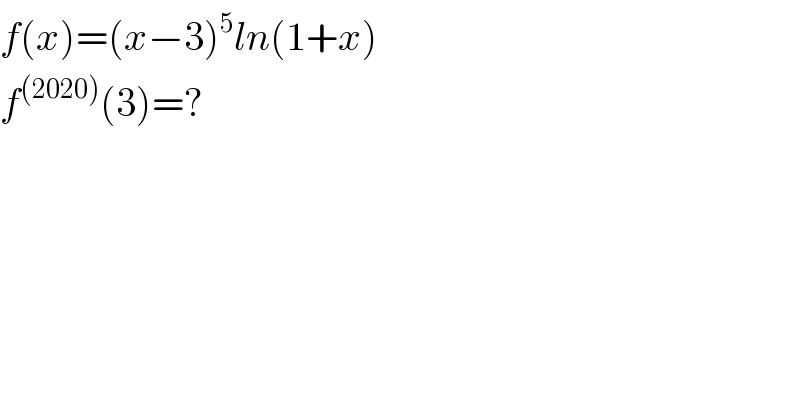 | ||
Commented by Tony Lin last updated on 28/Apr/20 | ||
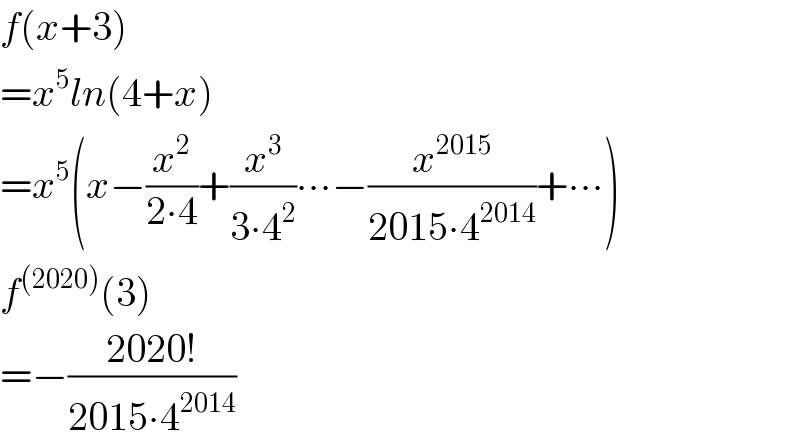 | ||
Commented by abdomathmax last updated on 28/Apr/20 | ||
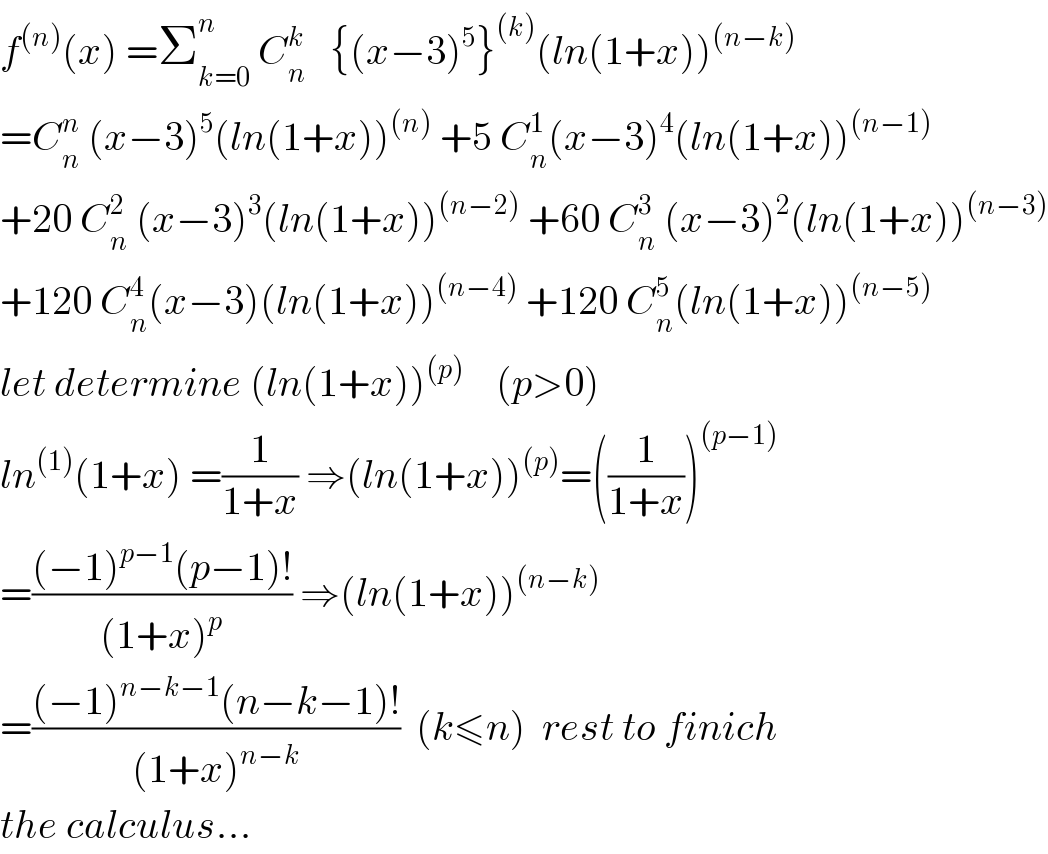 | ||
Answered by MWSuSon last updated on 28/Apr/20 | ||
![y=(x−3)^5 log_e (1+x) y_n =[(((−1)^(n−1) (n−1)!)/((1+x)^n ))(x−3)^5 +n(((−1)^(n−2) (n−2)!)/((1+x)^(n−1) ))5(x−3)^4 +((n(n−1))/2)(((−1)^(n−3) (n−3)!)/((1+x)^(n−2) ))20(x−3)^3 +((n(n−1)(n−2))/6)(((−1)^(n−4) (n−4)!)/((1+x)^(n−3) ))60(x−3)^2 +((n(n−1)(n−2)(n−3))/(24))(((−1)^(n−5) (n−5)!)/((x+1)^(n−4) ))120(x−3)+((n(n−1)(n−2)(n−3)(n−4))/(120))(((−1)^(n−6) (n−6)!)/((1+x)^(n−5) ))120] inserting 2020 where you see n and 3 where you see x you will have your answer. y_(2020) ∣_(x=3) =](Q91204.png) | ||
| ||