Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 91271 by mathmax by abdo last updated on 29/Apr/20

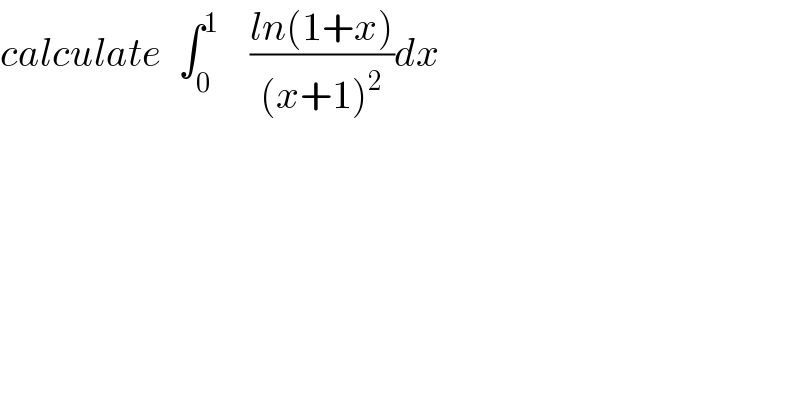
calculate ∫_0 ^1 ((ln(1+x))/((x+1)^2 ))dx

$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$

Commented by mathmax by abdo last updated on 29/Apr/20

I =∫_0 ^1 ((ln(1+x))/((x+1)^2 ))dx by psrts we get I =[−(1/(x+1))ln(x+1)]_0 ^1 +∫_0 ^1 ((ln(x+1))/(x+1))dx =−(1/2)ln(2) +∫_1 ^2 ((lnt)/t) dt (x+1=t) ∫_1 ^2 ((ln(t))/t) dt =_(lnt =u) ∫_0 ^(ln(2)) (u/e^u )e^u du =∫_0 ^(ln(2)) u du=[(u^2 /2)]_0 ^(ln(2)) =(1/2)ln^2 (2) ⇒ I =−(1/2)ln(2)+(1/2)ln^2 (2).

$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:{by}\:{psrts}\:{we}\:{get}\: \\ $$$${I}\:=\left[−\frac{\mathrm{1}}{{x}+\mathrm{1}}{ln}\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}+\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{lnt}}{{t}}\:{dt}\:\:\:\:\:\:\:\:\:\:\:\left({x}+\mathrm{1}={t}\right) \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{ln}\left({t}\right)}{{t}}\:{dt}\:=_{{lnt}\:={u}} \:\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \:\frac{{u}}{{e}^{{u}} }{e}^{{u}} \:{du}\:\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \:{u}\:{du}=\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\:\Rightarrow\:{I}\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right). \\ $$

Answered by  M±th+et+s last updated on 29/Apr/20

I=∫_0 ^1 ((ln(1+x))/(x^2 +1))dx put x=tan(u) dx=sec^2 (u) =∫_0 ^(π/4) ((ln(tan(u)+1))/(tan^2 u+1))sec^2 (u)du =∫_0 ^(π/4) ln(tan(u)+1)du =∫_0 ^(π/4) ln(((sinu+cosu)/(cosu)))du ∫_0 ^(π/4) ln(sinu+cosu)−ln(cosu) du ∫_0 ^(π/4) ln((√2)(cos((π/4)−u))−ln(cosu) du ∫_0 ^(π/4) ln((√2))+ln(cos((π/4)−u))−ln(cosu)du J=∫_0 ^(π/4) ln(cos((π/4)−u))du (π/4)−u=t du=−dt then J=∫_(π/4) ^0 −ln(cos(t))dt∫_0 ^(π/4) ln(cos(t))dt ∫_0 ^(π/4) ln(cos(t))dt=∫_0 ^(π/4) ln(cos(u))du then ∫_0 ^(π/4) ln((√2))+ln(cos(u))−ln(cos(u))du =∫_0 ^(π/4) ln((√2))du=ln(√2)(π/4)=(π/8)ln(2)

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${put}\:{x}={tan}\left({u}\right)\:\:\:\:{dx}={sec}^{\mathrm{2}} \left({u}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{ln}\left({tan}\left({u}\right)+\mathrm{1}\right)}{{tan}^{\mathrm{2}} {u}+\mathrm{1}}{sec}^{\mathrm{2}} \left({u}\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tan}\left({u}\right)+\mathrm{1}\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{sinu}+{cosu}}{{cosu}}\right){du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sinu}+{cosu}\right)−{ln}\left({cosu}\right)\:{du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)\right)−{ln}\left({cosu}\right)\:{du}\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}\right)+{ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)\right)−{ln}\left({cosu}\right){du} \\ $$$${J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)\right){du} \\ $$$$\frac{\pi}{\mathrm{4}}−{u}={t}\:\:\:\:{du}=−{dt} \\ $$$${then}\:{J}=\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} −{ln}\left({cos}\left({t}\right)\right){dt}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({u}\right)\right){du} \\ $$$$ \\ $$$${then}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}\right)+{ln}\left({cos}\left({u}\right)\right)−{ln}\left({cos}\left({u}\right)\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}\right){du}={ln}\sqrt{\mathrm{2}}\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 29/Apr/20

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented by  M±th+et+s last updated on 29/Apr/20

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Commented by mathmax by abdo last updated on 29/Apr/20

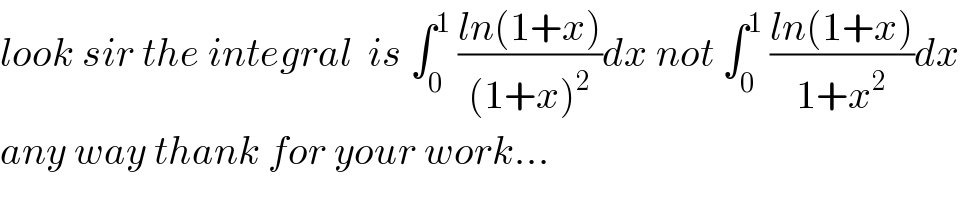
look sir the integral is ∫_0 ^1 ((ln(1+x))/((1+x)^2 ))dx not ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx any way thank for your work...

$${look}\:{sir}\:{the}\:{integral}\:\:{is}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}\:{not}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${any}\:{way}\:{thank}\:{for}\:{your}\:{work}... \\ $$

Commented by  M±th+et+s last updated on 29/Apr/20

sorry, i didn′t notice

$${sorry},\:{i}\:{didn}'{t}\:{notice} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com