
Question and Answers Forum
Question Number 91302 by 174 last updated on 29/Apr/20

Answered by MJS last updated on 29/Apr/20
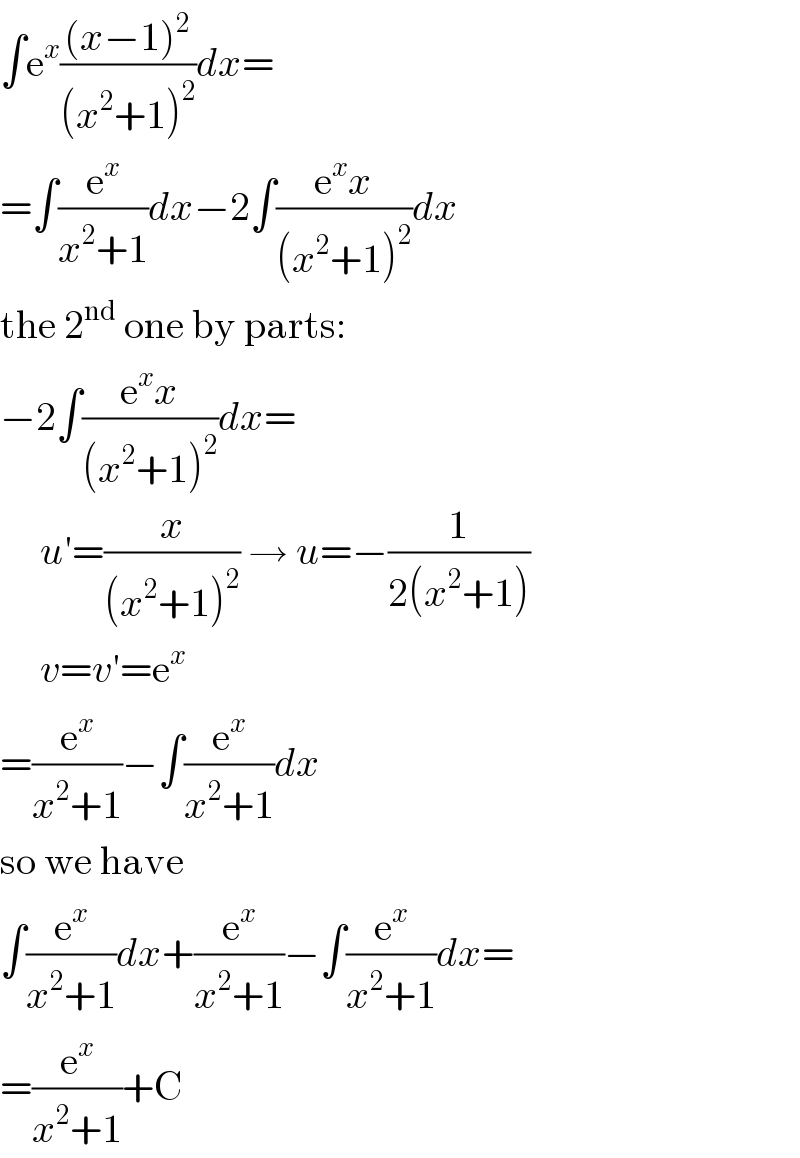
Answered by $@ty@m123 last updated on 29/Apr/20
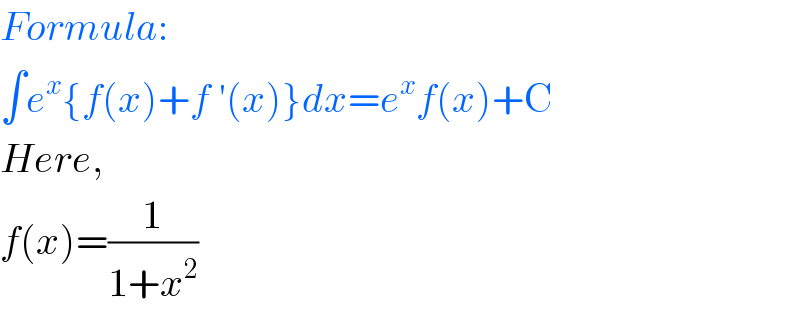
| ||
Question and Answers Forum | ||
Question Number 91302 by 174 last updated on 29/Apr/20 | ||
 | ||
Answered by MJS last updated on 29/Apr/20 | ||
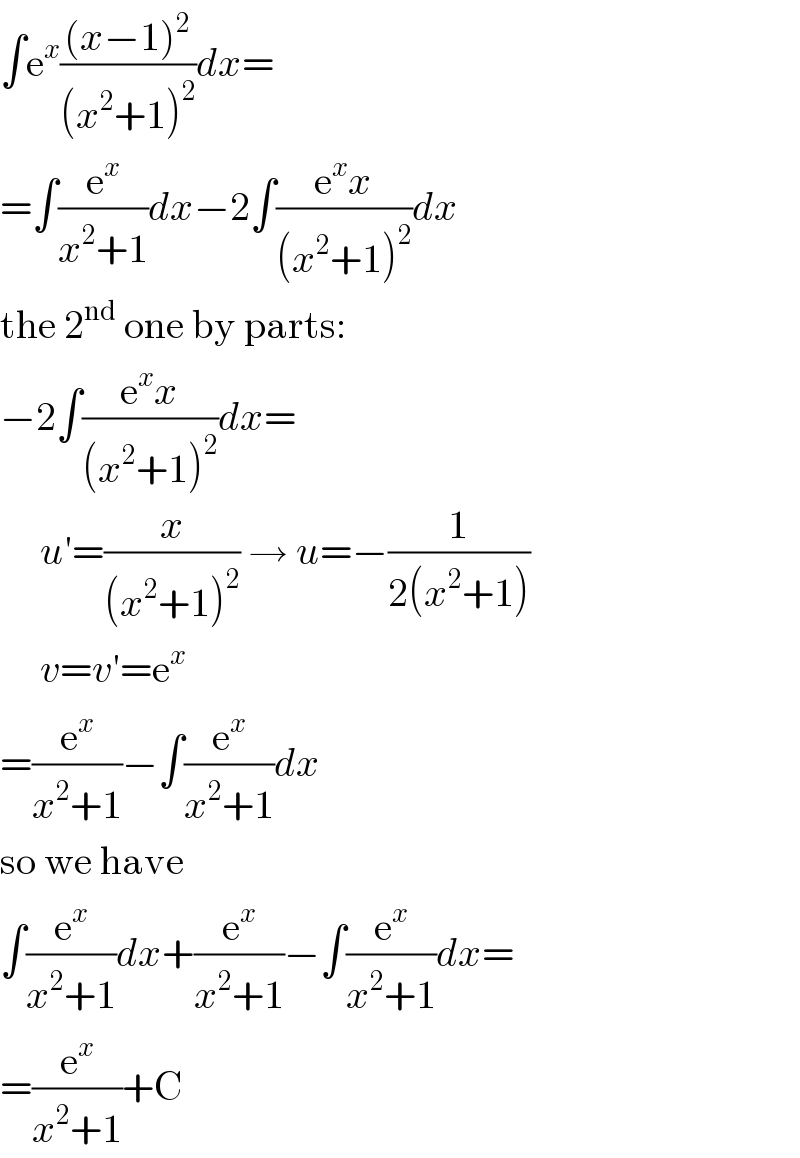 | ||
| ||
Answered by $@ty@m123 last updated on 29/Apr/20 | ||
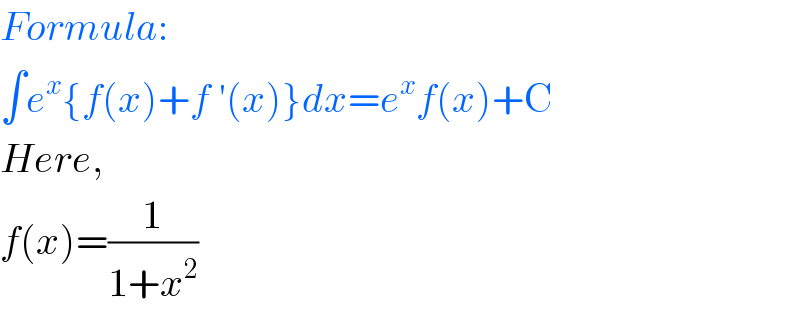 | ||
| ||