Question Number 91479 by Zainal Arifin last updated on 01/May/20
$$\:\underset{−\pi/\mathrm{2}\:} {\overset{\pi/\mathrm{2}} {\int}}\:\sqrt{\mathrm{cos}\:{x}−\mathrm{cos}^{\mathrm{3}} {x}}\:\mathrm{dx}=... \\ $$
Commented by jagoll last updated on 01/May/20
$$\sqrt{\mathrm{cos}\:{x}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)}\:=\:\sqrt{\mathrm{cos}\:{x}}\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\mathrm{0}} {\int}}\sqrt{\mathrm{cos}\:{x}}\:\left(−\mathrm{sin}\:{x}\right)\:{dx}\:+\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\sqrt{\mathrm{cos}\:{x}}\:\mathrm{sin}\:{x}\:{dx} \\ $$$${now}\:{easy}\:{to}\:{solve} \\ $$
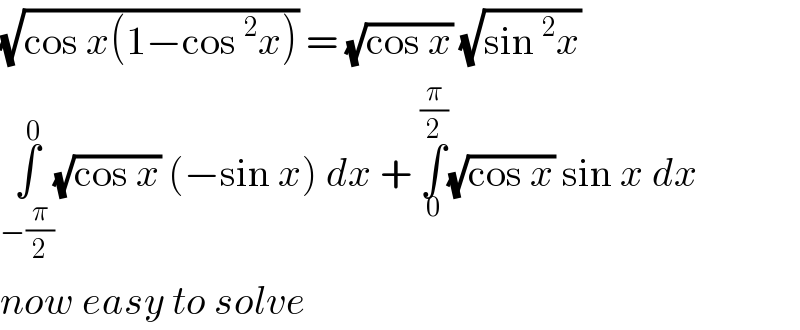
Commented by Zainal Arifin last updated on 01/May/20
$$\mathrm{Ok}.\:\mathrm{thanks} \\ $$
Commented by Prithwish Sen 1 last updated on 01/May/20
![∫(√(cosx)) sinx dx put cosx =t^2 ⇒−sinxdx=2tdt = −∫t.2t.dt = −(2/3).(cosx)^(3/2) ∫_(−(π/2)) ^(π/2) (√(cosx)).sinxdx = 2∫_0 ^(π/2) (√(cosx)).sinxdx=2[−(2/3)(cosx)^(2/3) ]_0 ^(π/2) =2.[−(0−(2/3))]=(4/3) please check.](Q91502.png)
$$\int\sqrt{\mathrm{cosx}}\:\mathrm{sinx}\:\mathrm{dx}\:\:\mathrm{put}\:\mathrm{cosx}\:=\mathrm{t}^{\mathrm{2}} \Rightarrow−\mathrm{sinxdx}=\mathrm{2tdt} \\ $$$$\:=\:−\int\mathrm{t}.\mathrm{2t}.\mathrm{dt}\:=\:−\frac{\mathrm{2}}{\mathrm{3}}.\left(\mathrm{cosx}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{cosx}}.\mathrm{sinxdx}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{cosx}}.\mathrm{sinxdx}=\mathrm{2}\left[−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{cosx}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{2}.\left[−\left(\mathrm{0}−\frac{\mathrm{2}}{\mathrm{3}}\right)\right]=\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by jagoll last updated on 01/May/20
$$\sqrt{\mathrm{sin}\:^{\mathrm{2}} {x}\:}\:\neq\:\mathrm{sin}\:{x} \\ $$$$\sqrt{\mathrm{sin}\:^{\mathrm{2}} {x}}\:=\:\mid\mathrm{sin}\:{x}\mid\: \\ $$
Answered by john santu last updated on 01/May/20
Commented by Prithwish Sen 1 last updated on 01/May/20
$$\mathrm{I}\:\mathrm{think}\:\:\mathrm{in}\:\:\mathrm{0}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}}\:\:\:\mathrm{sinx}\:\mathrm{and}\:\mathrm{cosx}\geqslant\:\mathrm{0} \\ $$$$\mathrm{sorry}\:\mathrm{fix}\:\mathrm{it}. \\ $$
Commented by jagoll last updated on 01/May/20
$$\mathrm{0}\leqslant{x}\geqslant\frac{\pi}{\mathrm{2}}\:=\:\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\:?\: \\ $$
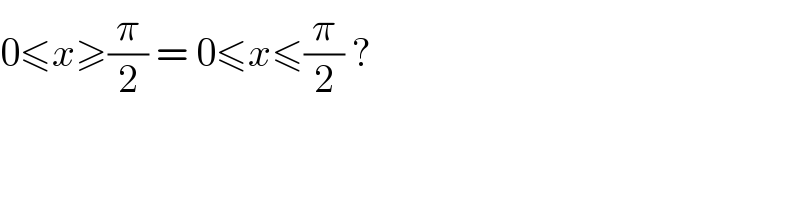
Commented by Prithwish Sen 1 last updated on 01/May/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$