
Question and Answers Forum
Question Number 91534 by M±th+et+s last updated on 01/May/20
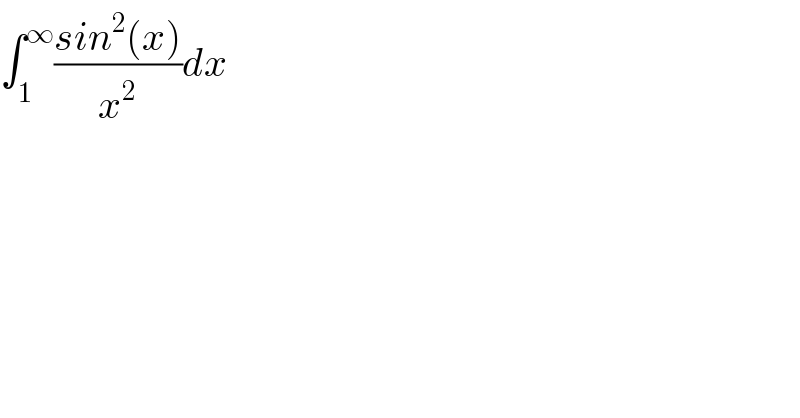
Commented by mathmax by abdo last updated on 01/May/20
![we have ∫_0 ^∞ ((sin^2 x)/x^2 )dx =∫_0 ^1 ((sin^2 x)/x^2 )dx +∫_1 ^∞ ((sin^2 x)/x^2 )dx ⇒ ∫_1 ^∞ ((sin^2 x)/x^2 )dx =∫_0 ^∞ ((sin^2 x)/x^2 )dx−∫_0 ^1 ((sin^2 x)/x^2 )dx we have by parts ∫_0 ^∞ ((sin^2 x)/x^2 )dx =[−(1/x)sin^2 x]_0 ^∞ +∫_0 ^∞ (1/x)(2sinx)cosx dx = ∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sint)/(t/2))×(dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) ∫_0 ^1 ((sin^2 x)/x^2 )dx =[−(1/x)sin^2 x]_0 ^1 +∫_0 ^1 (1/x)(2sinx)cosx dx =−sin^2 (1)+∫_0 ^1 ((sin(2x))/x)dx =−sin^2 (1)+ ∫_0 ^2 ((sint)/t)dt (t=2x) we have sint =t−(t^3 /6) +o(t^3 ) ⇒t−(t^3 /6)≤sint ≤t ⇒ 1−(t^2 /6)≤((sint)/t)≤1 ⇒ ∫_0 ^2 (1−(t^2 /6))dt≤∫_0 ^2 ((sint)/t)dt≤2 ⇒ [t−(t^3 /(18))]_0 ^2 ≤ ∫_0 ^2 ((sint)/t)dt ≤2 ⇒((14)/9) ≤ ∫_0 ^2 ((sint)/t) ≤2 ⇒ v_0 =(7/9) +1 =((16)/9) is approximate value for this integral ⇒ ∫_1 ^∞ ((sin^2 x)/x^2 )dx ∼ (π/2) +sin^2 (1)−((16)/9)](Q91589.png)
Commented by M±th+et+s last updated on 01/May/20
Commented by mathmax by abdo last updated on 01/May/20

| ||
Question and Answers Forum | ||
Question Number 91534 by M±th+et+s last updated on 01/May/20 | ||
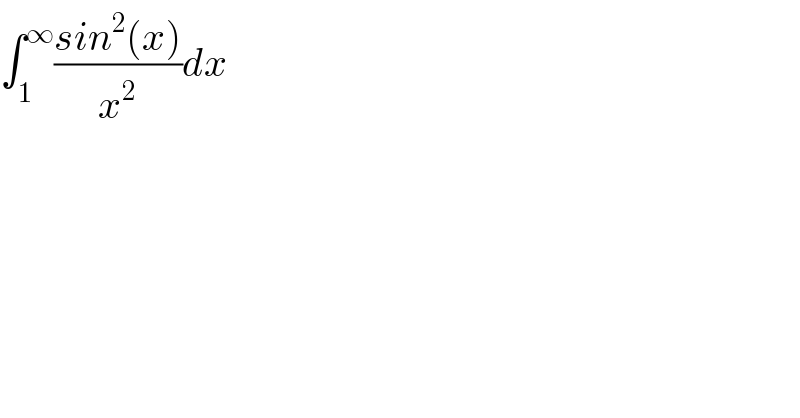 | ||
Commented by mathmax by abdo last updated on 01/May/20 | ||
![we have ∫_0 ^∞ ((sin^2 x)/x^2 )dx =∫_0 ^1 ((sin^2 x)/x^2 )dx +∫_1 ^∞ ((sin^2 x)/x^2 )dx ⇒ ∫_1 ^∞ ((sin^2 x)/x^2 )dx =∫_0 ^∞ ((sin^2 x)/x^2 )dx−∫_0 ^1 ((sin^2 x)/x^2 )dx we have by parts ∫_0 ^∞ ((sin^2 x)/x^2 )dx =[−(1/x)sin^2 x]_0 ^∞ +∫_0 ^∞ (1/x)(2sinx)cosx dx = ∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sint)/(t/2))×(dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) ∫_0 ^1 ((sin^2 x)/x^2 )dx =[−(1/x)sin^2 x]_0 ^1 +∫_0 ^1 (1/x)(2sinx)cosx dx =−sin^2 (1)+∫_0 ^1 ((sin(2x))/x)dx =−sin^2 (1)+ ∫_0 ^2 ((sint)/t)dt (t=2x) we have sint =t−(t^3 /6) +o(t^3 ) ⇒t−(t^3 /6)≤sint ≤t ⇒ 1−(t^2 /6)≤((sint)/t)≤1 ⇒ ∫_0 ^2 (1−(t^2 /6))dt≤∫_0 ^2 ((sint)/t)dt≤2 ⇒ [t−(t^3 /(18))]_0 ^2 ≤ ∫_0 ^2 ((sint)/t)dt ≤2 ⇒((14)/9) ≤ ∫_0 ^2 ((sint)/t) ≤2 ⇒ v_0 =(7/9) +1 =((16)/9) is approximate value for this integral ⇒ ∫_1 ^∞ ((sin^2 x)/x^2 )dx ∼ (π/2) +sin^2 (1)−((16)/9)](Q91589.png) | ||
Commented by M±th+et+s last updated on 01/May/20 | ||
 | ||
Commented by mathmax by abdo last updated on 01/May/20 | ||
 | ||