Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 91613 by  M±th+et+s last updated on 01/May/20

$$solvewithoutusing{l}^{\prime }hopital$$$$\underset{x\to e}{lim}\frac{ln\left(x\right)-1}{\frac{e}{x}-1}$$

Commented by abdomathmax last updated on 01/May/20

$$changement\frac{e}{x}=tgive\frac{x}{e}=\frac{1}{t}\Rightarrow x=\frac{e}{t}$$$${lim}_{x\to e}\frac{ln\left(x\right)-1}{\frac{e}{x}-1}={lim}_{t\to 1}\frac{ln\left(\frac{e}{t}\right)-1}{t-1}$$$$={lim}_{t\to 1}\frac{-lnt}{t-1}=-{lim}_{t\to 1}\frac{ln\left(t\right)}{t-1}=-1$$

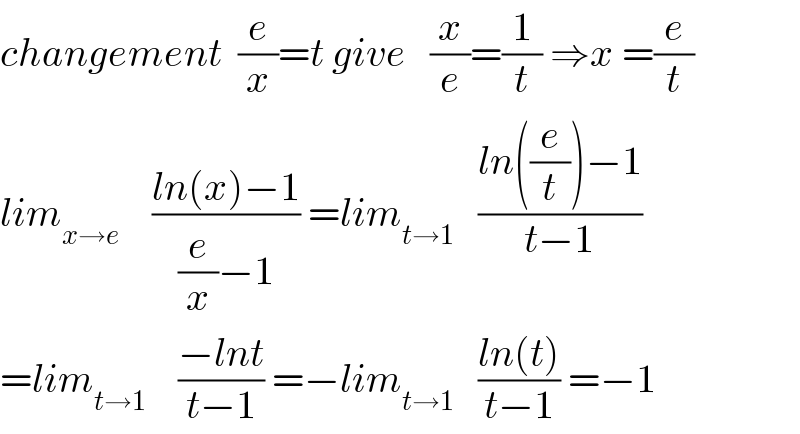
Commented by  M±th+et+s last updated on 01/May/20

$$thankyousir$$

Commented by arcana last updated on 02/May/20

$$\mathrm{why}\underset{t\to 1}{\lim }\frac{\ln \left(t\right)}{t-1}=1\mathrm{without}{\mathrm{L}}^{\prime }\mathrm{Hopital}?$$

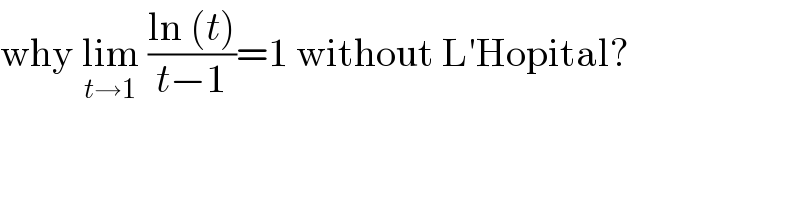
Commented by mathmax by abdo last updated on 02/May/20

$${lim}_{t\to t_0}\frac{f\left(t\right)-f\left(t_0\right)}{t-t_0}=f^{{}^{\prime }}\left(t_0\right)so$$$${lim}_{t\to 1}\frac{ln\left(t\right)}{t-1}={lim}_{t\to 1}\frac{ln\left(t\right)-ln\left(1\right)}{t-1}={ln}^{{}^{\prime }}\left(1\right)=1$$$$({ln}^{{}^{\prime }}\left(t\right)=\frac{1}{t})$$

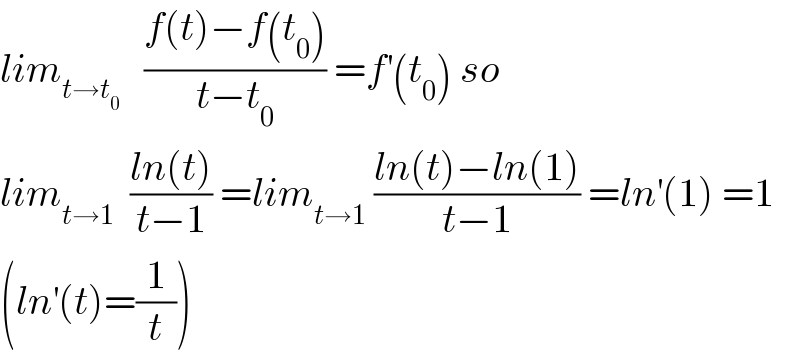
Answered by mr W last updated on 02/May/20

$$lett=\frac{e}{x}-1$$$$x\to e\Rightarrow t\to 0$$$$\Rightarrow x=\frac{e}{1+t}$$$$\underset{x\to e}{lim}\frac{ln\left(x\right)-1}{\frac{e}{x}-1}$$$$=\underset{t\to 0}{\lim }\frac{\ln \frac{e}{1+t}-1}{t}$$$$=-\underset{t\to 0}{\lim }\frac{\ln (1+t)}{t}$$$$=-\underset{t\to 0}{\lim }\left\{\ln {(1+t)}^{\frac{1}{t}}\right\}$$$$=-\underset{n\to \mathrm{\infty }}{\lim }\left\{\ln {(1+\frac{1}{n})}^n\right\}\leftarrow definitionofe$$$$=-\ln e$$$$=-1$$

Commented by  M±th+et+s last updated on 02/May/20

$$godblessyousir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com