Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 91655 by Rio Michael last updated on 02/May/20

A particle is projected with an intial velocity of u ms^(−1) at an angle α to the ground from a point O on the ground. Given that it clears two walls of hieght h and distances 2h and 4h respectively from O. (a) find the tangent of α (b) the maximum hieght (c) the range and period of the particle (d) show that u^2 = (4/(26)) gh please sir can you help me using the actual equations of projectile motion?

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{with}\:\mathrm{an}\:\mathrm{intial}\:\mathrm{velocity}\:\mathrm{of}\:{u}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\alpha\:\mathrm{to}\: \\ $$$$\mathrm{the}\:\mathrm{ground}\:\mathrm{from}\:\mathrm{a}\:\mathrm{point}\:\mathrm{O}\:\mathrm{on}\:\mathrm{the}\:\mathrm{ground}.\:\mathrm{Given}\:\mathrm{that}\:\mathrm{it}\:\mathrm{clears} \\ $$$$\mathrm{two}\:\mathrm{walls}\:\mathrm{of}\:\mathrm{hieght}\:{h}\:\mathrm{and}\:\mathrm{distances}\:\mathrm{2h}\:\mathrm{and}\:\mathrm{4h}\:\mathrm{respectively}\:\mathrm{from}\:\mathrm{O}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{of}\:\alpha \\ $$$$\left(\mathrm{b}\right)\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{hieght} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{the}\:\mathrm{range}\:\mathrm{and}\:\mathrm{period}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\left(\mathrm{d}\right)\:\mathrm{show}\:\mathrm{that}\:{u}^{\mathrm{2}} \:=\:\frac{\mathrm{4}}{\mathrm{26}}\:\mathrm{g}{h}\: \\ $$$$\mathrm{please}\:\mathrm{sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}\:\mathrm{using}\:\mathrm{the}\:\mathrm{actual}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{projectile}\:\mathrm{motion}? \\ $$$$ \\ $$

Commented by Rio Michael last updated on 02/May/20

no sir, not clear, i still have difficulties solving the problem using your method.

$$\mathrm{no}\:\mathrm{sir},\:\mathrm{not}\:\mathrm{clear},\:\mathrm{i}\:\mathrm{still}\:\mathrm{have}\:\mathrm{difficulties}\:\mathrm{solving} \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{using}\:\mathrm{your}\:\mathrm{method}. \\ $$

Commented by mr W last updated on 02/May/20

i thought all is clear in Q89319.

$${i}\:{thought}\:{all}\:{is}\:{clear}\:{in}\:{Q}\mathrm{89319}. \\ $$

Commented by mr W last updated on 03/May/20

actually there are only three things one has to know: 1. the track of the ball is a parabola. 2. a parabola is a symmetric curve. 3. with respect to the vertex of a parabola the y−coordinate of a point is proportional to the square of its x−coordinate, see diagram, i.e. (y_2 /y_1 )=((x_2 /x_1 ))^2 i think you know all these already. so what you should do is to apply these.

$${actually}\:{there}\:{are}\:{only}\:{three}\:{things} \\ $$$${one}\:{has}\:{to}\:{know}: \\ $$$$\mathrm{1}.\:{the}\:{track}\:{of}\:{the}\:{ball}\:{is}\:{a}\:{parabola}. \\ $$$$\mathrm{2}.\:{a}\:{parabola}\:{is}\:{a}\:{symmetric}\:{curve}. \\ $$$$\mathrm{3}.\:{with}\:{respect}\:{to}\:{the}\:{vertex}\:{of}\:{a} \\ $$$${parabola}\:{the}\:{y}−{coordinate}\:{of}\:{a}\:{point}\:{is}\: \\ $$$${proportional}\:{to}\:{the}\:{square}\:{of}\:{its} \\ $$$${x}−{coordinate},\:{see}\:{diagram},\:{i}.{e}. \\ $$$$\frac{{y}_{\mathrm{2}} }{{y}_{\mathrm{1}} }=\left(\frac{{x}_{\mathrm{2}} }{{x}_{\mathrm{1}} }\right)^{\mathrm{2}} \\ $$$${i}\:{think}\:{you}\:{know}\:{all}\:{these}\:{already}.\:{so} \\ $$$${what}\:{you}\:{should}\:{do}\:{is}\:{to}\:{apply}\:{these}. \\ $$

Commented by mr W last updated on 02/May/20

Commented by Rio Michael last updated on 02/May/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Rio Michael last updated on 02/May/20

okay sir mr W i really have problems with this particular projectile problem, but sir please check this out. range = 2h + 2h + 2h = 6h for maximum height using : (y_1 /y_2 ) = ((x_1 /x_2 ))^2 ⇒ (h_(max) /h) = (((3h)^2 )/h^2 ) ⇒ h_(max) = 9h sir why doesn′t this match your previous answer.

$$\mathrm{okay}\:\mathrm{sir}\:\mathrm{mr}\:\mathrm{W}\:\mathrm{i}\:\mathrm{really}\:\mathrm{have}\:\mathrm{problems}\:\mathrm{with}\:\mathrm{this}\:\mathrm{particular}\:\mathrm{projectile} \\ $$$$\mathrm{problem},\:\mathrm{but}\:\mathrm{sir}\:\mathrm{please}\:\mathrm{check}\:\mathrm{this}\:\mathrm{out}. \\ $$$$\:\mathrm{range}\:=\:\mathrm{2}{h}\:+\:\mathrm{2}{h}\:+\:\mathrm{2}{h}\:=\:\mathrm{6}{h} \\ $$$$\mathrm{for}\:\mathrm{maximum}\:\mathrm{height}\:\mathrm{using}\::\:\frac{{y}_{\mathrm{1}} }{{y}_{\mathrm{2}} }\:=\:\left(\frac{{x}_{\mathrm{1}} }{{x}_{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{h}_{\mathrm{max}} }{{h}}\:=\:\frac{\left(\mathrm{3}{h}\right)^{\mathrm{2}} }{{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{h}_{\mathrm{max}} \:=\:\mathrm{9}{h}\:\mathrm{sir}\:\mathrm{why}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{this}\:\mathrm{match}\:\mathrm{your}\:\mathrm{previous}\:\mathrm{answer}. \\ $$

Commented by mr W last updated on 02/May/20

you should apply the formula in the way as the parabola in the diagram! i have said: to apply the formula the y−coordinate and x−coordinate must be with respect to the vertex, that should be clear! in your case it is: (h_(max) /(h_(max) −h))=(((3h)/h))^2

$${you}\:{should}\:{apply}\:{the}\:{formula}\:{in}\:{the} \\ $$$${way}\:{as}\:{the}\:{parabola}\:{in}\:{the}\:{diagram}! \\ $$$${i}\:{have}\:{said}:\:{to}\:{apply}\:{the}\:{formula}\:{the} \\ $$$${y}−{coordinate}\:{and}\:{x}−{coordinate}\:{must} \\ $$$${be}\:{with}\:{respect}\:{to}\:{the}\:{vertex},\:{that} \\ $$$${should}\:{be}\:{clear}! \\ $$$${in}\:{your}\:{case}\:{it}\:{is}: \\ $$$$\frac{{h}_{{max}} }{{h}_{{max}} −{h}}=\left(\frac{\mathrm{3}{h}}{{h}}\right)^{\mathrm{2}} \\ $$

Commented by mr W last updated on 02/May/20

Commented by mr W last updated on 02/May/20

Commented by Rio Michael last updated on 02/May/20

oh thank God sir i finally got it thanks

$$\mathrm{oh}\:\mathrm{thank}\:\mathrm{God}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{finally}\:\mathrm{got}\:\mathrm{it}\:\mathrm{thanks} \\ $$

Commented by mr W last updated on 02/May/20

never just apply a formula before one has understood it!

$${never}\:{just}\:{apply}\:{a}\:{formula}\:{before} \\ $$$${one}\:{has}\:{understood}\:{it}! \\ $$

Commented by Rio Michael last updated on 02/May/20

okay sir thanks

$$\mathrm{okay}\:\mathrm{sir}\:\mathrm{thanks} \\ $$

Answered by mr W last updated on 03/May/20

Method I (quick and safe, but one should have deep understanding about projectile motion and the features of parabola)

$$\boldsymbol{{Method}}\:\boldsymbol{{I}}\:\left({quick}\:{and}\:{safe},\:{but}\:{one}\right. \\ $$$${should}\:{have}\:{deep}\:{understanding}\:{about} \\ $$$${projectile}\:{motion}\:{and}\:{the}\:{features} \\ $$$$\left.{of}\:{parabola}\right) \\ $$

Commented by mr W last updated on 03/May/20

Commented by mr W last updated on 03/May/20

the track of the ball is a parabola which is symmetric about the position where it reaches the highest point. since the ball reaches two walls with the same hight h, the highest point (symmetry point) must be exactly in the middle of these two walls, see diagram. the track section DBC is the mirror image of OAD about point D. range R=OC=2h+2h+2h=6h (h_(max) /(h_(max) −h))=(((3h)/h))^2 =9 ⇒h_(max) =(9/8)h tan θ=((2h_(max) )/(3h))=((2×9h)/(8×3h))=(3/4) (θ=α in qn.) time from O to D is the same as time from D to C=(T/2)=time which a ball needs for a free fall from hight h_(max) to the ground. (T/2)=(√((2h_(max) )/g)) ⇒period T=2(√((2×9h)/(8g)))=3(√(h/g)) in time T the ball moves a horizontal distance R=6h, u cos θ T=R ⇒u=((6h)/(cos θ T))=((6h)/T)×(√(tan^2 θ+1)) ⇒u=((6h)/(3(√(h/g))))×(√(((3/4))^2 +1))=((5(√(gh)))/2) (u^2 =(4/(26))gh given in question is wrong!)

$${the}\:{track}\:{of}\:{the}\:{ball}\:{is}\:{a}\:{parabola}\:{which} \\ $$$${is}\:{symmetric}\:{about}\:{the}\:{position}\:{where} \\ $$$${it}\:{reaches}\:{the}\:{highest}\:{point}. \\ $$$${since}\:{the}\:{ball}\:{reaches}\:{two}\:{walls}\:{with} \\ $$$${the}\:{same}\:{hight}\:{h},\:{the}\:{highest}\:{point} \\ $$$$\left({symmetry}\:{point}\right)\:{must}\:{be}\:{exactly}\:{in}\:{the} \\ $$$${middle}\:{of}\:{these}\:{two}\:{walls},\:{see}\:{diagram}. \\ $$$${the}\:{track}\:{section}\:{DBC}\:{is}\:{the}\:{mirror} \\ $$$${image}\:{of}\:{OAD}\:{about}\:{point}\:{D}. \\ $$$$ \\ $$$${range}\:{R}={OC}=\mathrm{2}{h}+\mathrm{2}{h}+\mathrm{2}{h}=\mathrm{6}{h} \\ $$$$ \\ $$$$\frac{{h}_{{max}} }{{h}_{{max}} −{h}}=\left(\frac{\mathrm{3}{h}}{{h}}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{h}_{{max}} =\frac{\mathrm{9}}{\mathrm{8}}{h} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}{h}_{{max}} }{\mathrm{3}{h}}=\frac{\mathrm{2}×\mathrm{9}{h}}{\mathrm{8}×\mathrm{3}{h}}=\frac{\mathrm{3}}{\mathrm{4}}\:\left(\theta=\alpha\:{in}\:{qn}.\right) \\ $$$$ \\ $$$${time}\:{from}\:{O}\:{to}\:{D}\:{is}\:{the}\:{same}\:{as}\:{time} \\ $$$${from}\:{D}\:{to}\:{C}=\frac{{T}}{\mathrm{2}}={time}\:{which}\:{a}\:{ball} \\ $$$${needs}\:{for}\:{a}\:{free}\:{fall}\:{from}\:{hight}\:{h}_{{max}} \\ $$$${to}\:{the}\:{ground}. \\ $$$$\frac{{T}}{\mathrm{2}}=\sqrt{\frac{\mathrm{2}{h}_{{max}} }{{g}}} \\ $$$$\Rightarrow{period}\:{T}=\mathrm{2}\sqrt{\frac{\mathrm{2}×\mathrm{9}{h}}{\mathrm{8}{g}}}=\mathrm{3}\sqrt{\frac{{h}}{{g}}} \\ $$$$ \\ $$$${in}\:{time}\:{T}\:{the}\:{ball}\:{moves}\:{a}\:{horizontal} \\ $$$${distance}\:{R}=\mathrm{6}{h}, \\ $$$${u}\:\mathrm{cos}\:\theta\:{T}={R} \\ $$$$\Rightarrow{u}=\frac{\mathrm{6}{h}}{\mathrm{cos}\:\theta\:{T}}=\frac{\mathrm{6}{h}}{{T}}×\sqrt{\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{1}} \\ $$$$\Rightarrow{u}=\frac{\mathrm{6}{h}}{\mathrm{3}\sqrt{\frac{{h}}{{g}}}}×\sqrt{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{5}\sqrt{{gh}}}{\mathrm{2}} \\ $$$$ \\ $$$$\left({u}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{26}}{gh}\:{given}\:{in}\:{question}\:{is}\:{wrong}!\right) \\ $$

Commented by Rio Michael last updated on 03/May/20

wow sir thanks so much again. I don′t know why this particular projectile motion problem dealt with my understanding. Guess i have to take a whole course on this again ,including parabolic paths.

$$\mathrm{wow}\:\mathrm{sir}\:\mathrm{thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{again}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{why} \\ $$$$\mathrm{this}\:\mathrm{particular}\:\mathrm{projectile}\:\mathrm{motion}\:\mathrm{problem}\:\mathrm{dealt}\:\mathrm{with}\: \\ $$$$\mathrm{my}\:\mathrm{understanding}.\:\mathrm{Guess}\:\mathrm{i}\:\mathrm{have}\:\mathrm{to}\:\mathrm{take}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{course} \\ $$$$\mathrm{on}\:\mathrm{this}\:\mathrm{again}\:,\mathrm{including}\:\mathrm{parabolic}\:\mathrm{paths}. \\ $$

Answered by mr W last updated on 03/May/20

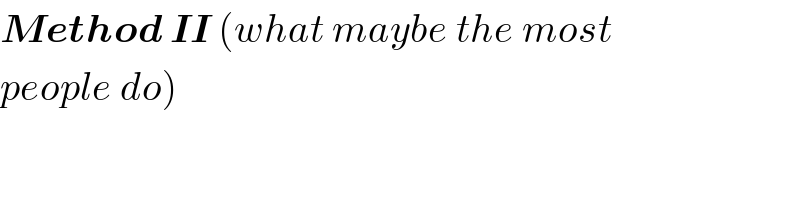
Method II (what maybe the most people do)

$$\boldsymbol{{Method}}\:\boldsymbol{{II}}\:\left({what}\:{maybe}\:{the}\:{most}\right. \\ $$$$\left.{people}\:{do}\right) \\ $$

Commented by mr W last updated on 03/May/20

Commented by mr W last updated on 03/May/20

x=u cos θ t y=u sin θ t−(1/2)gt^2 x_A =u cos θ t_A =2h y_A =u sin θ t_A −(1/2)gt_A ^2 =h x_B =u cos θ t_B =4h y_B =u sin θ t_B −(1/2)gt_B ^2 =h x_B −x_A =u cos θ (t_B −t_A )=4h−2h=2h ⇒t_B −t_A =((2h)/(u cos θ)) y_B −y_B =u sin θ (t_B −t_A )−(1/2)g(t_B ^2 −t_A ^2 )=h−h=0 u sin θ−(1/2)g(t_B +t_A )=0 ⇒t_B +t_A =((2u sin θ)/g) 2t_A =((2u sin θ)/g)−((2h)/(u cos θ)) ⇒t_A =((u sin θ)/g)−(h/(u cos θ)) u cos θ (((u sin θ)/g)−(h/(u cos θ)))=2h ⇒u^2 sin θ cos θ=3gh (u sin θ −(1/2)gt_A )t_A =h [u sin θ −(1/2)g(((u sin θ)/g)−(h/(u cos θ)))](((u sin θ)/g)−(h/(u cos θ)))=h (u sin θ +((gh)/(u cos θ)))(u sin θ−((gh)/(u cos θ)))=2gh u^2 sin^2 θ−((g^2 h^2 )/(u^2 cos^2 θ))=2gh (u^2 sin θ cos θ)^2 −g^2 h^2 =2ghu^2 cos^2 θ 9g^2 h^2 −g^2 h^2 =2ghu^2 cos^2 θ 4gh=u^2 cos^2 θ ⇒u cos θ=2(√(gh)) ⇒u sin θ=((3(√(gh)))/2) ⇒tan θ=(3/4) h_(max) at t=t_1 : u sin θ−gt_1 =0 t_1 =((u sin θ)/g)=((3(√(gh)))/(2g))=(3/2)(√(h/g)) h_(max) =u sin θ t_1 −(1/2)gt_1 ^2 =((3(√(gh)))/2)×(3/2)(√(h/g))−(1/2)g×(9/4)×(h/g) =((9h)/4)−((9h)/8)=((9h)/8) range at t=T (=period): u sin θ T−(1/2)gT^2 =0 ⇒T=((2 u sin θ)/g)=(2/g)×((3(√(gh)))/2)=3(√(h/g)) range R=u cos θ T=2(√(gh))×3(√(h/g))=6h u^2 =((3gh)/(sin θ cos θ))=((3gh)/((3/5)×(4/5)))=((25gh)/4)

$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${x}_{{A}} ={u}\:\mathrm{cos}\:\theta\:{t}_{{A}} =\mathrm{2}{h} \\ $$$${y}_{{A}} ={u}\:\mathrm{sin}\:\theta\:{t}_{{A}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{{A}} ^{\mathrm{2}} ={h} \\ $$$${x}_{{B}} ={u}\:\mathrm{cos}\:\theta\:{t}_{{B}} =\mathrm{4}{h} \\ $$$${y}_{{B}} ={u}\:\mathrm{sin}\:\theta\:{t}_{{B}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{{B}} ^{\mathrm{2}} ={h} \\ $$$${x}_{{B}} −{x}_{{A}} ={u}\:\mathrm{cos}\:\theta\:\left({t}_{{B}} −{t}_{{A}} \right)=\mathrm{4}{h}−\mathrm{2}{h}=\mathrm{2}{h} \\ $$$$\Rightarrow{t}_{{B}} −{t}_{{A}} =\frac{\mathrm{2}{h}}{{u}\:\mathrm{cos}\:\theta} \\ $$$${y}_{{B}} −{y}_{{B}} ={u}\:\mathrm{sin}\:\theta\:\left({t}_{{B}} −{t}_{{A}} \right)−\frac{\mathrm{1}}{\mathrm{2}}{g}\left({t}_{{B}} ^{\mathrm{2}} −{t}_{{A}} ^{\mathrm{2}} \right)={h}−{h}=\mathrm{0} \\ $$$${u}\:\mathrm{sin}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}{g}\left({t}_{{B}} +{t}_{{A}} \right)=\mathrm{0} \\ $$$$\Rightarrow{t}_{{B}} +{t}_{{A}} =\frac{\mathrm{2}{u}\:\mathrm{sin}\:\theta}{{g}} \\ $$$$\mathrm{2}{t}_{{A}} =\frac{\mathrm{2}{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{\mathrm{2}{h}}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow{t}_{{A}} =\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta} \\ $$$${u}\:\mathrm{cos}\:\theta\:\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\right)=\mathrm{2}{h} \\ $$$$\Rightarrow{u}^{\mathrm{2}} \mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{3}{gh} \\ $$$$\left({u}\:\mathrm{sin}\:\theta\:−\frac{\mathrm{1}}{\mathrm{2}}{gt}_{{A}} \right){t}_{{A}} ={h} \\ $$$$\left[{u}\:\mathrm{sin}\:\theta\:−\frac{\mathrm{1}}{\mathrm{2}}{g}\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\right)\right]\left(\frac{{u}\:\mathrm{sin}\:\theta}{{g}}−\frac{{h}}{{u}\:\mathrm{cos}\:\theta}\right)={h} \\ $$$$\left({u}\:\mathrm{sin}\:\theta\:+\frac{{gh}}{{u}\:\mathrm{cos}\:\theta}\right)\left({u}\:\mathrm{sin}\:\theta−\frac{{gh}}{{u}\:\mathrm{cos}\:\theta}\right)=\mathrm{2}{gh} \\ $$$${u}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta−\frac{{g}^{\mathrm{2}} {h}^{\mathrm{2}} }{{u}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}=\mathrm{2}{gh} \\ $$$$\left({u}^{\mathrm{2}} \mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} −{g}^{\mathrm{2}} {h}^{\mathrm{2}} =\mathrm{2}{ghu}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{9}{g}^{\mathrm{2}} {h}^{\mathrm{2}} −{g}^{\mathrm{2}} {h}^{\mathrm{2}} =\mathrm{2}{ghu}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{4}{gh}={u}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$$\Rightarrow{u}\:\mathrm{cos}\:\theta=\mathrm{2}\sqrt{{gh}} \\ $$$$\Rightarrow{u}\:\mathrm{sin}\:\theta=\frac{\mathrm{3}\sqrt{{gh}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$${h}_{{max}} \:{at}\:{t}={t}_{\mathrm{1}} : \\ $$$${u}\:\mathrm{sin}\:\theta−{gt}_{\mathrm{1}} =\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\frac{{u}\:\mathrm{sin}\:\theta}{{g}}=\frac{\mathrm{3}\sqrt{{gh}}}{\mathrm{2}{g}}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\frac{{h}}{{g}}} \\ $$$${h}_{{max}} ={u}\:\mathrm{sin}\:\theta\:{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{3}\sqrt{{gh}}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\frac{{h}}{{g}}}−\frac{\mathrm{1}}{\mathrm{2}}{g}×\frac{\mathrm{9}}{\mathrm{4}}×\frac{{h}}{{g}} \\ $$$$=\frac{\mathrm{9}{h}}{\mathrm{4}}−\frac{\mathrm{9}{h}}{\mathrm{8}}=\frac{\mathrm{9}{h}}{\mathrm{8}} \\ $$$$ \\ $$$${range}\:{at}\:{t}={T}\:\left(={period}\right): \\ $$$${u}\:\mathrm{sin}\:\theta\:{T}−\frac{\mathrm{1}}{\mathrm{2}}{gT}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{T}=\frac{\mathrm{2}\:{u}\:\mathrm{sin}\:\theta}{{g}}=\frac{\mathrm{2}}{{g}}×\frac{\mathrm{3}\sqrt{{gh}}}{\mathrm{2}}=\mathrm{3}\sqrt{\frac{{h}}{{g}}} \\ $$$${range}\:{R}={u}\:\mathrm{cos}\:\theta\:{T}=\mathrm{2}\sqrt{{gh}}×\mathrm{3}\sqrt{\frac{{h}}{{g}}}=\mathrm{6}{h} \\ $$$$ \\ $$$${u}^{\mathrm{2}} =\frac{\mathrm{3}{gh}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}=\frac{\mathrm{3}{gh}}{\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{5}}}=\frac{\mathrm{25}{gh}}{\mathrm{4}} \\ $$

Commented by mr W last updated on 03/May/20

we get exactly the same results as with method I.

$${we}\:{get}\:{exactly}\:{the}\:{same}\:{results}\:{as}\:{with} \\ $$$${method}\:{I}. \\ $$

Commented by Rio Michael last updated on 03/May/20

wow sir thank you so much for you effort in making me understand this particular problem you are such a God′s send. thank you so much sir. am 100% sure to solve any projectile problem like this.

$$\mathrm{wow}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{for}\:\mathrm{you}\:\mathrm{effort} \\ $$$$\mathrm{in}\:\mathrm{making}\:\mathrm{me}\:\mathrm{understand}\:\mathrm{this}\:\mathrm{particular}\:\mathrm{problem} \\ $$$$\mathrm{you}\:\mathrm{are}\:\mathrm{such}\:\mathrm{a}\:\mathrm{God}'\mathrm{s}\:\mathrm{send}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$$$\mathrm{am}\:\mathrm{100\%}\:\mathrm{sure}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{any}\:\mathrm{projectile}\:\mathrm{problem}\:\mathrm{like}\:\mathrm{this}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com