Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 91735 by frc2crc last updated on 02/May/20

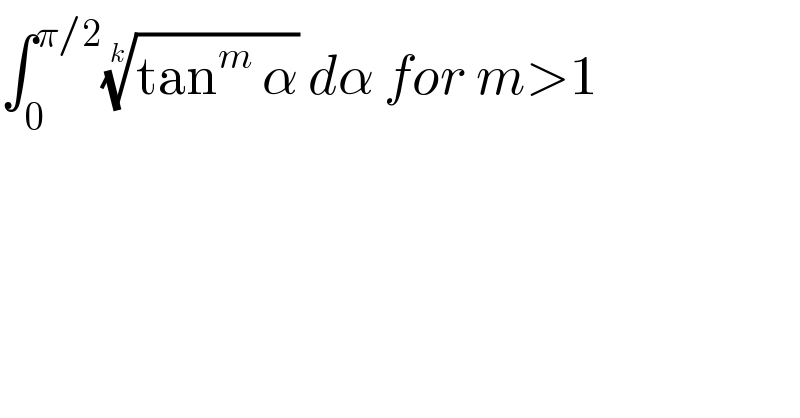
∫_0 ^(π/2) ((tan^m α))^(1/k) dα for m>1

$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \sqrt[{{k}}]{\mathrm{tan}^{{m}} \:\alpha}\:{d}\alpha\:{for}\:{m}>\mathrm{1} \\ $$

Commented bymathmax by abdo last updated on 03/May/20

I =∫_0 ^(π/2) (tan^m α)^(1/k) dα chsngement tanα =x give I =∫_0 ^∞ (x^m )^(1/k) (dx/(1+x^2 )) =∫_0 ^∞ (x^(m/k) /(1+x^2 ))dx changement x=u^(1/2) give I =∫_0 ^∞ (u^(m/(2k)) /(1+u)) (1/2)u^((1/2)−1) du =(1/2)∫_0 ^∞ (u^((m/(2k))+(1/2)−1) /(1+u)) du we have proved that ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) if o<a<1 ⇒ I =(1/2)×(π/(sin(π((m/(2k))+(1/2))))) =(π/(2sin(((mπ)/(2k))+(π/2)))) ⇒ I =(π/(2cos(((mπ)/(2k))))) (m/(2k))+(1/2)−1 =(m/(2k))−(1/2) =(1/2)((m/k)−1)<0 ⇒m<k so the condition is 1<m<k

$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({tan}^{{m}} \alpha\right)^{\frac{\mathrm{1}}{{k}}} \:{d}\alpha\:\:{chsngement}\:{tan}\alpha\:={x}\:{give} \\ $$ $${I}\:=\int_{\mathrm{0}} ^{\infty} \left({x}^{{m}} \right)^{\frac{\mathrm{1}}{{k}}} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{{m}}{{k}}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{changement}\:\:{x}={u}^{\frac{\mathrm{1}}{\mathrm{2}}} \:{give} \\ $$ $${I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{{m}}{\mathrm{2}{k}}} }{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{\mathrm{2}}{u}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{{m}}{\mathrm{2}{k}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du} \\ $$ $${we}\:{have}\:{proved}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:{if}\:{o}<{a}<\mathrm{1}\:\Rightarrow\: \\ $$ $${I}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{{sin}\left(\pi\left(\frac{{m}}{\mathrm{2}{k}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)}\:=\frac{\pi}{\mathrm{2}{sin}\left(\frac{{m}\pi}{\mathrm{2}{k}}+\frac{\pi}{\mathrm{2}}\right)}\:\Rightarrow \\ $$ $${I}\:=\frac{\pi}{\mathrm{2}{cos}\left(\frac{{m}\pi}{\mathrm{2}{k}}\right)} \\ $$ $$\frac{{m}}{\mathrm{2}{k}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\:=\frac{{m}}{\mathrm{2}{k}}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{m}}{{k}}−\mathrm{1}\right)<\mathrm{0}\:\Rightarrow{m}<{k}\:\:{so}\:{the}\:{condition}\:{is} \\ $$ $$\mathrm{1}<{m}<{k} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com