Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 91843 by jagoll last updated on 03/May/20

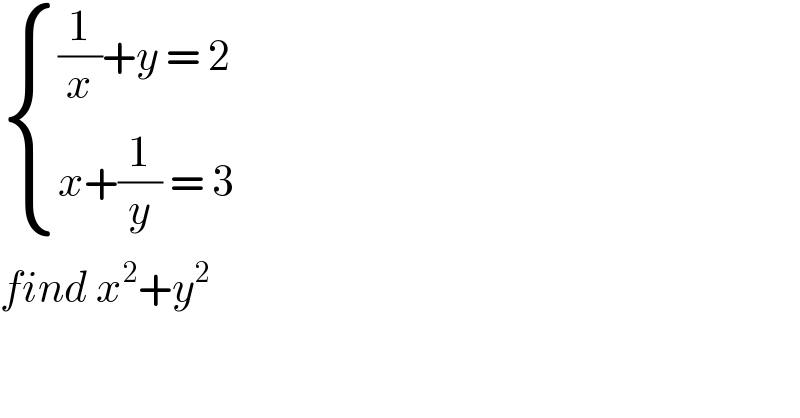
{ (((1/x)+y = 2)),((x+(1/y) = 3)) :} find x^2 +y^2

$$\begin{cases}{\frac{\mathrm{1}}{{x}}+{y}\:=\:\mathrm{2}}\\{{x}+\frac{\mathrm{1}}{{y}}\:=\:\mathrm{3}}\end{cases} \\ $$$${find}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$

Commented by jagoll last updated on 03/May/20

Commented by jagoll last updated on 03/May/20

��������

Commented by john santu last updated on 03/May/20

��������

Commented by Prithwish Sen 1 last updated on 03/May/20

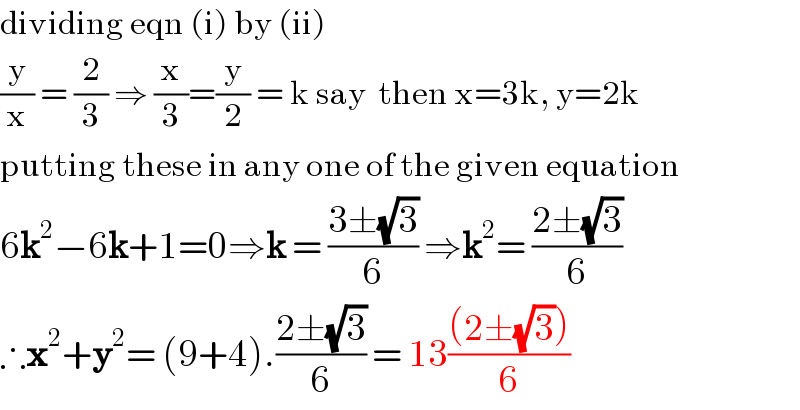
dividing eqn (i) by (ii) (y/x) = (2/3) ⇒ (x/3)=(y/2) = k say then x=3k, y=2k putting these in any one of the given equation 6k^2 −6k+1=0⇒k = ((3±(√3))/6) ⇒k^2 = ((2±(√3))/6) ∴x^2 +y^2 = (9+4).((2±(√3))/6) = 13(((2±(√3)))/6)

$$\mathrm{dividing}\:\mathrm{eqn}\:\left(\mathrm{i}\right)\:\mathrm{by}\:\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:\frac{\mathrm{x}}{\mathrm{3}}=\frac{\mathrm{y}}{\mathrm{2}}\:=\:\mathrm{k}\:\mathrm{say}\:\:\mathrm{then}\:\mathrm{x}=\mathrm{3k},\:\mathrm{y}=\mathrm{2k} \\ $$$$\mathrm{putting}\:\mathrm{these}\:\mathrm{in}\:\mathrm{any}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{6}\boldsymbol{\mathrm{k}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{\mathrm{k}}+\mathrm{1}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{k}}\:=\:\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{6}}\:\Rightarrow\boldsymbol{\mathrm{k}}^{\mathrm{2}} =\:\frac{\mathrm{2}\pm\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\therefore\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\:\left(\mathrm{9}+\mathrm{4}\right).\frac{\mathrm{2}\pm\sqrt{\mathrm{3}}}{\mathrm{6}}\:=\:\mathrm{13}\frac{\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)}{\mathrm{6}} \\ $$

Commented by jagoll last updated on 03/May/20

��✒️

Answered by mr W last updated on 03/May/20

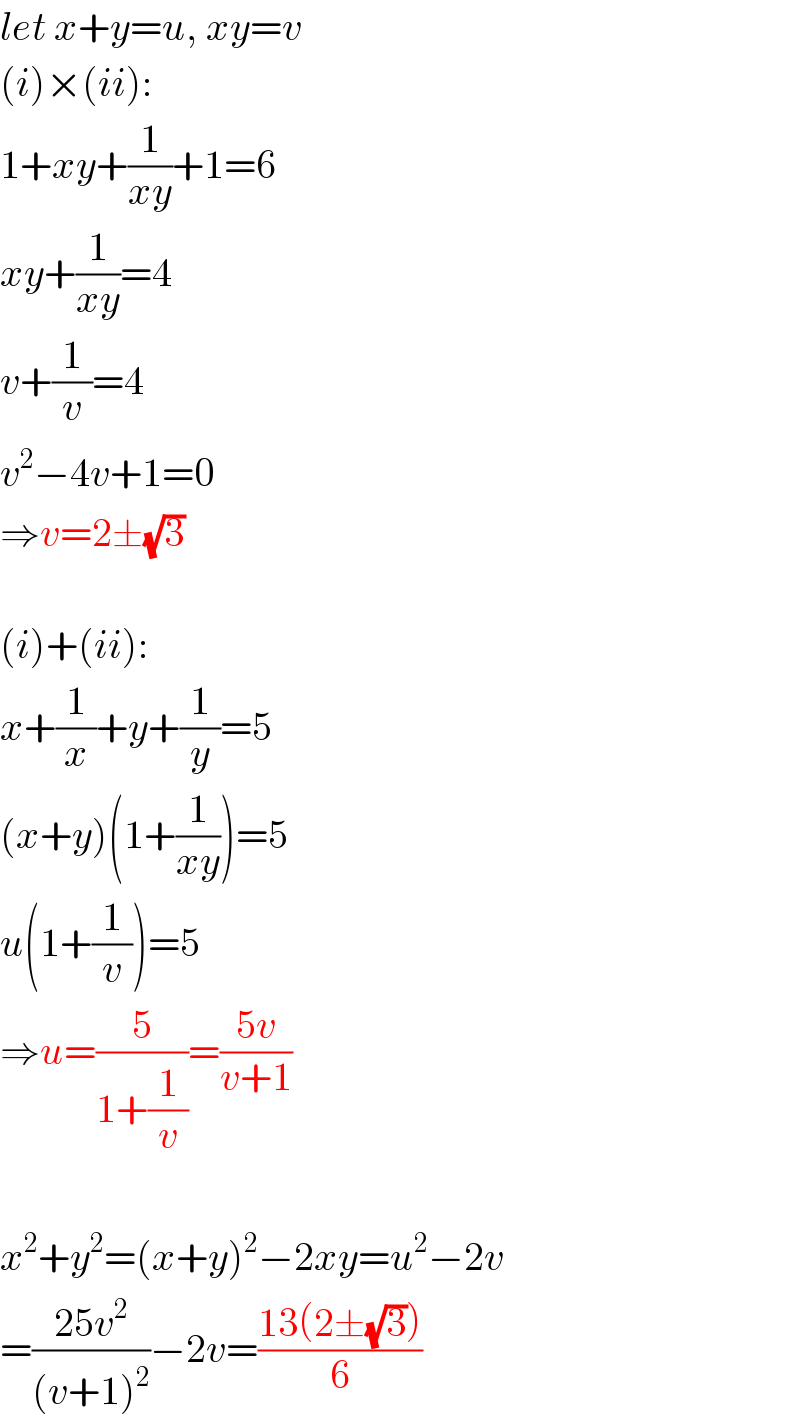
let x+y=u, xy=v (i)×(ii): 1+xy+(1/(xy))+1=6 xy+(1/(xy))=4 v+(1/v)=4 v^2 −4v+1=0 ⇒v=2±(√3) (i)+(ii): x+(1/x)+y+(1/y)=5 (x+y)(1+(1/(xy)))=5 u(1+(1/v))=5 ⇒u=(5/(1+(1/v)))=((5v)/(v+1)) x^2 +y^2 =(x+y)^2 −2xy=u^2 −2v =((25v^2 )/((v+1)^2 ))−2v=((13(2±(√3)))/6)

$${let}\:{x}+{y}={u},\:{xy}={v} \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\mathrm{1}+{xy}+\frac{\mathrm{1}}{{xy}}+\mathrm{1}=\mathrm{6} \\ $$$${xy}+\frac{\mathrm{1}}{{xy}}=\mathrm{4} \\ $$$${v}+\frac{\mathrm{1}}{{v}}=\mathrm{4} \\ $$$${v}^{\mathrm{2}} −\mathrm{4}{v}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{v}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${x}+\frac{\mathrm{1}}{{x}}+{y}+\frac{\mathrm{1}}{{y}}=\mathrm{5} \\ $$$$\left({x}+{y}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{xy}}\right)=\mathrm{5} \\ $$$${u}\left(\mathrm{1}+\frac{\mathrm{1}}{{v}}\right)=\mathrm{5} \\ $$$$\Rightarrow{u}=\frac{\mathrm{5}}{\mathrm{1}+\frac{\mathrm{1}}{{v}}}=\frac{\mathrm{5}{v}}{{v}+\mathrm{1}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}={u}^{\mathrm{2}} −\mathrm{2}{v} \\ $$$$=\frac{\mathrm{25}{v}^{\mathrm{2}} }{\left({v}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{2}{v}=\frac{\mathrm{13}\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)}{\mathrm{6}} \\ $$

Commented by jagoll last updated on 03/May/20

����

Answered by MJS last updated on 03/May/20

without thinking, without tricks: { ((1+xy=2x)),((1+xy=3y)) :} ⇒ y=(2/3)x ⇒ 2x^2 −6x+3=0 ⇒ x=((3±(√3))/2) ⇒ y=((3±(√3))/3)

$$\mathrm{without}\:\mathrm{thinking},\:\mathrm{without}\:\mathrm{tricks}: \\ $$$$\begin{cases}{\mathrm{1}+{xy}=\mathrm{2}{x}}\\{\mathrm{1}+{xy}=\mathrm{3}{y}}\end{cases}\:\Rightarrow\:{y}=\frac{\mathrm{2}}{\mathrm{3}}{x} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{3}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$

Commented by jagoll last updated on 03/May/20

��������������

Commented by Ar Brandon last updated on 03/May/20

�� Brilliant !

Terms of Service

Privacy Policy

Contact: info@tinkutara.com