Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 91910 by Ar Brandon last updated on 03/May/20

$$\int \frac{\ln (1+{\sin }^2\mathrm{x})}{{\sin }^2\mathrm{x}}\mathrm{dx}$$

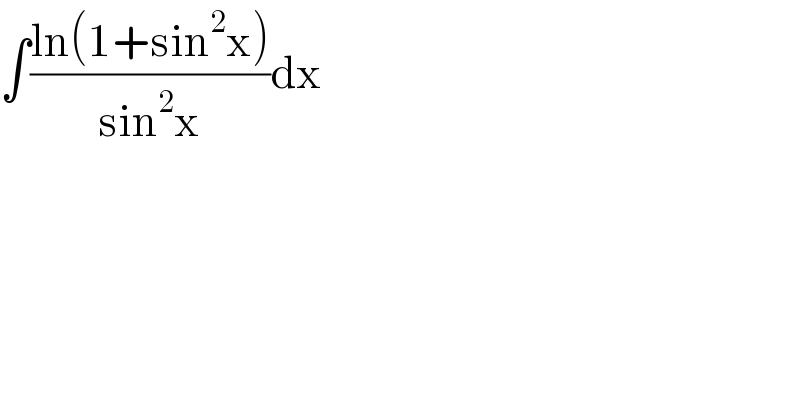
Commented by mathmax by abdo last updated on 03/May/20

$$letf\left(a\right)=\int \frac{ln(1+{asin}^{2}x)}{{sin}^{2}x}witha>0$$$$f^{{}^{\prime }}\left(a\right)=\int ln(1+{asin}^{2}x)dx=\int ln(1+a\times \frac{1-cos\left(2x\right)}{2})dx$$$$=\int ln(2+a-acos\left(2x\right))dx-xln\left(2\right)$$$$=\int ln((2+a)(1-\frac{a}{2+a}cos\left(2x\right))dx-xln\left(2\right)$$$$=(ln(2+a)-ln2)x+\int ln(1-\frac{a}{a+2}cos\left(2x\right))letdetermine$$$$I_{\lambda }=\int ln(1-\lambda cos\left(2x\right))dxwith0<\lambda <1$$$$\frac{{dI}_{\lambda }}{d\lambda }=-\int \frac{cos\left(2x\right)}{1-\lambda cos\left(2x\right)}dx{=}_{2x=t}\frac{1}{2}\int \frac{cos\left(t\right)}{1-\lambda cost}dt$$$$=-\frac{1}{2\lambda }\int \frac{1-\lambda cost-1}{1-\lambda cost}dt=-\frac{1}{2\lambda }t+\frac{1}{2\lambda }\int \frac{dt}{1-\lambda cost}$$$$\int \frac{dt}{1-\lambda cost}{=}_{tan\left(\frac{x}{2}\right)=u}\int \frac{2du}{(1+u^2)(1-\lambda \frac{1-u^2}{1+u^2})}$$$$=2\int \frac{du}{1+u^2-\lambda +\lambda u^2}=2\int \frac{du}{(1+\lambda )u^2+1-\lambda }$$$$=\frac{2}{1+\lambda }\int \frac{du}{u^2+\frac{1-\lambda }{1+\lambda }}{=}_{u=\sqrt{\frac{1-\lambda }{1+\lambda }}z}\frac{2}{1+\lambda }\int \frac{1}{\frac{1-\lambda }{1+\lambda }(1+z^2)}\times \frac{\sqrt{1-\lambda }}{\sqrt{1+\lambda }}dz$$$$=\frac{2}{\sqrt{1-{\lambda }^2}}\times \frac{\pi }{2}=\frac{\pi }{\sqrt{1-{\lambda }^2}}\Rightarrow I{}_{\lambda }^{\prime }=-\frac{x}{\lambda }+\frac{\pi }{2\lambda \sqrt{1-{\lambda }^2}}\Rightarrow$$$$I_{\lambda }=-xln\lambda +\frac{\pi }{2}\int \frac{d\lambda }{\lambda \sqrt{1-{\lambda }^2}}+C$$$$\int \frac{d\lambda }{\lambda \sqrt{1-{\lambda }^2}}{=}_{\lambda =sint}\int \frac{costdt}{sintcost}=\int \frac{dt}{sint}{=}_{tan\left(\frac{t}{2}\right)=u}$$$$=\int \frac{2du}{(1+u^2)\frac{2u}{1+u^2}}=\int \frac{du}{u}=ln\mid u\mid =ln\mid tan\left(\frac{arcsin\lambda }{2}\right)\mid \Rightarrow$$$$I_{\lambda }=-xln\lambda +\frac{\pi }{2}ln\mid tan\left(\frac{arcsin\lambda }{2}\right)\mid +C\Rightarrow$$$$f^{{}^{\prime }}\left(a\right)=xln\left(\frac{2+a}{2}\right)-xln\left(\frac{a}{a+2}\right)+\frac{\pi }{2}ln\mid tan\left(\frac{arcsin\left(\frac{a}{a+2}\right)}{2}\right)\mid +C$$$$\Rightarrow f\left(a\right)=x\int (ln\left(\frac{2+a}{2}\right)-ln\left(\frac{a}{a+2}\right)\mid +\frac{\pi }{2}\int ln\mid tan\left(\frac{arcsin\left(\frac{a}{a+2}\right)}{2}\right)+C$$$$....becontinued....$$

Commented by Ar Brandon last updated on 03/May/20

�� thanks

Commented by mathmax by abdo last updated on 03/May/20

$$youarewelcome$$

Commented by Ar Brandon last updated on 03/May/20

I got this. What do think ? ����

Commented by turbo msup by abdo last updated on 03/May/20

$$thisisthewaytheproblemehere$$$$isthstintegrsliswithoutlimits...$$

Answered by Ar Brandon last updated on 03/May/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com