Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 91936 by MWSuSon last updated on 03/May/20

$$howtoevaluateln\left(i\right),i=\sqrt{-1}.$$

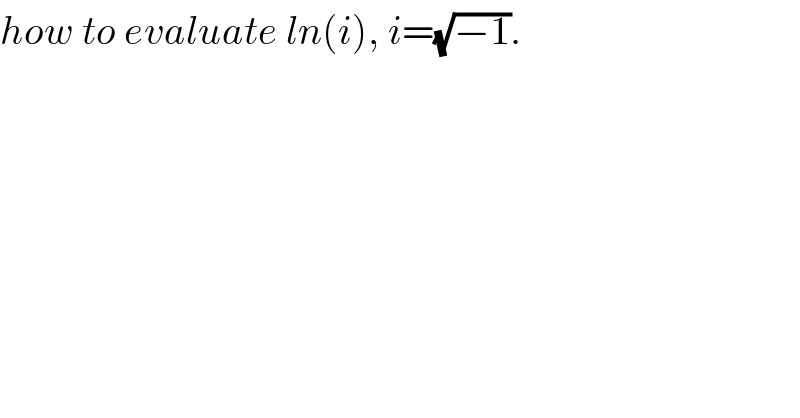
Commented by MWSuSon last updated on 03/May/20

thank you sir, but what if I'm looking for log(i) in base 2 or 10?

Commented by mr W last updated on 03/May/20

$${\log }_{10}\left(i\right)=\frac{\ln \left(i\right)}{\ln 10}=\frac{\pi }{2\ln 10}i$$$${\log }_2\left(i\right)=\frac{\ln \left(i\right)}{\ln 2}=\frac{\pi }{2\ln 2}i$$$$...$$

Commented by MWSuSon last updated on 03/May/20

oh I see, change of base. Thank you sir.

Commented by mr W last updated on 03/May/20

$$i=e^{\frac{\pi i}{2}}$$$$\ln \left(i\right)=\ln \left(e^{\frac{\pi i}{2}}\right)=\frac{\pi }{2}i$$

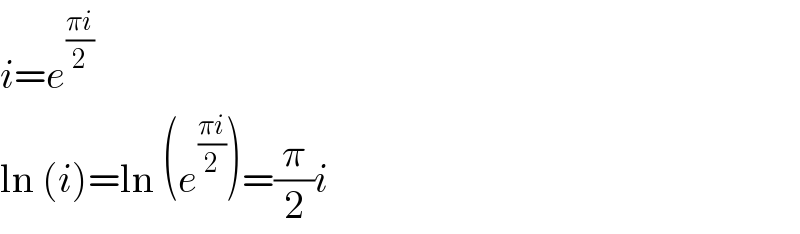
Commented by MWSuSon last updated on 03/May/20

$$sirsothesolutionofthisequation$$$$2^{(x+1)}=i$$$$wouldproceedasfollows?$$$$x+1={log}_{2}i$$$$x={log}_{2}i-1$$$$x=\frac{lni}{ln2}-1$$$$x=\frac{\pi }{2ln2}i-1?$$$$$$

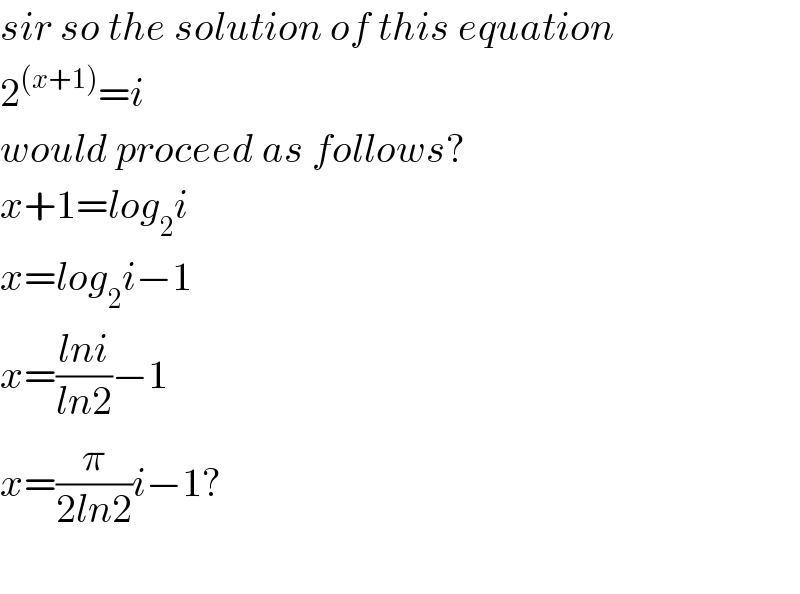
Commented by mr W last updated on 04/May/20

$$yes$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com