
Question and Answers Forum
Question Number 92003 by zainal tanjung last updated on 04/May/20
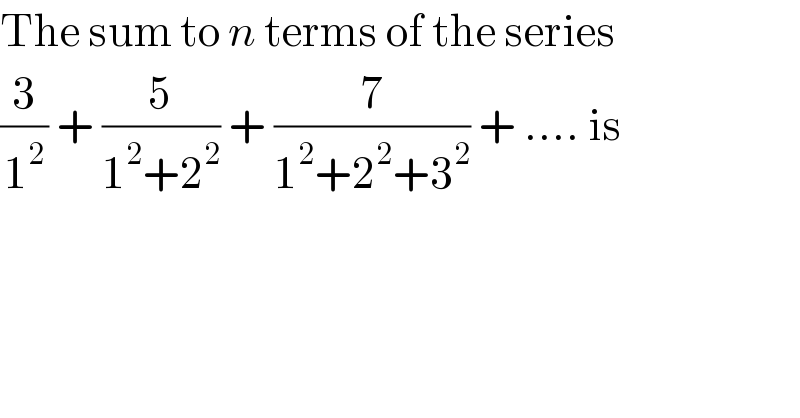
Commented by Prithwish Sen 1 last updated on 04/May/20
![t_(n ) = ((6(2n+1))/(n(n+1)(2n+1))) = 6[(1/n)−(1/(n+1))] now the series becomes lim_(k→∞) 6[Σ_(n=1) ^k ((1/n)−(1/(n+1)))] = lim_(k→∞) 6[(k/(k+1))]= lim_(k→∞) 6.(1/(1+(1/k))) = 6.1 = 6 please check](Q92011.png)
Commented by mathmax by abdo last updated on 04/May/20
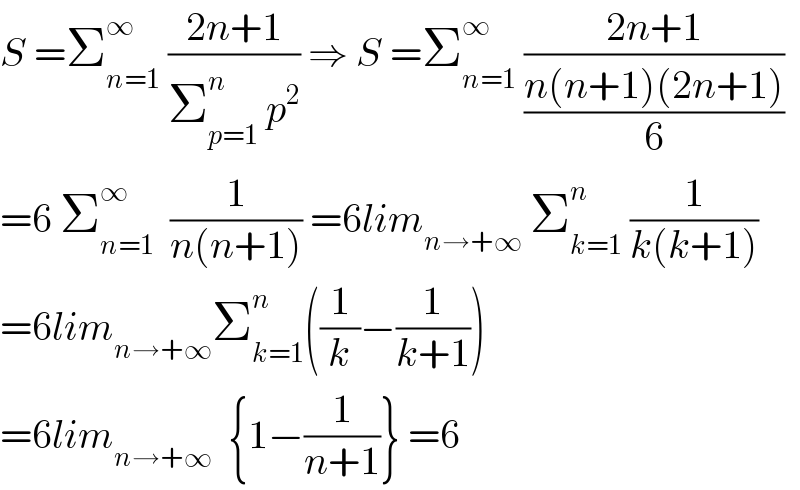
| ||
Question and Answers Forum | ||
Question Number 92003 by zainal tanjung last updated on 04/May/20 | ||
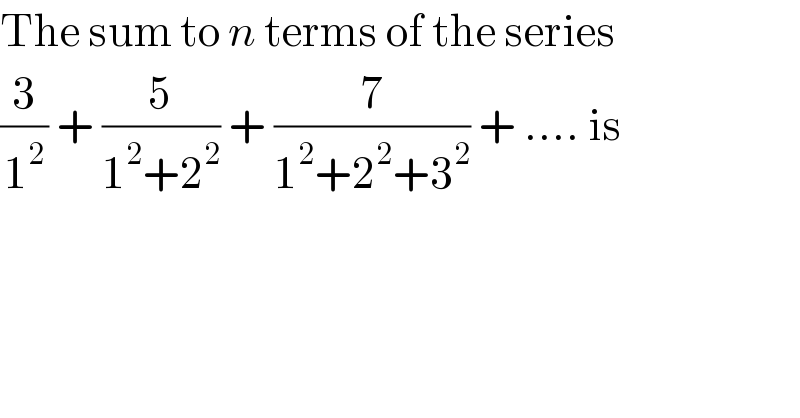 | ||
Commented by Prithwish Sen 1 last updated on 04/May/20 | ||
![t_(n ) = ((6(2n+1))/(n(n+1)(2n+1))) = 6[(1/n)−(1/(n+1))] now the series becomes lim_(k→∞) 6[Σ_(n=1) ^k ((1/n)−(1/(n+1)))] = lim_(k→∞) 6[(k/(k+1))]= lim_(k→∞) 6.(1/(1+(1/k))) = 6.1 = 6 please check](Q92011.png) | ||
Commented by mathmax by abdo last updated on 04/May/20 | ||
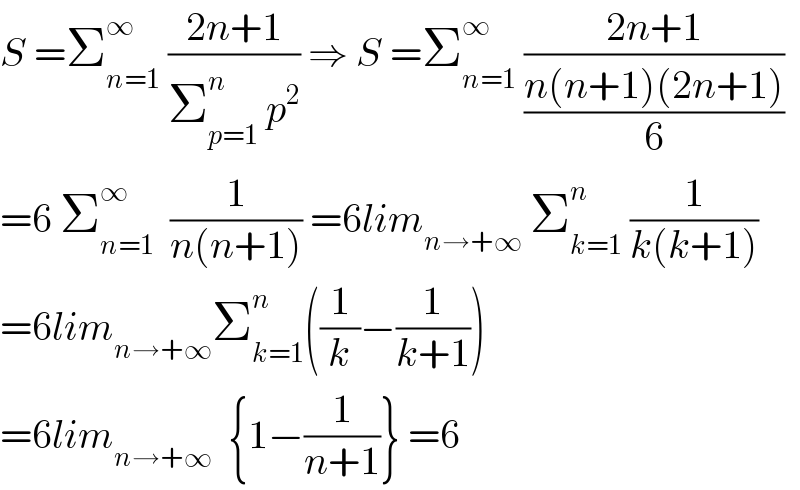 | ||