
Question and Answers Forum
Question Number 92025 by 675480065 last updated on 04/May/20
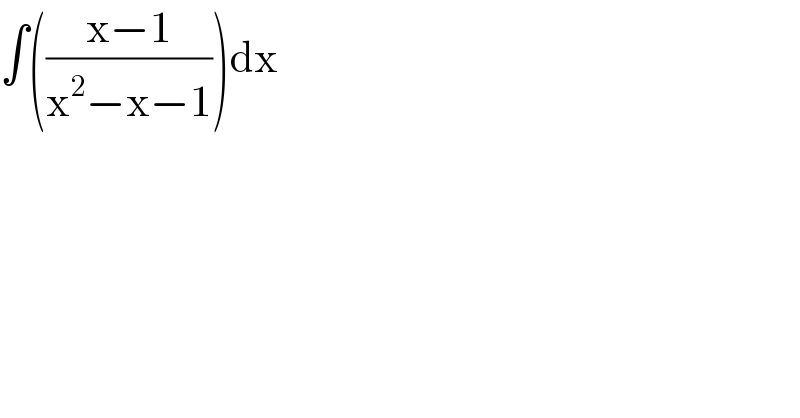
Commented by mathmax by abdo last updated on 04/May/20

Answered by niroj last updated on 04/May/20
![∫ (( x−1)/(x^2 −x−1))dx= (1/2)∫ ((2x−1−1)/(x^2 −x−1))dx = (1/2)∫ ((2x−1)/(x^2 −x−1))dx−(1/2)∫ (( 1)/(x^2 −x−1))dx = (1/2)log (x^2 −x−1)+ (1/2)∫ (( 1)/(x^2 −2x.(1/2)+(1/4)−(1/4)−1))dx +C = log (x^2 −x−1)^(1/2) +(1/2) ∫ (( 1)/((x−(1/2))^2 −(((√5)/2))^2 ))dx+C = log(√(x^2 −x−1)) + (1/2)[ (1/(2.((√5)/2)))log ((x−(1/2) −((√5)/2))/(x−(1/2) +((√5)/2)))]+C = log(√(x^2 −x−1)) +(1/(2(√5)))log ((2x−1−(√5))/(2x−1+(√5))) +C = log(√(x^2 −x−1)) + ((√5)/(10))log ((2x−1−(√5))/(2x−1+(√5))) +C //.](Q92034.png)
Answered by MJS last updated on 04/May/20
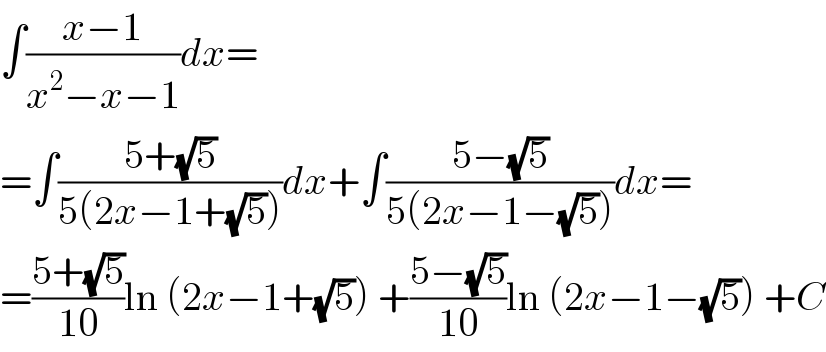
| ||
Question and Answers Forum | ||
Question Number 92025 by 675480065 last updated on 04/May/20 | ||
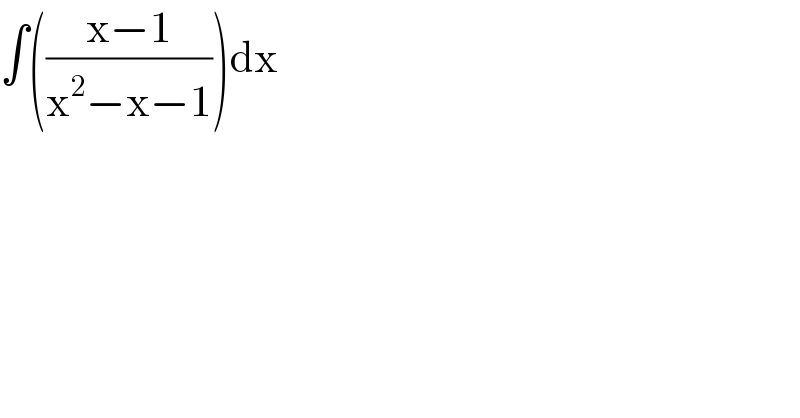 | ||
Commented by mathmax by abdo last updated on 04/May/20 | ||
 | ||
Answered by niroj last updated on 04/May/20 | ||
![∫ (( x−1)/(x^2 −x−1))dx= (1/2)∫ ((2x−1−1)/(x^2 −x−1))dx = (1/2)∫ ((2x−1)/(x^2 −x−1))dx−(1/2)∫ (( 1)/(x^2 −x−1))dx = (1/2)log (x^2 −x−1)+ (1/2)∫ (( 1)/(x^2 −2x.(1/2)+(1/4)−(1/4)−1))dx +C = log (x^2 −x−1)^(1/2) +(1/2) ∫ (( 1)/((x−(1/2))^2 −(((√5)/2))^2 ))dx+C = log(√(x^2 −x−1)) + (1/2)[ (1/(2.((√5)/2)))log ((x−(1/2) −((√5)/2))/(x−(1/2) +((√5)/2)))]+C = log(√(x^2 −x−1)) +(1/(2(√5)))log ((2x−1−(√5))/(2x−1+(√5))) +C = log(√(x^2 −x−1)) + ((√5)/(10))log ((2x−1−(√5))/(2x−1+(√5))) +C //.](Q92034.png) | ||
| ||
Answered by MJS last updated on 04/May/20 | ||
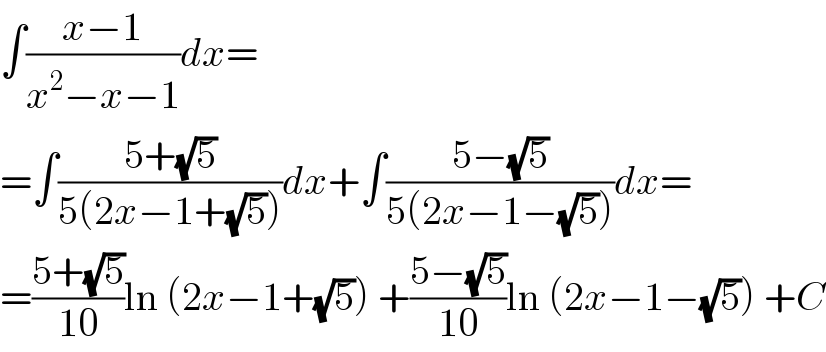 | ||
| ||