Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 92102 by  M±th+et+s last updated on 04/May/20

$$howcanwefactorize{x}^5-1?$$

Commented by mathmax by abdo last updated on 05/May/20

$$complexmethod{z}^5=1withz={re}^{i\theta }\Rightarrow r^5{e}^{i5\theta }=e^{i2k\pi }\Rightarrow$$$$r=1and{\theta }_k=\frac{2k\pi }{5}k\in \left[[0,4]\right]sotherootsare{z}_k=e^{i\frac{2k\pi }{5}}$$$$z_0=1,z_1=e^{\frac{i2\pi }{5}},z_2=e^{i\frac{4\pi }{5}},z_3=e^{i\frac{6\pi }{5}},z_4=e^{i\frac{8\pi }{5}}$$$$wesee{\stackrel{-}{z}}_1=e^{-\frac{k2\pi }{5}}=z_{4}and{\stackrel{-}{z}}_2=z_3\Rightarrow$$$$z^5-1=\prod _{k=0}^4(z-z_k)=(z-1)(z-z_1)(z-{\stackrel{-}{z}}_1)(z-z_2)(z-{\stackrel{-}{z}}_2)$$$$=(z-1)(z^2-2Re\left(z_1\right)z+1)(z^2-2Re\left(z_2\right)z+1)\Rightarrow$$$$x^5-1=(x-1)(x^2-2cos\left(\frac{2\pi }{5}\right)x+1)(x^2-2cos\left(\frac{4\pi }{5}\right)x+1)$$$$wehavecos\left(\frac{4\pi }{5}\right)=-cos\left(\frac{\pi }{5}\right)=-\frac{1+\sqrt{5}}{4}$$$$cos\left(\frac{2\pi }{5}\right)=2{cos}^2\left(\frac{\pi }{5}\right)-1=2\times {\left(\frac{1+\sqrt{5}}{4}\right)}^2-1$$$$=\frac{1}{8}(6+2\sqrt{5})-1=\frac{6+2\sqrt{5}-8}{8}=\frac{-2+2\sqrt{5}}{8}=\frac{-1+\sqrt{5}}{4}\Rightarrow$$$$x^5-1=(x-1)(x^2-\frac{-1+\sqrt{5}}{2}x+1)(x^2+\frac{1+\sqrt{5}}{2}x+1)\Rightarrow$$$$x^5-1=(x-1)(x^2+\frac{1-\sqrt{5}}{2}x+1)(x^2+\frac{1+\sqrt{5}}{2}x+1)$$$$$$

Commented by  M±th+et+s last updated on 05/May/20

$$iamspeachless.godblessyousir$$

Commented by mathmax by abdo last updated on 06/May/20

$$youarewelcomesir.$$

Answered by niroj last updated on 04/May/20

$${\mathrm{x}}^6-1={\left({\mathrm{x}}^3\right)}^2-{\left(1\right)}^2$$$$=({\mathrm{x}}^3+1)({\mathrm{x}}^3-1)$$$$=(\mathrm{x}+1)({\mathrm{x}}^2-\mathrm{x}+1)(\mathrm{x}-1)({\mathrm{x}}^2+\mathrm{x}+1)$$$$=({\mathrm{x}}^2-1)({\mathrm{x}}^2+1-\mathrm{x})({\mathrm{x}}^2+1+\mathrm{x})$$$$=({\mathrm{x}}^2-1)\{{({\mathrm{x}}^2+1)}^2-{\left(\mathrm{x}\right)}^2\}$$$$=({\mathrm{x}}^2-1)({\mathrm{x}}^4+{2\mathrm{x}}^2+1-{\mathrm{x}}^2)$$$$=({\mathrm{x}}^2-1)({\mathrm{x}}^4+{\mathrm{x}}^2+1)//.$$

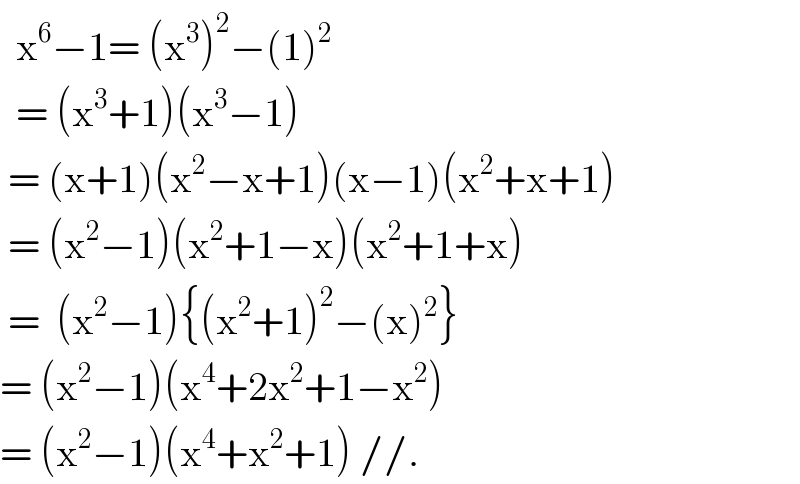
Commented by MJS last updated on 04/May/20

$$\mathrm{right}.\mathrm{but}{\mathrm{it}}^{\prime }\mathrm{s}\mathrm{better}\mathrm{to}\mathrm{have}\mathrm{square}\mathrm{factors}$$$$=(x^2-1)(x^2-x+1)(x^2+x+1)$$

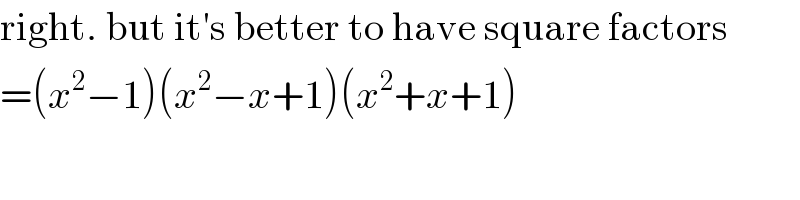
Commented by niroj last updated on 04/May/20

������

Commented by john santu last updated on 05/May/20

����

Answered by niroj last updated on 04/May/20

$${\mathrm{x}}^5-1=(\mathrm{x}-1)({\mathrm{x}}^4+{\mathrm{x}}^3+{\mathrm{x}}^2+\mathrm{x}+1)$$$$=\mathrm{x}({\mathrm{x}}^4+{\mathrm{x}}^3+{\mathrm{x}}^2+\mathrm{x}+1)-1({\mathrm{x}}^4+{\mathrm{x}}^3+{\mathrm{x}}^2+\mathrm{x}+1)$$$$={\mathrm{x}}^5+{\mathrm{x}}^4+{\mathrm{x}}^3+{\mathrm{x}}^2+\mathrm{x}-{\mathrm{x}}^4-{\mathrm{x}}^3-{\mathrm{x}}^2-\mathrm{x}-1$$$$={\mathrm{x}}^5-1//.$$

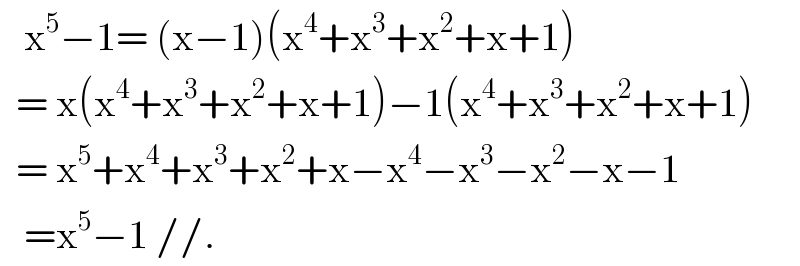
Commented by niroj last updated on 04/May/20

��

Commented by  M±th+et+s last updated on 04/May/20

$$thankyousir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com