
Question and Answers Forum
Question Number 92156 by abdomathmax last updated on 05/May/20
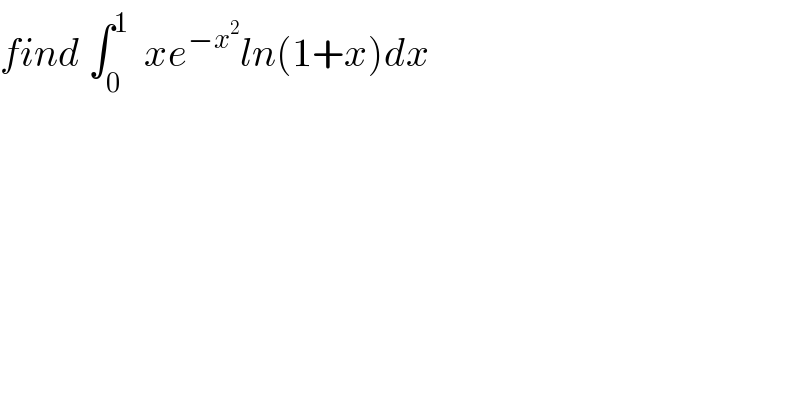
Commented by mathmax by abdo last updated on 08/May/20
![I =∫_0 ^1 x e^(−x^2 ) ln(1+x)dx by psrts I =[−(1/2)e^(−x^2 ) ln(1+x)]_0 ^1 +(1/2)∫_0 ^1 (e^(−x^2 ) /(1+x))dx =−(1/2)e^(−1) ln(2)+(1/2)∫_0 ^1 (e^(−x^2 ) /(1+x))dx ∫_0 ^1 (e^(−x^2 ) /(1+x))dx =_(1+x=t) ∫_1 ^2 (e^(−(t−1)^2 ) /t)dt =∫_1 ^2 (e^(−t^2 +2t −1) /t)dt =e^(−1) ∫_1 ^2 (e^(−t^2 +2t) /t) dt =e^(−1) ∫_1 ^2 (1/t)Σ_(n=0) ^∞ (((−t^2 +2t)^n )/(n!))dt =e^(−1) ∫_1 ^2 ((1/t)+(1/t)Σ_(n=1) ^∞ (((−t^2 +2t)^n )/(n!)))dt =e^(−1) ln(2) +e^(−1) Σ_(n=1) ^∞ ∫_1 ^2 ((t^(n−1) (2−t)^n )/(n!))dt ⇒ I = (1/(2e))Σ_(n=1) ^∞ (A_n /(n!)) with A_n =∫_1 ^2 t^(n−1) (2−t)^n dt ....be continued...](Q92715.png)
| ||
Question and Answers Forum | ||
Question Number 92156 by abdomathmax last updated on 05/May/20 | ||
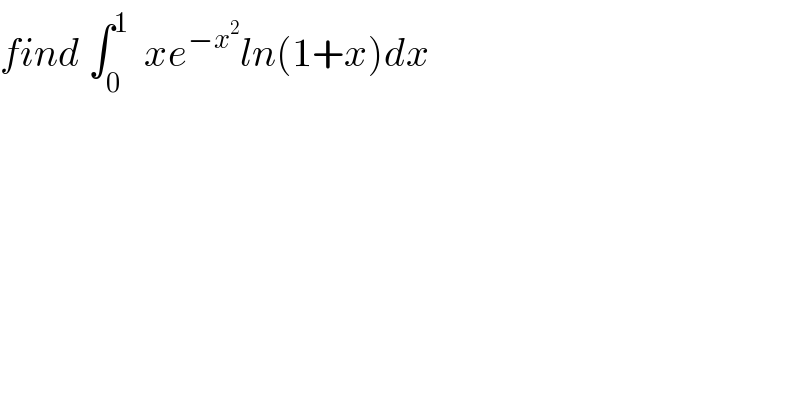 | ||
Commented by mathmax by abdo last updated on 08/May/20 | ||
![I =∫_0 ^1 x e^(−x^2 ) ln(1+x)dx by psrts I =[−(1/2)e^(−x^2 ) ln(1+x)]_0 ^1 +(1/2)∫_0 ^1 (e^(−x^2 ) /(1+x))dx =−(1/2)e^(−1) ln(2)+(1/2)∫_0 ^1 (e^(−x^2 ) /(1+x))dx ∫_0 ^1 (e^(−x^2 ) /(1+x))dx =_(1+x=t) ∫_1 ^2 (e^(−(t−1)^2 ) /t)dt =∫_1 ^2 (e^(−t^2 +2t −1) /t)dt =e^(−1) ∫_1 ^2 (e^(−t^2 +2t) /t) dt =e^(−1) ∫_1 ^2 (1/t)Σ_(n=0) ^∞ (((−t^2 +2t)^n )/(n!))dt =e^(−1) ∫_1 ^2 ((1/t)+(1/t)Σ_(n=1) ^∞ (((−t^2 +2t)^n )/(n!)))dt =e^(−1) ln(2) +e^(−1) Σ_(n=1) ^∞ ∫_1 ^2 ((t^(n−1) (2−t)^n )/(n!))dt ⇒ I = (1/(2e))Σ_(n=1) ^∞ (A_n /(n!)) with A_n =∫_1 ^2 t^(n−1) (2−t)^n dt ....be continued...](Q92715.png) | ||