
Question and Answers Forum
Question Number 92397 by john santu last updated on 06/May/20
![∫ (1/(x−(√(1−x^2 )))) dx [ x = sin w ] ∫ ((cos w dw)/(sin w−cos w)) = ∫ (dw/(tan w−1)) = ∫ ((sec^2 w dw)/((tan w−1)sec^2 w)) = ∫ (du/((u−1)(u^2 +1))) ; [ u = tan w ] = ∫ (du/(2(u−1)))−∫ ((u du )/(2(u^2 +1))) = (1/2)ln ∣u−1∣ −(1/4)ln∣u^2 +1∣ −(1/2)tan^(−1) (u) +c = (1/2)ln∣tan w−1∣−(1/4)ln∣tan^2 w+1∣− (1/2) tan^(−1) (tan w) +c = (1/2)ln∣(x/(√(1−x^2 )))−1∣+(1/4)ln∣1−x^2 ∣− (1/2)sin^(−1) (x) + c](Q92397.png)
Commented by abdomathmax last updated on 07/May/20
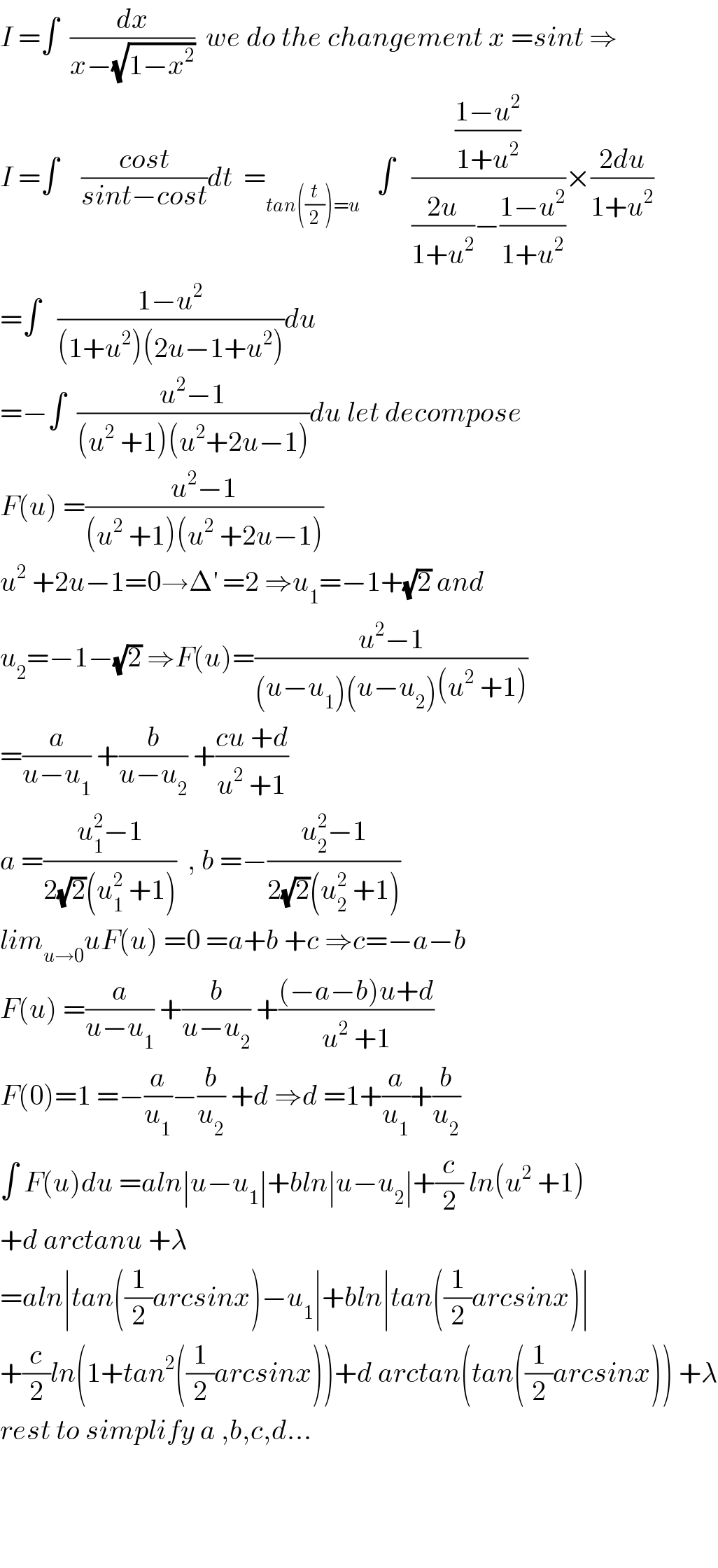
Commented by john santu last updated on 07/May/20
��������
| ||
Question and Answers Forum | ||
Question Number 92397 by john santu last updated on 06/May/20 | ||
![∫ (1/(x−(√(1−x^2 )))) dx [ x = sin w ] ∫ ((cos w dw)/(sin w−cos w)) = ∫ (dw/(tan w−1)) = ∫ ((sec^2 w dw)/((tan w−1)sec^2 w)) = ∫ (du/((u−1)(u^2 +1))) ; [ u = tan w ] = ∫ (du/(2(u−1)))−∫ ((u du )/(2(u^2 +1))) = (1/2)ln ∣u−1∣ −(1/4)ln∣u^2 +1∣ −(1/2)tan^(−1) (u) +c = (1/2)ln∣tan w−1∣−(1/4)ln∣tan^2 w+1∣− (1/2) tan^(−1) (tan w) +c = (1/2)ln∣(x/(√(1−x^2 )))−1∣+(1/4)ln∣1−x^2 ∣− (1/2)sin^(−1) (x) + c](Q92397.png) | ||
Commented by abdomathmax last updated on 07/May/20 | ||
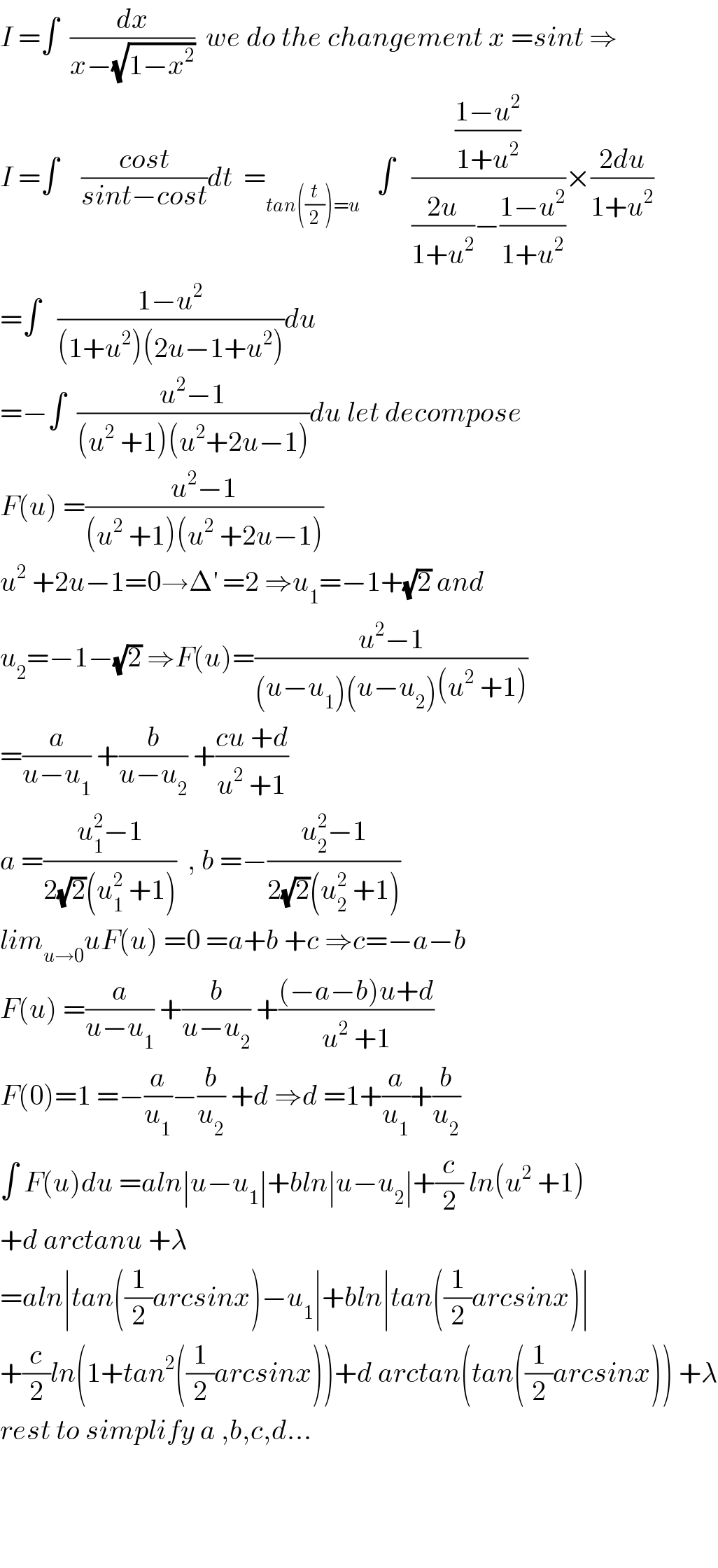 | ||
Commented by john santu last updated on 07/May/20 | ||
�������� | ||