Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 92605 by som(math1967) last updated on 08/May/20

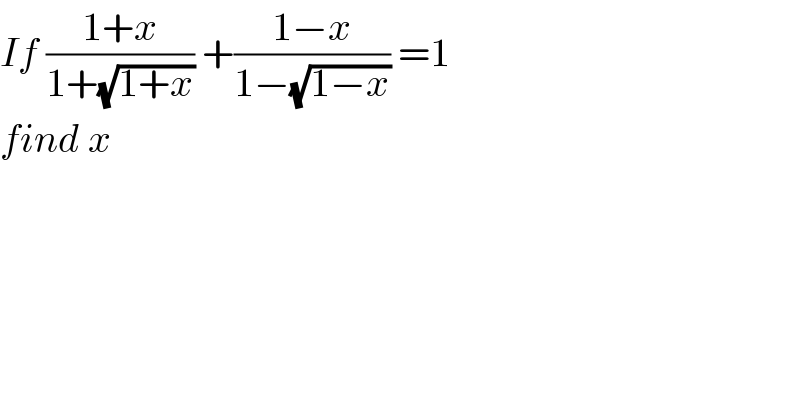
If ((1+x)/(1+(√(1+x)))) +((1−x)/(1−(√(1−x)))) =1 find x

$${If}\:\frac{\mathrm{1}+{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}}}\:+\frac{\mathrm{1}−{x}}{\mathrm{1}−\sqrt{\mathrm{1}−{x}}}\:=\mathrm{1} \\ $$$${find}\:{x} \\ $$

Commented by behi83417@gmail.com last updated on 08/May/20

(((1+x)(1−(√(1+x))))/(−x))+(((1−x)(1+(√(1−x))))/x)=1 ⇒(1+x)(√(1+x))−(1+x)+(1−x)(√(1−x))+(1−x)=x ⇒(1+x)(√(1+x))+(1−x)(√(1−x))=3x (−1<x<1,x≠0,let:x=cos2t)⇒ 2c^2 .(√2)c+2s^2 .(√2)s=3(c^2 −s^2 ) ⇒2(√2)(c^3 +s^3 )=3(c^2 −s^2 ) ⇒2(√2)(c+s)(c^2 +s^2 −cs)=3(c+s)(c−s) 1.c+s=0⇒(√2)cos(t−(π/4))=0⇒t=(π/4)(≡x=0:not ok) ⇒2(√2)(1−cs)=3(c−s) ⇒8(1−2cs+c^2 s^2 )=9(c^2 +s^2 −2cs) ⇒8c^2 s^2 +2cs−1=0 ⇒cs=((−1±(√(1+8)))/8)=(1/4),−(1/2) 1. cs=(1/4)⇒sin2t=(1/2)⇒x=cos2t=((√3)/2) 2. cs=−(1/2)⇒sin2t=−1⇒x=cos2t=0 [not ok]

$$\frac{\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{x}}\right)}{−\mathrm{x}}+\frac{\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}}\right)}{\mathrm{x}}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}}−\left(\mathrm{1}+\mathrm{x}\right)+\left(\mathrm{1}−\mathrm{x}\right)\sqrt{\mathrm{1}−\mathrm{x}}+\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{x} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}}+\left(\mathrm{1}−\mathrm{x}\right)\sqrt{\mathrm{1}−\mathrm{x}}=\mathrm{3x} \\ $$$$\left(−\mathrm{1}<\mathrm{x}<\mathrm{1},\mathrm{x}\neq\mathrm{0},\mathrm{let}:\mathrm{x}=\mathrm{cos2t}\right)\Rightarrow \\ $$$$\mathrm{2c}^{\mathrm{2}} .\sqrt{\mathrm{2}}\mathrm{c}+\mathrm{2s}^{\mathrm{2}} .\sqrt{\mathrm{2}}\mathrm{s}=\mathrm{3}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{s}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{c}^{\mathrm{3}} +\mathrm{s}^{\mathrm{3}} \right)=\mathrm{3}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{s}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{c}+\mathrm{s}\right)\left(\mathrm{c}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} −\mathrm{cs}\right)=\mathrm{3}\left(\mathrm{c}+\mathrm{s}\right)\left(\mathrm{c}−\mathrm{s}\right) \\ $$$$\mathrm{1}.\mathrm{c}+\mathrm{s}=\mathrm{0}\Rightarrow\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{t}−\frac{\pi}{\mathrm{4}}\right)=\mathrm{0}\Rightarrow\mathrm{t}=\frac{\pi}{\mathrm{4}}\left(\equiv\mathrm{x}=\mathrm{0}:\mathrm{not}\:\mathrm{ok}\right) \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{cs}\right)=\mathrm{3}\left(\mathrm{c}−\mathrm{s}\right) \\ $$$$\Rightarrow\mathrm{8}\left(\mathrm{1}−\mathrm{2cs}+\mathrm{c}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \right)=\mathrm{9}\left(\mathrm{c}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} −\mathrm{2cs}\right) \\ $$$$\Rightarrow\mathrm{8c}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{2cs}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cs}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8}}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{4}},−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}.\:\:\:\mathrm{cs}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{sin2t}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\boldsymbol{\mathrm{x}}=\mathrm{cos2t}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{2}.\:\:\:\mathrm{cs}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{sin2t}=−\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{cos2t}=\mathrm{0}\:\left[\mathrm{not}\:\mathrm{ok}\right] \\ $$

Commented by Tony Lin last updated on 08/May/20

let (√(1+x))=a,(√(1−x))=b,a^2 +b^2 =2 (a^2 /(1+a))+(b^2 /(1−b))=1 a^2 −a^2 b+b^2 +ab^2 =1+a−b−ab 1−ab(a−b)−(a−b)+ab=0 (1+ab)[1−(a−b)]=0 a−b=1 or ab=−1(false) (√(1+x))−(√(1−x))=1 1+x=(1+(√(1−x)))^2 2x−1=2(√(1−x)) 4x^2 −4x+1=4−4x x^2 =(3/4) x=±((√3)/2) but ((1−((√3)/2))/(1+(√(1−((√3)/2)))))+((1+((√3)/2))/(1−(√(1+((√3)/2)))))<0 (−5) ∴x=((√3)/2)

$${let}\:\sqrt{\mathrm{1}+{x}}={a},\sqrt{\mathrm{1}−{x}}={b},{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}}+\frac{{b}^{\mathrm{2}} }{\mathrm{1}−{b}}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}+{b}^{\mathrm{2}} +{ab}^{\mathrm{2}} =\mathrm{1}+{a}−{b}−{ab} \\ $$$$\mathrm{1}−{ab}\left({a}−{b}\right)−\left({a}−{b}\right)+{ab}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{ab}\right)\left[\mathrm{1}−\left({a}−{b}\right)\right]=\mathrm{0} \\ $$$${a}−{b}=\mathrm{1}\:{or}\:{ab}=−\mathrm{1}\left({false}\right) \\ $$$$\sqrt{\mathrm{1}+{x}}−\sqrt{\mathrm{1}−{x}}=\mathrm{1} \\ $$$$\mathrm{1}+{x}=\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{x}−\mathrm{1}=\mathrm{2}\sqrt{\mathrm{1}−{x}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{4}−\mathrm{4}{x} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${x}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${but}\:\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}}+\frac{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{1}−\sqrt{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}}<\mathrm{0}\:\left(−\mathrm{5}\right) \\ $$$$\therefore{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 08/May/20

Thanks sir

$${Thanks}\:{sir} \\ $$

Commented by som(math1967) last updated on 08/May/20

Thanks sir

$${Thanks}\:{sir} \\ $$

Answered by MJS last updated on 08/May/20

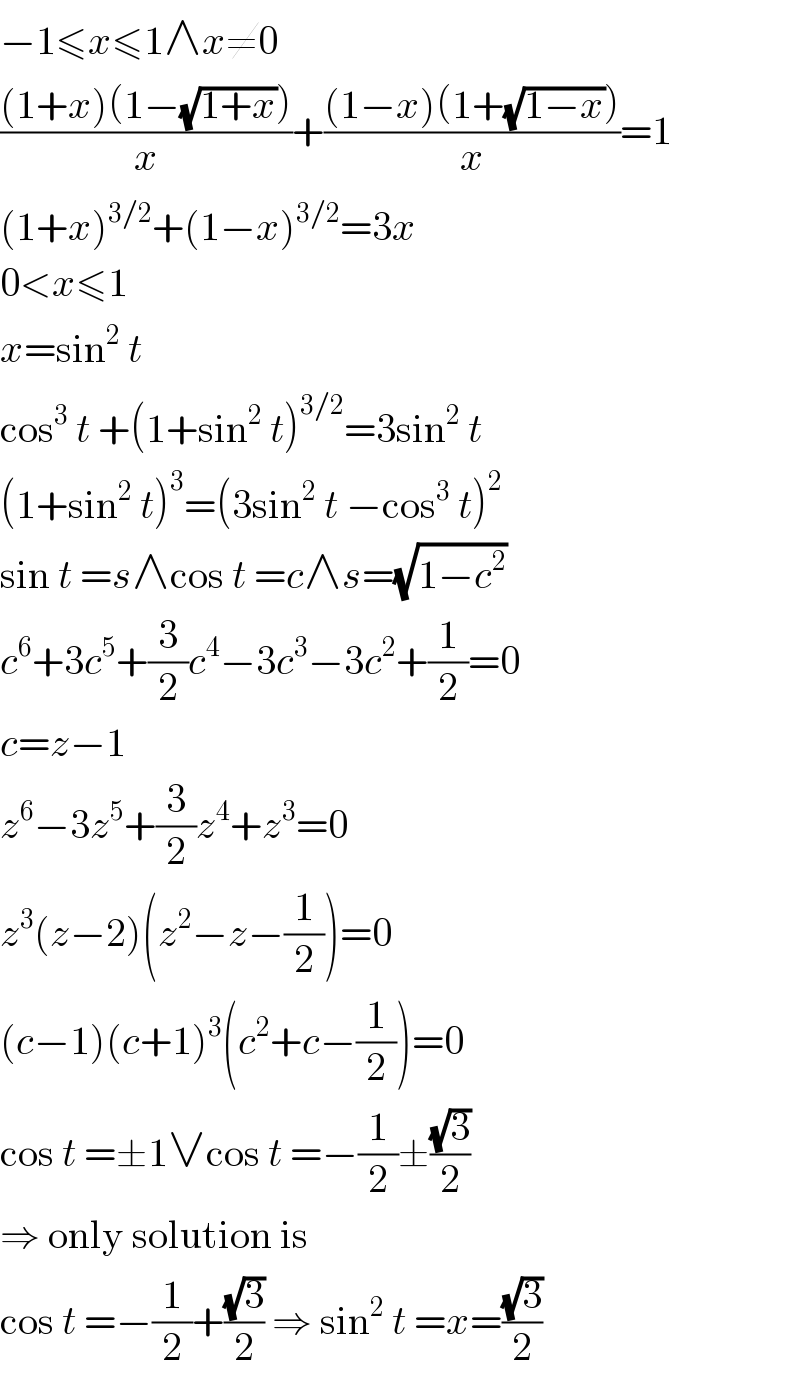
−1≤x≤1∧x≠0 (((1+x)(1−(√(1+x))))/x)+(((1−x)(1+(√(1−x))))/x)=1 (1+x)^(3/2) +(1−x)^(3/2) =3x 0<x≤1 x=sin^2 t cos^3 t +(1+sin^2 t)^(3/2) =3sin^2 t (1+sin^2 t)^3 =(3sin^2 t −cos^3 t)^2 sin t =s∧cos t =c∧s=(√(1−c^2 )) c^6 +3c^5 +(3/2)c^4 −3c^3 −3c^2 +(1/2)=0 c=z−1 z^6 −3z^5 +(3/2)z^4 +z^3 =0 z^3 (z−2)(z^2 −z−(1/2))=0 (c−1)(c+1)^3 (c^2 +c−(1/2))=0 cos t =±1∨cos t =−(1/2)±((√3)/2) ⇒ only solution is cos t =−(1/2)+((√3)/2) ⇒ sin^2 t =x=((√3)/2)

$$−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\wedge{x}\neq\mathrm{0} \\ $$$$\frac{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−\sqrt{\mathrm{1}+{x}}\right)}{{x}}+\frac{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}}\right)}{{x}}=\mathrm{1} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{3}/\mathrm{2}} +\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} =\mathrm{3}{x} \\ $$$$\mathrm{0}<{x}\leqslant\mathrm{1} \\ $$$${x}=\mathrm{sin}^{\mathrm{2}} \:{t} \\ $$$$\mathrm{cos}^{\mathrm{3}} \:{t}\:+\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{t}\right)^{\mathrm{3}/\mathrm{2}} =\mathrm{3sin}^{\mathrm{2}} \:{t} \\ $$$$\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{t}\right)^{\mathrm{3}} =\left(\mathrm{3sin}^{\mathrm{2}} \:{t}\:−\mathrm{cos}^{\mathrm{3}} \:{t}\right)^{\mathrm{2}} \\ $$$$\mathrm{sin}\:{t}\:={s}\wedge\mathrm{cos}\:{t}\:={c}\wedge{s}=\sqrt{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$${c}^{\mathrm{6}} +\mathrm{3}{c}^{\mathrm{5}} +\frac{\mathrm{3}}{\mathrm{2}}{c}^{\mathrm{4}} −\mathrm{3}{c}^{\mathrm{3}} −\mathrm{3}{c}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${c}={z}−\mathrm{1} \\ $$$${z}^{\mathrm{6}} −\mathrm{3}{z}^{\mathrm{5}} +\frac{\mathrm{3}}{\mathrm{2}}{z}^{\mathrm{4}} +{z}^{\mathrm{3}} =\mathrm{0} \\ $$$${z}^{\mathrm{3}} \left({z}−\mathrm{2}\right)\left({z}^{\mathrm{2}} −{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\left({c}−\mathrm{1}\right)\left({c}+\mathrm{1}\right)^{\mathrm{3}} \left({c}^{\mathrm{2}} +{c}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:{t}\:=\pm\mathrm{1}\vee\mathrm{cos}\:{t}\:=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{cos}\:{t}\:=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{sin}^{\mathrm{2}} \:{t}\:={x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 08/May/20

Thank you sir

$${Thank}\:{you}\:{sir} \\ $$

Commented by MJS last updated on 08/May/20

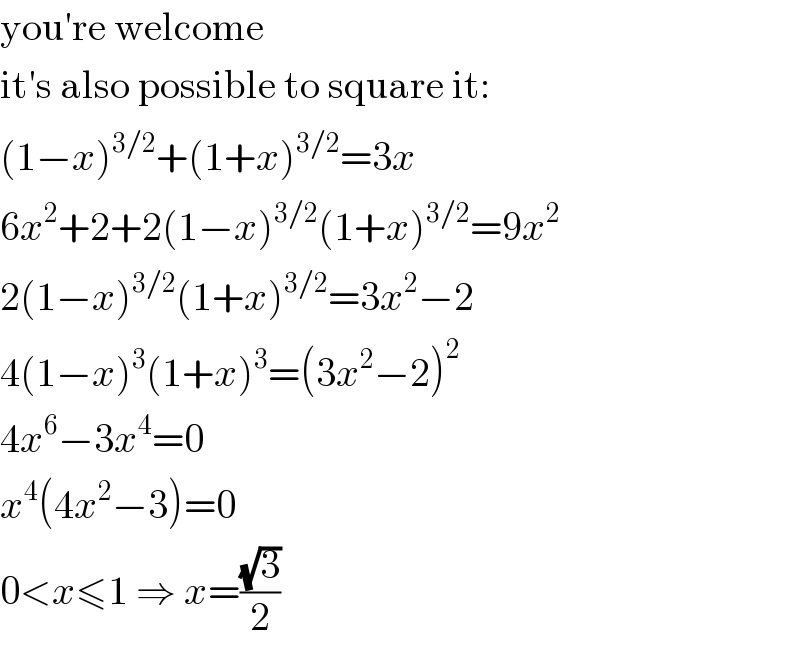
you′re welcome it′s also possible to square it: (1−x)^(3/2) +(1+x)^(3/2) =3x 6x^2 +2+2(1−x)^(3/2) (1+x)^(3/2) =9x^2 2(1−x)^(3/2) (1+x)^(3/2) =3x^2 −2 4(1−x)^3 (1+x)^3 =(3x^2 −2)^2 4x^6 −3x^4 =0 x^4 (4x^2 −3)=0 0<x≤1 ⇒ x=((√3)/2)

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{square}\:\mathrm{it}: \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{3}/\mathrm{2}} =\mathrm{3}{x} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{2}+\mathrm{2}\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{3}/\mathrm{2}} =\mathrm{9}{x}^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{3}/\mathrm{2}} =\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{4}\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \left(\mathrm{1}+{x}\right)^{\mathrm{3}} =\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{x}^{\mathrm{6}} −\mathrm{3}{x}^{\mathrm{4}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} \left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{0}<{x}\leqslant\mathrm{1}\:\Rightarrow\:{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 08/May/20

Nice sir thanks again

$${Nice}\:{sir}\:{thanks}\:{again} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com