Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 92717 by mr W last updated on 08/May/20

Commented by i jagooll last updated on 09/May/20

$(1) x^{3} + {9 x}^{2} y = 10$ $(2) {27 y}^{3} + {27 xy}^{2} = 54$ $(1) + (2)$ $x^{3} + {9 x}^{2} y + {27 xy}^{2} + {27 y}^{3} = 64$ ${(x + 3 y)}^{3} = 4^{3} \Rightarrow x + 3 y = 4$ $x = 4 - 3 y$ $\Rightarrow y^{3} + (4 - 3 y) y^{2} = 2$ $- {2 y}^{3} + {4 y}^{2} - 2 = 0$ $y^{3} - {2 y}^{2} + 1 = 0$ $(y - 1) (y^{2} - y - 1) = 0$ $y = 1 \Rightarrow x = 1$ $y = \frac{1 \pm \sqrt{5}}{2} \Rightarrow x = 4 - (\frac{3 \pm 3 \sqrt{5}}{2})$ $x = \frac{5 \mp 3 \sqrt{5}}{2}$
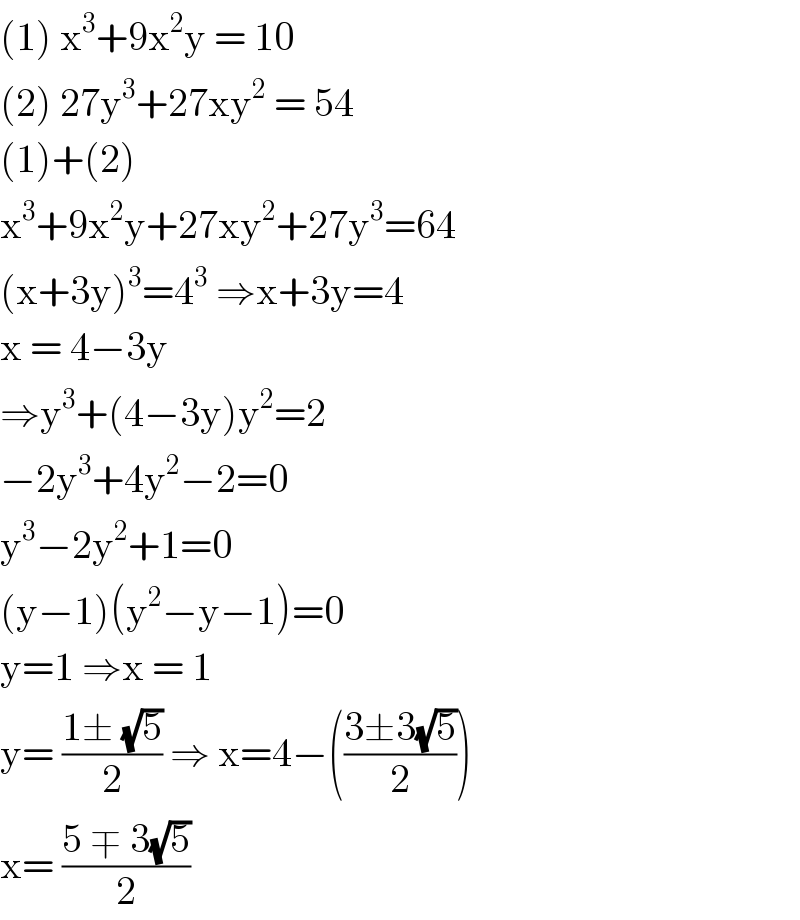
Commented by mr W last updated on 09/May/20

$r e s u l t n o t c o r r e c t s i r, i g o t :$ $x = 4 - 3 y$ $y^{3} + (4 - 3 y) y^{2} = 2$ $y^{3} - 2 y^{2} + 1 = 0$ $y^{3} - y^{2} - y^{2} + y - y + 1 = 0$ $(y - 1) y^{2} - (y - 1) y - (y - 1) = 0$ $(y - 1) (y^{2} - y - 1) = 0$ $y = 1 \Rightarrow x = 1$ $y = \frac{1 \pm \sqrt{5}}{2} \Rightarrow x = \frac{5 \mp 3 \sqrt{5}}{2}$
Commented by i jagooll last updated on 09/May/20

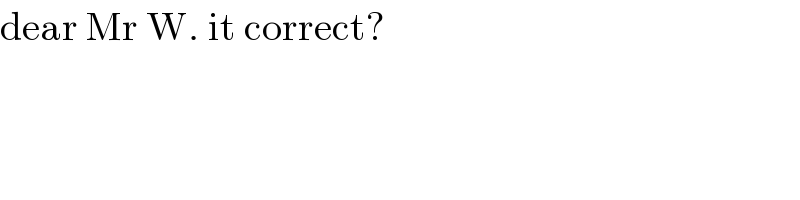
$dear Mr W . it correct ?$
Commented by i jagooll last updated on 09/May/20

$o yes sir . i typo$
Commented by john santu last updated on 09/May/20
greeatm..��
	Answered by Rasheed.Sindhi last updated on 08/May/20

	$x^{2} (x + 9 y) = 10$ $y^{2} (x + y) = 2$ $\frac{x^{2}}{y^{2}} \times (1 + \frac{8 y}{x + y}) = 5$ ${(\frac{x}{y})}^{2} (1 + \frac{1}{\frac{x + y}{8 y}}) = 5$ ${(\frac{x}{y})}^{2} (1 + \frac{1}{\frac{1}{8} (\frac{x}{y}) + \frac{1}{8}}) = 5$ $u^{2} (1 + \frac{1}{(1 / 8) (u + 1)}) = 5$ $u^{2} (\frac{(1 / 8) (u + 1) + 1}{(1 / 8) (u + 1)}) = 5$ $(1 / 8) u^{2} (u + 1) + u^{2} = (5 / 8) (u + 1)$ $u^{2} (u + 1) + 8 u^{2} = 5 (u + 1)$ $u^{3} + 9 u^{2} - 5 u - 5 = 0$ ${D o n}^{'} t k n o w t o s o l v e c u b i c e q u a t i o n .$ $. . . . . . . . .$ $. . . . .$
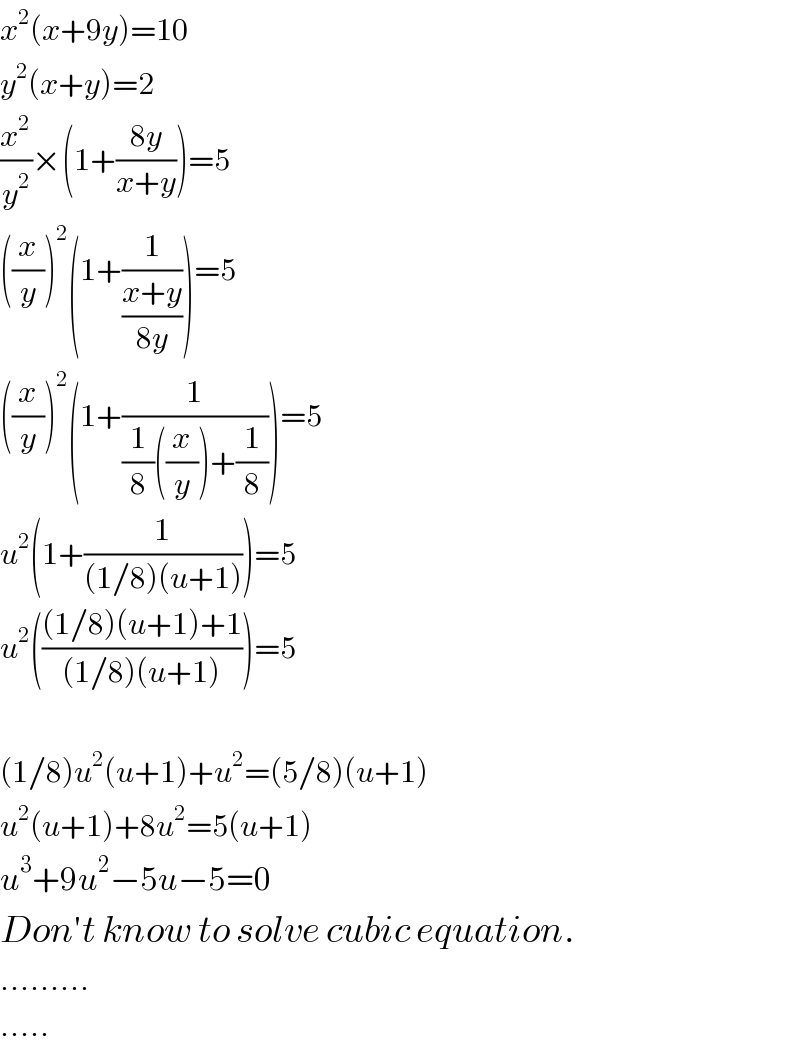
	Commented by Rio Michael last updated on 08/May/20

	$mind if i continue ?$ $u = 1 \Rightarrow {(1)}^{3} + 9 {(1)}^{2} - 5 (1) - (5) = 0$ $\Rightarrow if f (u) = u^{3} + 9 u^{2} - 5 u - 5$ $then u - 1 is a factor hence$ $f (u) = (u - 1) (u + 5 - \sqrt{20}) (u + 5 + \sqrt{20})$ $u = 1 or u = \sqrt{20} - 5 or u = - 5 - \sqrt{20}$
	Commented by mr W last updated on 08/May/20

	$t h a n k y o u b o t h!$
	Commented by Ar Brandon last updated on 09/May/20
	�� I love this spirit. Keep up Men.��
	Commented by Rasheed.Sindhi last updated on 13/May/20
	7ank5 5ir for encouraging!
	Answered by $@ty@m123 last updated on 10/May/20
	$((x^3 +9x^2 y)/(y^3 +xy^2 ))=5 ((((x/y))^3 +9((x/y))^2 )/(1+((x/y))))=5 t^3 +9t^2 −5t−5=0 {where t=(x/y) t^3 −t^2 +10t^2 −10t+5t−5=0 t^2 (t−1)+10t(t−1)+5(t−1)=0 (t−1)(t^2 +10t+5)=0 t=1, t=((−10±(√(100−20)))/2) t=1, t=−5±2(√5) Case 1. t=1 x=y=1. Case 2. t=−5+2(√5) ⇒x=(−5+2(√5))y ⇒y^3 +(−5+2(√5))y^3 =2 (−4+2(√5))y^3 =2 y^3 =(1/(−2+(√5))) y^3 =(1/((√5)−2))×(((√5)+2)/((√5)+2)) =(((√5)+2)/(5−4))=(√5)+2 y=((√5)+2)^(1/3) x=(−5+2(√5))((√5)+2)^(1/3) Case 3. t=−5−2(√5) ..... .....$
	$\frac{x^{3} + 9 x^{2} y}{y^{3} + {x y}^{2}} = 5$ $\frac{{(\frac{x}{y})}^{3} + 9 {(\frac{x}{y})}^{2}}{1 + (\frac{x}{y})} = 5$ $t^{3} + 9 t^{2} - 5 t - 5 = 0 {w h e r e t = \frac{x}{y}$ $t^{3} - t^{2} + 10 t^{2} - 10 t + 5 t - 5 = 0$ $t^{2} (t - 1) + 10 t (t - 1) + 5 (t - 1) = 0$ $(t - 1) (t^{2} + 10 t + 5) = 0$ $t = 1, t = \frac{- 10 \pm \sqrt{100 - 20}}{2}$ $t = 1, t = - 5 \pm 2 \sqrt{5}$ $C a s e 1 . t = 1$ $x = y = 1 .$ $C a s e 2 . t = - 5 + 2 \sqrt{5}$ $\Rightarrow x = (- 5 + 2 \sqrt{5}) y$ $\Rightarrow y^{3} + (- 5 + 2 \sqrt{5}) y^{3} = 2$ $(- 4 + 2 \sqrt{5}) y^{3} = 2$ $y^{3} = \frac{1}{- 2 + \sqrt{5}}$ $y^{3} = \frac{1}{\sqrt{5} - 2} \times \frac{\sqrt{5} + 2}{\sqrt{5} + 2}$ $= \frac{\sqrt{5} + 2}{5 - 4} = \sqrt{5} + 2$ $y = {(\sqrt{5} + 2)}^{\frac{1}{3}}$ $x = (- 5 + 2 \sqrt{5}) {(\sqrt{5} + 2)}^{\frac{1}{3}}$ $C a s e 3 . t = - 5 - 2 \sqrt{5}$ $. . . . .$ $. . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum