Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 9275 by geovane10math last updated on 27/Nov/16

About the Euler-Mascheroni Constant: γ = ∫_0 ^1 (1/(1 − x)) + (1/(ln x)) dx We can see that 1− x ≠ 0 ⇔ 1 ≠ x ; x = 0 → ln x ∄ . If x ≠ 0 and x ≠ 1, in the Cartesian Plane, this function has singularity x=0 and x=1. So, I could write f(x) = (1/(1 − x)) + (1/(ln x)) ∫_0 ^1 f(x) dx = lim_(A→0^+ ) lim_(B→1^− ) ∫_A ^B f(x) dx ? PS: Sorry by my worse English

$$\mathrm{About}\:\mathrm{the}\:\mathrm{Euler}-\mathrm{Mascheroni}\:\mathrm{Constant}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\gamma\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}\:−\:{x}}\:+\:\frac{\mathrm{1}}{\mathrm{ln}\:{x}}\:{dx} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that}\: \\ $$$$\:\mathrm{1}−\:{x}\:\neq\:\mathrm{0}\:\Leftrightarrow\:\mathrm{1}\:\neq\:{x}\:; \\ $$$${x}\:=\:\mathrm{0}\:\rightarrow\:\mathrm{ln}\:{x}\:\nexists\:. \\ $$$$\mathrm{If}\:{x}\:\neq\:\mathrm{0}\:\mathrm{and}\:{x}\:\neq\:\mathrm{1},\:\mathrm{in}\:\mathrm{the}\:\mathrm{Cartesian}\:\mathrm{Plane}, \\ $$$$\mathrm{this}\:\mathrm{function}\:\mathrm{has}\:\mathrm{singularity}\:{x}=\mathrm{0}\:{and}\:{x}=\mathrm{1}. \\ $$$$\mathrm{So},\:\mathrm{I}\:\mathrm{could}\:\mathrm{write} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}\:−\:{x}}\:+\:\frac{\mathrm{1}}{\mathrm{ln}\:{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right)\:{dx}\:=\:\underset{{A}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\underset{{B}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\int_{{A}} ^{{B}} {f}\left({x}\right)\:{dx}\:\:? \\ $$$${PS}:\:{Sorry}\:{by}\:{my}\:{worse}\:{English} \\ $$

Commented by geovane10math last updated on 27/Nov/16

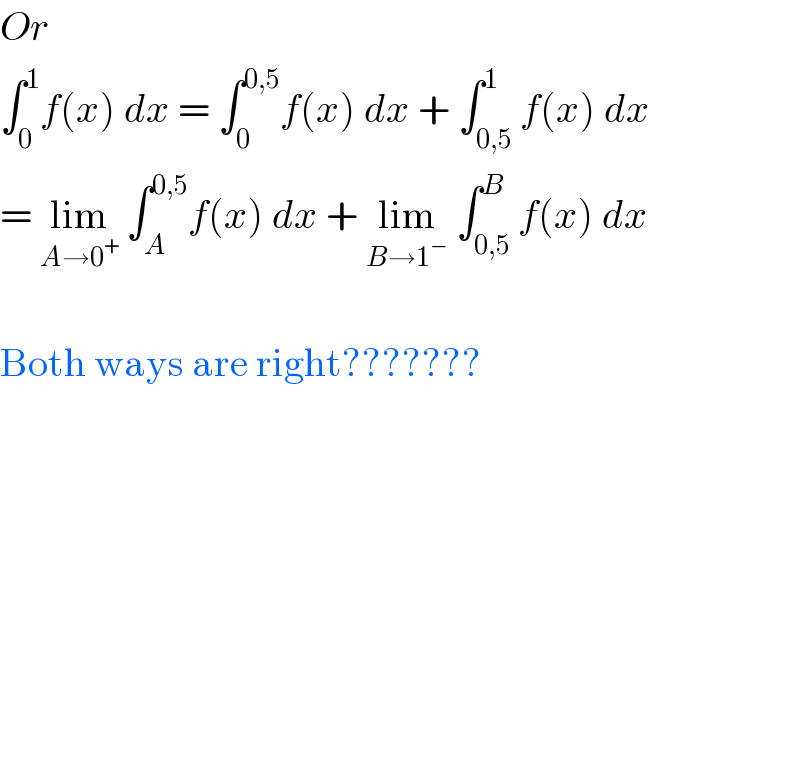
Or ∫_0 ^1 f(x) dx = ∫_0 ^(0,5) f(x) dx + ∫_(0,5) ^1 f(x) dx = lim_(A→0^+ ) ∫_A ^(0,5) f(x) dx + lim_(B→1^− ) ∫_(0,5) ^B f(x) dx Both ways are right???????

$${Or}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right)\:{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{0},\mathrm{5}} {f}\left({x}\right)\:{dx}\:+\:\int_{\mathrm{0},\mathrm{5}} ^{\mathrm{1}} {f}\left({x}\right)\:{dx} \\ $$$$=\:\underset{{A}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\int_{{A}} ^{\mathrm{0},\mathrm{5}} {f}\left({x}\right)\:{dx}\:+\:\underset{{B}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\int_{\mathrm{0},\mathrm{5}} ^{{B}} {f}\left({x}\right)\:{dx} \\ $$$$ \\ $$$$\mathrm{Both}\:\mathrm{ways}\:\mathrm{are}\:\mathrm{right}??????? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by 123456 last updated on 28/Nov/16

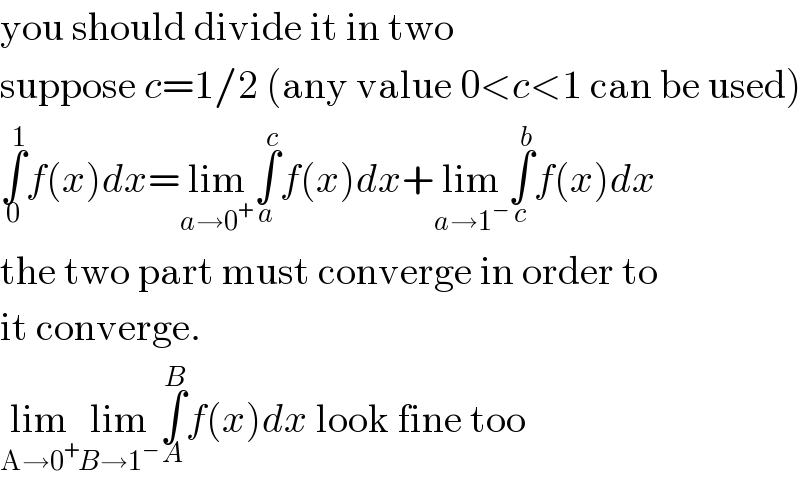
you should divide it in two suppose c=1/2 (any value 0<c<1 can be used) ∫_0 ^1 f(x)dx=lim_(a→0^+ ) ∫_a ^c f(x)dx+lim_(a→1^− ) ∫_c ^b f(x)dx the two part must converge in order to it converge. lim_(A→0^+ ) lim_(B→1^− ) ∫_A ^B f(x)dx look fine too

$$\mathrm{you}\:\mathrm{should}\:\mathrm{divide}\:\mathrm{it}\:\mathrm{in}\:\mathrm{two} \\ $$$$\mathrm{suppose}\:{c}=\mathrm{1}/\mathrm{2}\:\left(\mathrm{any}\:\mathrm{value}\:\mathrm{0}<{c}<\mathrm{1}\:\mathrm{can}\:\mathrm{be}\:\mathrm{used}\right) \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}=\underset{{a}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\underset{{a}} {\overset{{c}} {\int}}{f}\left({x}\right){dx}+\underset{{a}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\underset{{c}} {\overset{{b}} {\int}}{f}\left({x}\right){dx} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{part}\:\mathrm{must}\:\mathrm{converge}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to} \\ $$$$\mathrm{it}\:\mathrm{converge}. \\ $$$$\underset{\mathrm{A}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\underset{{B}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\underset{{A}} {\overset{{B}} {\int}}{f}\left({x}\right){dx}\:\mathrm{look}\:\mathrm{fine}\:\mathrm{too} \\ $$

Commented by geovane10math last updated on 28/Nov/16

Thanks!

$${Thanks}! \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com