Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 92804 by niroj last updated on 09/May/20

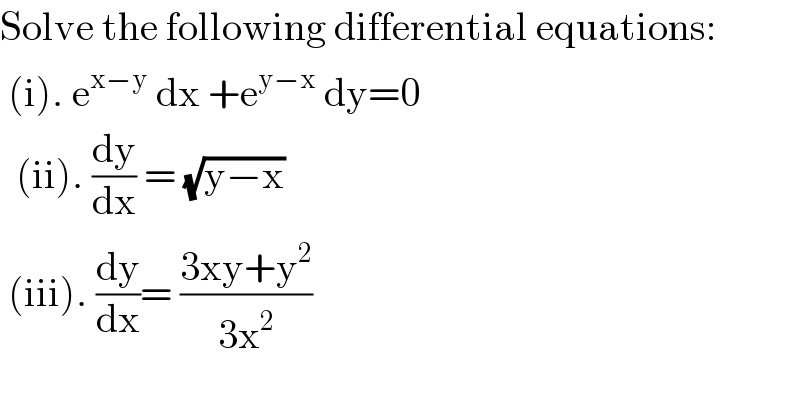
Solve the following differential equations: (i). e^(x−y) dx +e^(y−x) dy=0 (ii). (dy/dx) = (√(y−x)) (iii). (dy/dx)= ((3xy+y^2 )/(3x^2 ))

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{following}\:\mathrm{differential}\:\mathrm{equations}: \\ $$$$\:\left(\mathrm{i}\right).\:\mathrm{e}^{\mathrm{x}−\mathrm{y}} \:\mathrm{dx}\:+\mathrm{e}^{\mathrm{y}−\mathrm{x}} \:\mathrm{dy}=\mathrm{0} \\ $$$$\:\:\left(\mathrm{ii}\right).\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\sqrt{\mathrm{y}−\mathrm{x}} \\ $$$$\:\left(\mathrm{iii}\right).\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\frac{\mathrm{3xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{3x}^{\mathrm{2}} } \\ $$$$ \\ $$

Commented by john santu last updated on 09/May/20

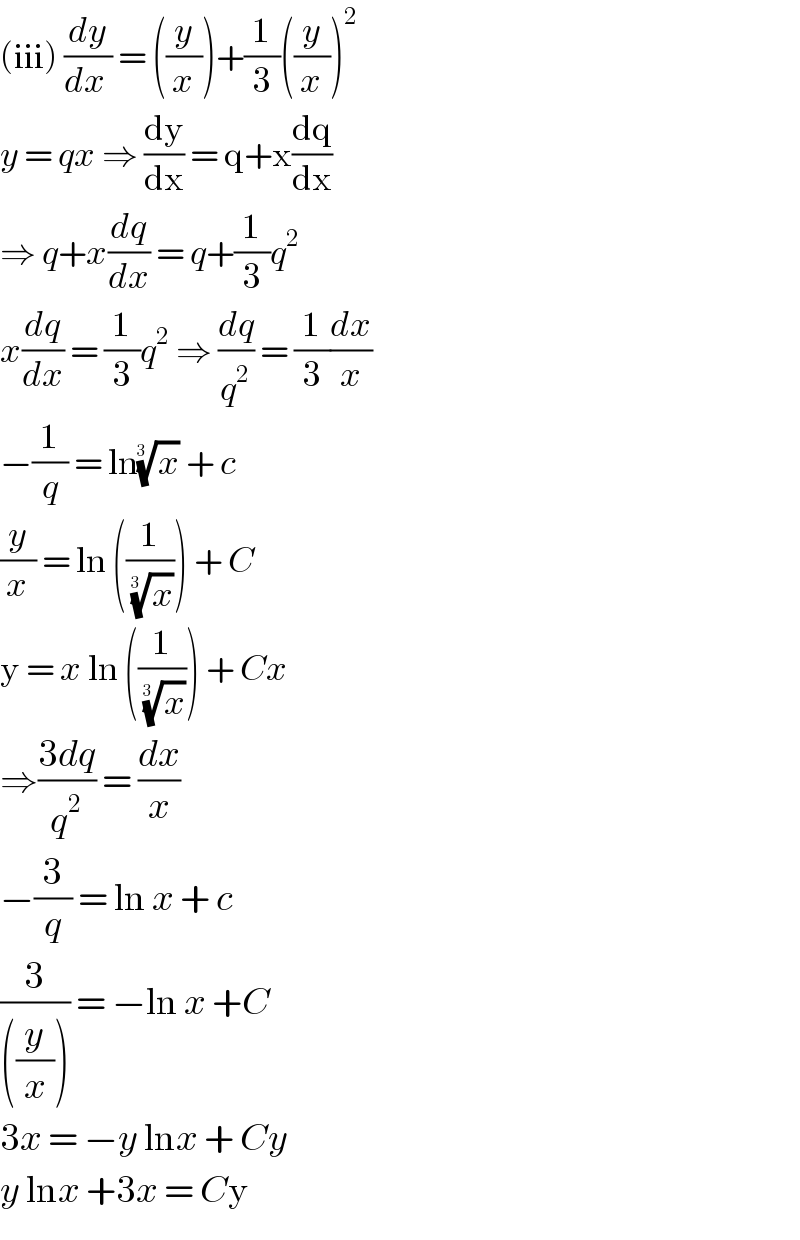
(iii) (dy/(dx )) = ((y/x))+(1/3)((y/x))^2 y = qx ⇒ (dy/dx) = q+x(dq/dx) ⇒ q+x(dq/dx) = q+(1/3)q^2 x(dq/dx) = (1/3)q^2 ⇒ (dq/q^2 ) = (1/3)(dx/x) −(1/q) = ln(x)^(1/(3 )) + c (y/x) = ln ((1/(x)^(1/(3 )) )) + C y = x ln ((1/(x)^(1/(3 )) )) + Cx ⇒((3dq)/q^2 ) = (dx/x) −(3/q) = ln x + c (3/(((y/x)))) = −ln x +C 3x = −y lnx + Cy y lnx +3x = Cy

$$\left(\mathrm{iii}\right)\:\frac{{dy}}{{dx}\:}\:=\:\left(\frac{{y}}{{x}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \\ $$$${y}\:=\:{qx}\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{q}+\mathrm{x}\frac{\mathrm{dq}}{\mathrm{dx}} \\ $$$$\Rightarrow\:{q}+{x}\frac{{dq}}{{dx}}\:=\:{q}+\frac{\mathrm{1}}{\mathrm{3}}{q}^{\mathrm{2}} \\ $$$${x}\frac{{dq}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{q}^{\mathrm{2}} \:\Rightarrow\:\frac{{dq}}{{q}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}\frac{{dx}}{{x}} \\ $$$$−\frac{\mathrm{1}}{{q}}\:=\:\mathrm{ln}\sqrt[{\mathrm{3}\:\:}]{{x}}\:+\:{c}\: \\ $$$$\frac{{y}}{{x}}\:=\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{\sqrt[{\mathrm{3}\:\:}]{{x}}}\right)\:+\:{C} \\ $$$$\mathrm{y}\:=\:{x}\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{\sqrt[{\mathrm{3}\:\:}]{{x}}}\right)\:+\:{Cx} \\ $$$$\Rightarrow\frac{\mathrm{3}{dq}}{{q}^{\mathrm{2}} }\:=\:\frac{{dx}}{{x}} \\ $$$$−\frac{\mathrm{3}}{{q}}\:=\:\mathrm{ln}\:{x}\:+\:{c}\: \\ $$$$\frac{\mathrm{3}}{\left(\frac{{y}}{{x}}\right)}\:=\:−\mathrm{ln}\:{x}\:+{C} \\ $$$$\mathrm{3}{x}\:=\:−{y}\:\mathrm{ln}{x}\:+\:{Cy}\: \\ $$$${y}\:\mathrm{ln}{x}\:+\mathrm{3}{x}\:=\:{C}\mathrm{y} \\ $$

Commented by niroj last updated on 09/May/20

I really thanks full your efforts mr.john santu�� it may be result should better: 3x + y log x = cy .��

Commented by john santu last updated on 09/May/20

how your got it?

$$\mathrm{how}\:\mathrm{your}\:\mathrm{got}\:\mathrm{it}? \\ $$

Commented by mr W last updated on 09/May/20

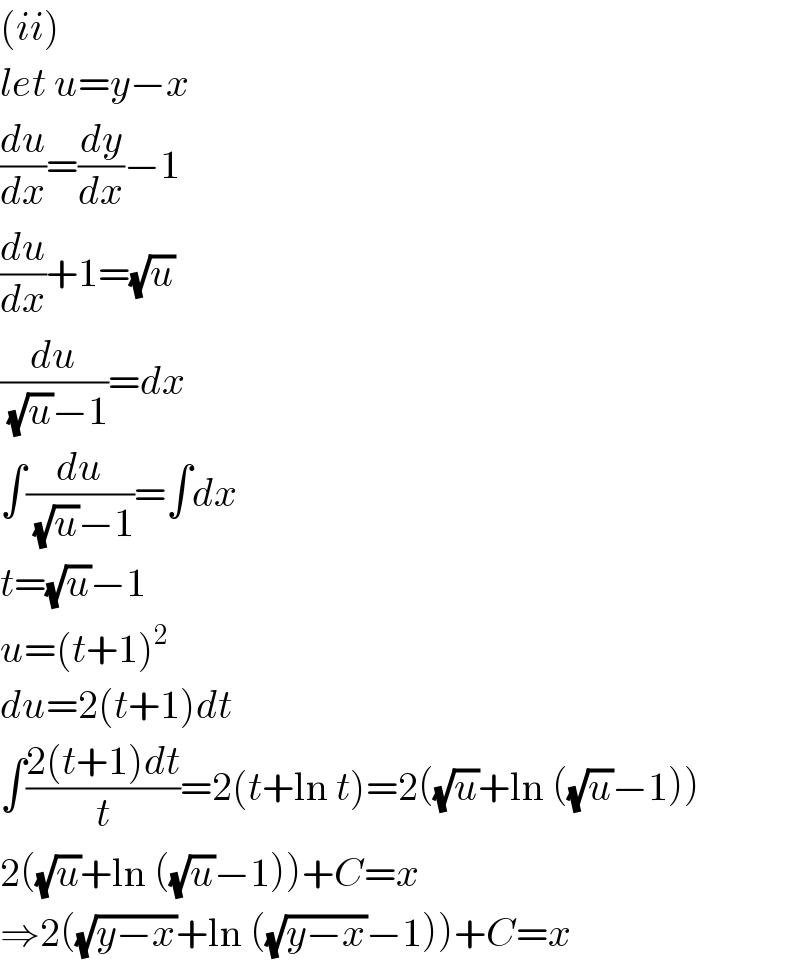
(ii) let u=y−x (du/dx)=(dy/dx)−1 (du/dx)+1=(√u) (du/((√u)−1))=dx ∫(du/((√u)−1))=∫dx t=(√u)−1 u=(t+1)^2 du=2(t+1)dt ∫((2(t+1)dt)/t)=2(t+ln t)=2((√u)+ln ((√u)−1)) 2((√u)+ln ((√u)−1))+C=x ⇒2((√(y−x))+ln ((√(y−x))−1))+C=x

$$\left({ii}\right) \\ $$$${let}\:{u}={y}−{x} \\ $$$$\frac{{du}}{{dx}}=\frac{{dy}}{{dx}}−\mathrm{1} \\ $$$$\frac{{du}}{{dx}}+\mathrm{1}=\sqrt{{u}} \\ $$$$\frac{{du}}{\sqrt{{u}}−\mathrm{1}}={dx} \\ $$$$\int\frac{{du}}{\sqrt{{u}}−\mathrm{1}}=\int{dx} \\ $$$${t}=\sqrt{{u}}−\mathrm{1} \\ $$$${u}=\left({t}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${du}=\mathrm{2}\left({t}+\mathrm{1}\right){dt} \\ $$$$\int\frac{\mathrm{2}\left({t}+\mathrm{1}\right){dt}}{{t}}=\mathrm{2}\left({t}+\mathrm{ln}\:{t}\right)=\mathrm{2}\left(\sqrt{{u}}+\mathrm{ln}\:\left(\sqrt{{u}}−\mathrm{1}\right)\right) \\ $$$$\mathrm{2}\left(\sqrt{{u}}+\mathrm{ln}\:\left(\sqrt{{u}}−\mathrm{1}\right)\right)+{C}={x} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{{y}−{x}}+\mathrm{ln}\:\left(\sqrt{{y}−{x}}−\mathrm{1}\right)\right)+{C}={x} \\ $$

Commented by niroj last updated on 09/May/20

Nice solution dear����

Commented by john santu last updated on 09/May/20

differential equation is exactly the same as integral, the answer can be more than 1 form

Commented by john santu last updated on 09/May/20

and no measure states that one form is better than another. because there must be differences in viewpoints. hair can be the same black but the contents of the head are different. ha ha ha..

Commented by niroj last updated on 09/May/20

I agree your openion my dear.

$$\:\mathrm{I}\:\mathrm{agree}\:\mathrm{your}\:\mathrm{openion}\:\mathrm{my}\:\mathrm{dear}. \\ $$

Commented by john santu last updated on 09/May/20

cooll man ����

Commented by john santu last updated on 09/May/20

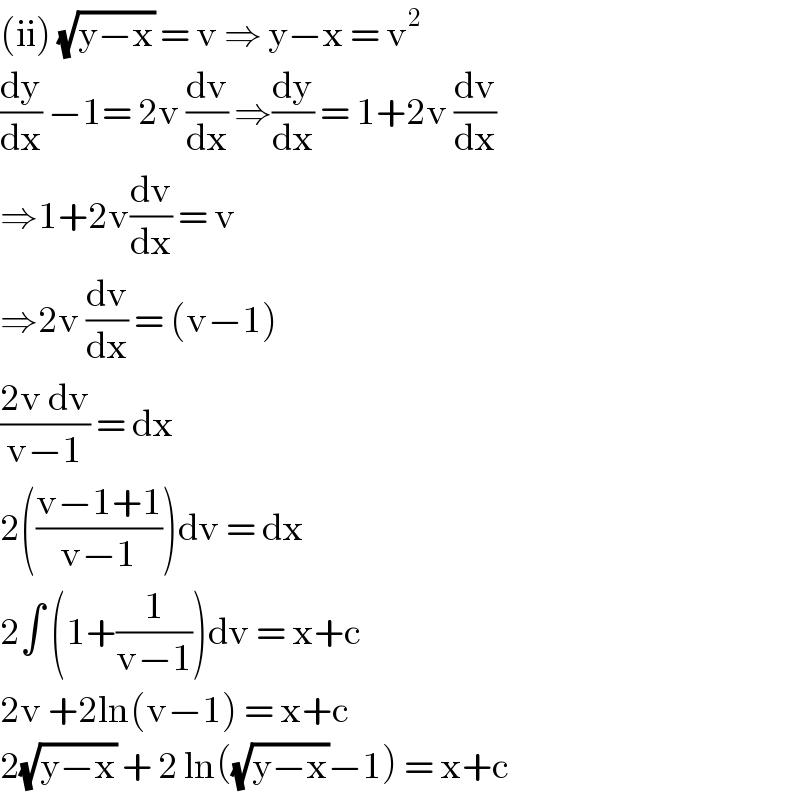
(ii) (√(y−x)) = v ⇒ y−x = v^2 (dy/dx) −1= 2v (dv/dx) ⇒(dy/dx) = 1+2v (dv/dx) ⇒1+2v(dv/dx) = v ⇒2v (dv/dx) = (v−1) ((2v dv)/(v−1)) = dx 2(((v−1+1)/(v−1)))dv = dx 2∫ (1+(1/(v−1)))dv = x+c 2v +2ln(v−1) = x+c 2(√(y−x)) + 2 ln((√(y−x))−1) = x+c

$$\left(\mathrm{ii}\right)\:\sqrt{\mathrm{y}−\mathrm{x}}\:=\:\mathrm{v}\:\Rightarrow\:\mathrm{y}−\mathrm{x}\:=\:\mathrm{v}^{\mathrm{2}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:−\mathrm{1}=\:\mathrm{2v}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{1}+\mathrm{2v}\:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2v}\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{v}\: \\ $$$$\Rightarrow\mathrm{2v}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\left(\mathrm{v}−\mathrm{1}\right)\: \\ $$$$\frac{\mathrm{2v}\:\mathrm{dv}}{\mathrm{v}−\mathrm{1}}\:=\:\mathrm{dx}\: \\ $$$$\mathrm{2}\left(\frac{\mathrm{v}−\mathrm{1}+\mathrm{1}}{\mathrm{v}−\mathrm{1}}\right)\mathrm{dv}\:=\:\mathrm{dx}\: \\ $$$$\mathrm{2}\int\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{v}−\mathrm{1}}\right)\mathrm{dv}\:=\:\mathrm{x}+\mathrm{c} \\ $$$$\mathrm{2v}\:+\mathrm{2ln}\left(\mathrm{v}−\mathrm{1}\right)\:=\:\mathrm{x}+\mathrm{c}\: \\ $$$$\mathrm{2}\sqrt{\mathrm{y}−\mathrm{x}}\:+\:\mathrm{2}\:\mathrm{ln}\left(\sqrt{\mathrm{y}−\mathrm{x}}−\mathrm{1}\right)\:=\:\mathrm{x}+\mathrm{c} \\ $$

Commented by niroj last updated on 09/May/20

Now mission is complete Mr.John Santu while I aspect thank for your pleasure time����������

Commented by peter frank last updated on 09/May/20

thank you both

$${thank}\:{you}\:{both} \\ $$

Answered by mr W last updated on 09/May/20

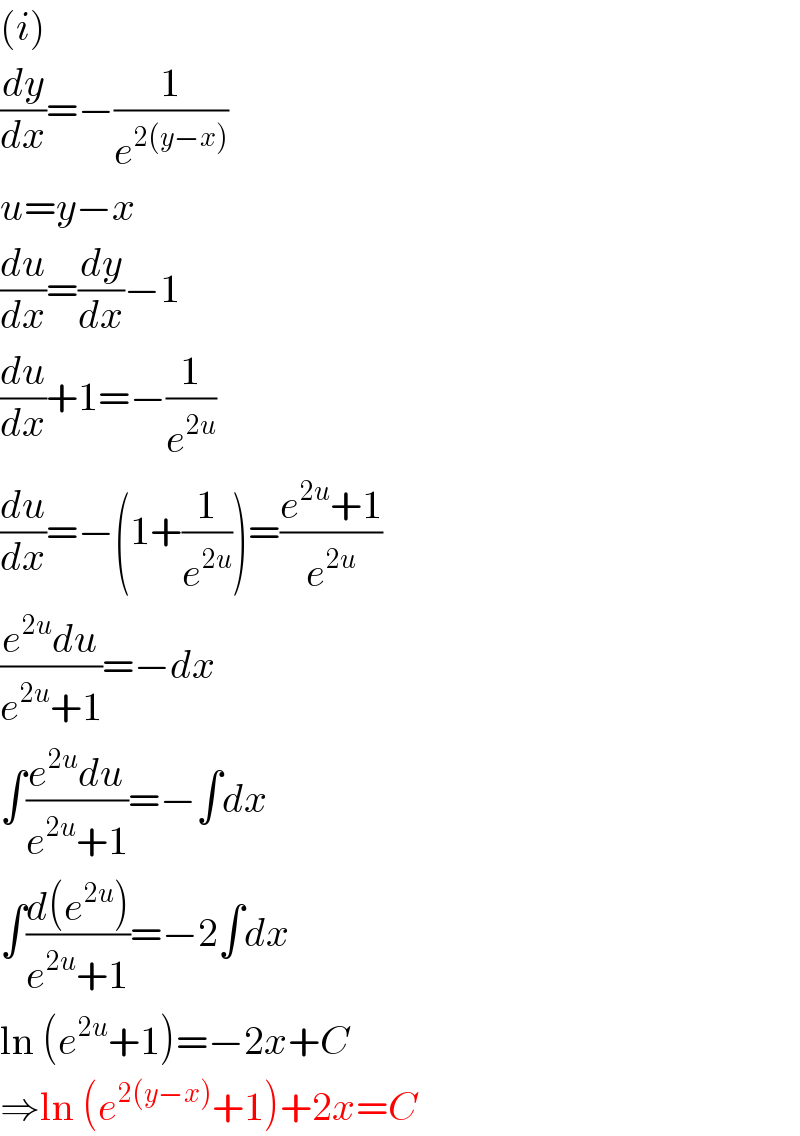
(i) (dy/dx)=−(1/e^(2(y−x)) ) u=y−x (du/dx)=(dy/dx)−1 (du/dx)+1=−(1/e^(2u) ) (du/dx)=−(1+(1/e^(2u) ))=((e^(2u) +1)/e^(2u) ) ((e^(2u) du)/(e^(2u) +1))=−dx ∫((e^(2u) du)/(e^(2u) +1))=−∫dx ∫((d(e^(2u) ))/(e^(2u) +1))=−2∫dx ln (e^(2u) +1)=−2x+C ⇒ln (e^(2(y−x)) +1)+2x=C

$$\left({i}\right) \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{e}^{\mathrm{2}\left({y}−{x}\right)} } \\ $$$${u}={y}−{x} \\ $$$$\frac{{du}}{{dx}}=\frac{{dy}}{{dx}}−\mathrm{1} \\ $$$$\frac{{du}}{{dx}}+\mathrm{1}=−\frac{\mathrm{1}}{{e}^{\mathrm{2}{u}} } \\ $$$$\frac{{du}}{{dx}}=−\left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{\mathrm{2}{u}} }\right)=\frac{{e}^{\mathrm{2}{u}} +\mathrm{1}}{{e}^{\mathrm{2}{u}} } \\ $$$$\frac{{e}^{\mathrm{2}{u}} {du}}{{e}^{\mathrm{2}{u}} +\mathrm{1}}=−{dx} \\ $$$$\int\frac{{e}^{\mathrm{2}{u}} {du}}{{e}^{\mathrm{2}{u}} +\mathrm{1}}=−\int{dx} \\ $$$$\int\frac{{d}\left({e}^{\mathrm{2}{u}} \right)}{{e}^{\mathrm{2}{u}} +\mathrm{1}}=−\mathrm{2}\int{dx} \\ $$$$\mathrm{ln}\:\left({e}^{\mathrm{2}{u}} +\mathrm{1}\right)=−\mathrm{2}{x}+{C} \\ $$$$\Rightarrow\mathrm{ln}\:\left({e}^{\mathrm{2}\left({y}−{x}\right)} +\mathrm{1}\right)+\mathrm{2}{x}={C} \\ $$

Commented by john santu last updated on 09/May/20

great prof

$$\mathrm{great}\:\mathrm{prof}\: \\ $$

Commented by niroj last updated on 09/May/20

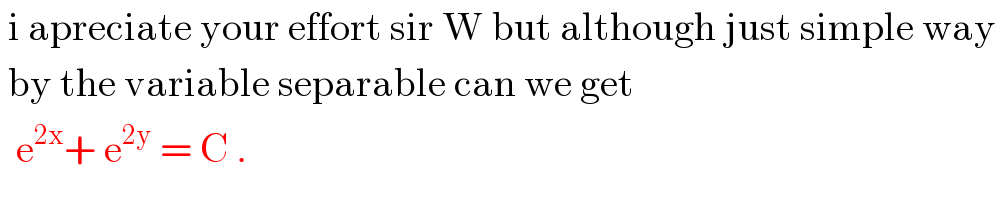
i apreciate your effort sir W but although just simple way by the variable separable can we get e^(2x) + e^(2y) = C .

$$\:\mathrm{i}\:\mathrm{apreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}\:\mathrm{W}\:\mathrm{but}\:\mathrm{although}\:\mathrm{just}\:\mathrm{simple}\:\mathrm{way} \\ $$$$\:\mathrm{by}\:\mathrm{the}\:\mathrm{variable}\:\mathrm{separable}\:\mathrm{can}\:\mathrm{we}\:\mathrm{get}\:\: \\ $$$$\:\:\mathrm{e}^{\mathrm{2x}} +\:\mathrm{e}^{\mathrm{2y}} \:=\:\mathrm{C}\:. \\ $$

Commented by otchereabdullai@gmail.com last updated on 09/May/20

sir John thanks for respecting his tittle of honoury prof W

$$\mathrm{sir}\:\mathrm{John}\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{respecting}\:\mathrm{his}\:\mathrm{tittle} \\ $$$$\mathrm{of}\:\mathrm{honoury}\:\mathrm{prof}\:\mathrm{W} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com