Evaluate: ∫_R ∫ ((xy)/(√(1−y^2 ))) dx dy where the region of integration is the positive quadrant of the circle x^2 +y^2 =1.


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 92805 by niroj last updated on 09/May/20

$Evaluate :$ $\int_{R} \int \frac{xy}{\sqrt{1 - y^{2}}} dx dy where the region of integration is the$ $positive quadrant of the circle x^{2} + y^{2} = 1 .$
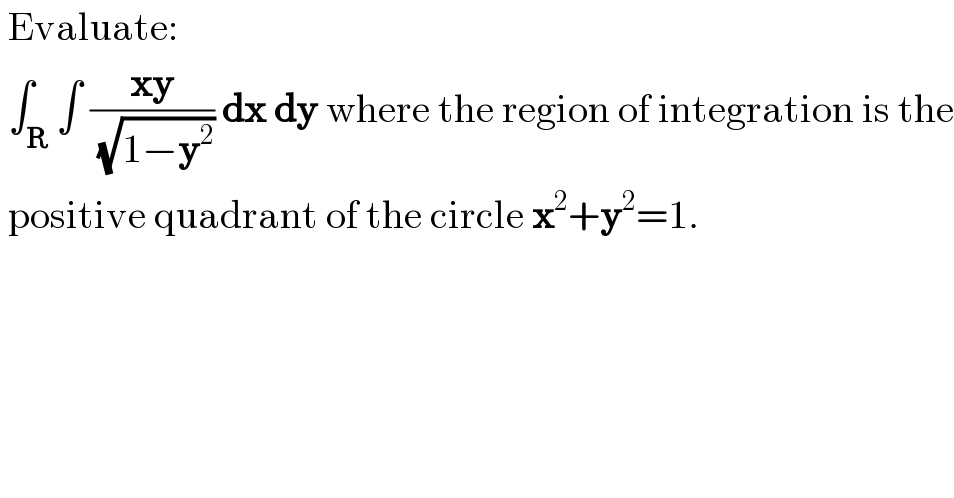
	Answered by mr W last updated on 09/May/20
	$=∫_0 ^(π/2) ∫_0 ^1 ((r^2 cos θ sin θ)/(√(1−r^2 sin^2 θ)))rdrdθ =(1/2)∫_0 ^(π/2) cos θ sin θ(∫_0 ^1 (r^2 /(√(1−r^2 sin^2 θ)))dr^2 )dθ =(1/2)∫_0 ^(π/2) cos θ sin θ(∫_0 ^1 (u/(√(1−u sin^2 θ)))du)dθ =(1/2)∫_0 ^(π/2) cos θ sin θ(1/(sin^2 θ)){∫_0 ^1 [−(√(1−u sin^2 θ))+(1/(√(1−u sin^2 θ)))]du}dθ =(1/2)∫_0 ^(π/2) ((cos θ)/(sin θ)){[(2/(3 sin^2 θ))(1−u sin^2 θ)^(3/2) −(2/(sin^2 θ))(√(1−u sin^2 θ))]_0 ^1 }dθ =(1/2)∫_0 ^(π/2) ((cos θ)/(sin θ)){[(2/(3 sin^2 θ))(1−sin^2 θ)^(3/2) −(2/(3 sin^2 θ))−(2/(sin^2 θ))(√(1−sin^2 θ))+(2/(sin^2 θ))]}dθ =(1/3)∫_0 ^(π/2) ((cos θ)/(sin θ))[((cos^3 θ−3cos θ+2)/(sin^2 θ))]dθ =(1/3)∫_(π/2) ^0 (((cos^3 θ−3cos θ+2)cos θ)/((1−cos^2 θ)^2 ))d(cos θ) =(1/3)∫_0 ^1 (((t^3 −3t+2)t)/((1−t^2 )^2 ))dt =(1/3)∫_0 ^1 (((t+2)t)/((t+1)^2 ))dt =(1/3)∫_0 ^1 [1−(1/((t+1)^2 ))]dt =(1/3)[t+(1/(t+1))]_0 ^1 =(1/3)(1+(1/2)−1) =(1/6)$
	$= \int_{0}^{\frac{π}{2}} \int_{0}^{1} \frac{r^{2} \cos θ \sin θ}{\sqrt{1 - r^{2} \sin^{2} θ}} r d r d θ$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \cos θ \sin θ (\int_{0}^{1} \frac{r^{2}}{\sqrt{1 - r^{2} \sin^{2} θ}} {d r}^{2}) d θ$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \cos θ \sin θ (\int_{0}^{1} \frac{u}{\sqrt{1 - u \sin^{2} θ}} d u) d θ$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \cos θ \sin θ \frac{1}{\sin^{2} θ} {\int_{0}^{1} [- \sqrt{1 - u \sin^{2} θ} + \frac{1}{\sqrt{1 - u \sin^{2} θ}}] d u} d θ$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{\cos θ}{\sin θ} {{[\frac{2}{3 \sin^{2} θ} {(1 - u \sin^{2} θ)}^{\frac{3}{2}} - \frac{2}{\sin^{2} θ} \sqrt{1 - u \sin^{2} θ}]}_{0}^{1}} d θ$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{\cos θ}{\sin θ} {[\frac{2}{3 \sin^{2} θ} {(1 - \sin^{2} θ)}^{\frac{3}{2}} - \frac{2}{3 \sin^{2} θ} - \frac{2}{\sin^{2} θ} \sqrt{1 - \sin^{2} θ} + \frac{2}{\sin^{2} θ}]} d θ$ $= \frac{1}{3} \int_{0}^{\frac{π}{2}} \frac{\cos θ}{\sin θ} [\frac{\cos^{3} θ - 3 \cos θ + 2}{\sin^{2} θ}] d θ$ $= \frac{1}{3} \int_{\frac{π}{2}}^{0} \frac{(\cos^{3} θ - 3 \cos θ + 2) \cos θ}{{(1 - \cos^{2} θ)}^{2}} d (\cos θ)$ $= \frac{1}{3} \int_{0}^{1} \frac{(t^{3} - 3 t + 2) t}{{(1 - t^{2})}^{2}} d t$ $= \frac{1}{3} \int_{0}^{1} \frac{(t + 2) t}{{(t + 1)}^{2}} d t$ $= \frac{1}{3} \int_{0}^{1} [1 - \frac{1}{{(t + 1)}^{2}}] d t$ $= \frac{1}{3} {[t + \frac{1}{t + 1}]}_{0}^{1}$ $= \frac{1}{3} (1 + \frac{1}{2} - 1)$ $= \frac{1}{6}$
	Commented by niroj last updated on 09/May/20
	Thank you Mr. W It is aspected result ��
	Commented by Ar Brandon last updated on 09/May/20
	��
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum