Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 92852 by i jagooll last updated on 09/May/20

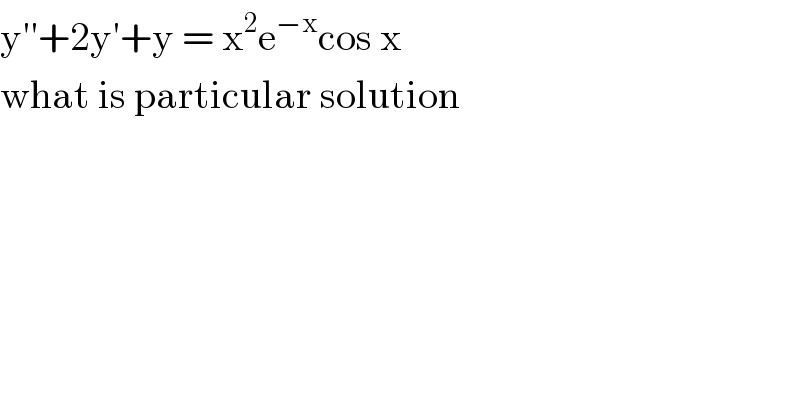
y′′+2y′+y = x^2 e^(−x) cos x what is particular solution

$$\mathrm{y}''+\mathrm{2y}'+\mathrm{y}\:=\:\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{particular}\:\mathrm{solution} \\ $$$$ \\ $$

Commented by i jagooll last updated on 09/May/20

Mr Niroj's favorite ����

Answered by Joel578 last updated on 09/May/20

• Homogeneous solution with char. eq. λ^2 + 2λ + 1 = 0 → λ_(1,2) = −1 ⇒ y_h (x) = c_1 e^(−x) + c_2 xe^(−x) • Particular solution for r(x) = x^2 e^(−x) cos x using variation of parameters Let y_p (x) = u(x)y_1 (x) + v(x)y_2 (x) with y_1 (x) = e^(−x) , y_2 (x) = xe^(−x) and u(x) = −∫ ((r(x)y_2 (x))/(W(x))) dx, v(x) = ∫ ((r(x)y_1 (x))/(W(x))) dx Now, W(x) = determinant ((y_1 ,y_2 ),((y_1 ′),(y_2 ′)))= determinant ((( e^(−x) ),( xe^(−x) )),((−e^(−x) ),(e^(−x) − xe^(−x) ))) = e^(−2x) Hence, u(x) = −∫ (((x^2 e^(−x) cos x)(xe^(−x) ))/e^(−2x) ) dx = −∫ x^3 cos x dx v(x) = ∫ (((x^2 e^(−x) cos x)(e^(−x) ))/e^(−2x) ) dx = ∫ x^2 cos x dx ⇒ y_p (x) = ...

$$\bullet\:\mathrm{Homogeneous}\:\mathrm{solution}\:\mathrm{with}\:\mathrm{char}.\:\mathrm{eq}. \\ $$$$\lambda^{\mathrm{2}} \:+\:\mathrm{2}\lambda\:+\:\mathrm{1}\:=\:\mathrm{0}\:\rightarrow\:\lambda_{\mathrm{1},\mathrm{2}} \:=\:−\mathrm{1} \\ $$$$\Rightarrow\:{y}_{{h}} \left({x}\right)\:=\:{c}_{\mathrm{1}} {e}^{−{x}} \:+\:{c}_{\mathrm{2}} {xe}^{−{x}} \\ $$$$ \\ $$$$\bullet\:\mathrm{Particular}\:\mathrm{solution}\:\mathrm{for}\:{r}\left({x}\right)\:=\:{x}^{\mathrm{2}} {e}^{−{x}} \mathrm{cos}\:{x} \\ $$$$\mathrm{using}\:\mathrm{variation}\:\mathrm{of}\:\mathrm{parameters} \\ $$$$\mathrm{Let}\:{y}_{{p}} \left({x}\right)\:=\:{u}\left({x}\right){y}_{\mathrm{1}} \left({x}\right)\:+\:{v}\left({x}\right){y}_{\mathrm{2}} \left({x}\right) \\ $$$$\mathrm{with}\:{y}_{\mathrm{1}} \left({x}\right)\:=\:{e}^{−{x}} ,\:\:\:{y}_{\mathrm{2}} \left({x}\right)\:=\:{xe}^{−{x}} \\ $$$$\mathrm{and}\:{u}\left({x}\right)\:=\:−\int\:\frac{{r}\left({x}\right){y}_{\mathrm{2}} \left({x}\right)}{{W}\left({x}\right)}\:{dx},\:\:{v}\left({x}\right)\:=\:\int\:\frac{{r}\left({x}\right){y}_{\mathrm{1}} \left({x}\right)}{{W}\left({x}\right)}\:{dx} \\ $$$$\mathrm{Now},\: \\ $$$${W}\left({x}\right)\:=\:\begin{vmatrix}{{y}_{\mathrm{1}} }&{{y}_{\mathrm{2}} }\\{{y}_{\mathrm{1}} '}&{{y}_{\mathrm{2}} '}\end{vmatrix}=\:\begin{vmatrix}{\:\:{e}^{−{x}} }&{\:\:\:\:\:\:\:{xe}^{−{x}} }\\{−{e}^{−{x}} }&{{e}^{−{x}} \:−\:{xe}^{−{x}} }\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{e}^{−\mathrm{2}{x}} \\ $$$$\mathrm{Hence}, \\ $$$${u}\left({x}\right)\:=\:−\int\:\frac{\left({x}^{\mathrm{2}} {e}^{−{x}} \mathrm{cos}\:{x}\right)\left({xe}^{−{x}} \right)}{{e}^{−\mathrm{2}{x}} }\:{dx}\:=\:−\int\:{x}^{\mathrm{3}} \mathrm{cos}\:{x}\:{dx} \\ $$$${v}\left({x}\right)\:=\:\int\:\frac{\left({x}^{\mathrm{2}} {e}^{−{x}} \mathrm{cos}\:{x}\right)\left({e}^{−{x}} \right)}{{e}^{−\mathrm{2}{x}} }\:{dx}\:=\:\int\:{x}^{\mathrm{2}} \mathrm{cos}\:{x}\:{dx} \\ $$$$\Rightarrow\:{y}_{{p}} \left({x}\right)\:=\:... \\ $$

Commented by i jagooll last updated on 09/May/20

tobe continue sir

$$\mathrm{tobe}\:\mathrm{continue}\:\mathrm{sir} \\ $$

Commented by Joel578 last updated on 09/May/20

I think the integrals are easy for someone that asking an ODE problem, so I leave the rest for you

$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{integrals}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{for}\:\mathrm{someone}\:\mathrm{that}\:\mathrm{asking} \\ $$$$\mathrm{an}\:\mathrm{ODE}\:\mathrm{problem},\:\mathrm{so}\:\mathrm{I}\:\mathrm{leave}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{for}\:\mathrm{you} \\ $$

Commented by Joel578 last updated on 09/May/20

������

Commented by i jagooll last updated on 09/May/20

��������

Commented by i jagooll last updated on 09/May/20

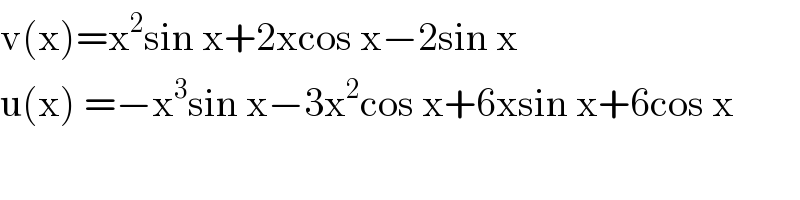
v(x)=x^2 sin x+2xcos x−2sin x u(x) =−x^3 sin x−3x^2 cos x+6xsin x+6cos x

$$\mathrm{v}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}+\mathrm{2xcos}\:\mathrm{x}−\mathrm{2sin}\:\mathrm{x} \\ $$$$\mathrm{u}\left(\mathrm{x}\right)\:=−\mathrm{x}^{\mathrm{3}} \mathrm{sin}\:\mathrm{x}−\mathrm{3x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{x}+\mathrm{6xsin}\:\mathrm{x}+\mathrm{6cos}\:\mathrm{x} \\ $$

Answered by niroj last updated on 09/May/20

PI = (( x^2 e^(−x) cos x)/(D^2 +2D+1)) = e^(−x) (( x^2 cos x)/(−1+2D+1)) = e^(−x) (( x^2 cos x)/(2D)) = (e^(−x) /2)∫x^2 cos x dx x^2 (sin x)−∫2x( sin x )dx x^2 sin x−2[ x (−cos x) −∫1.(−cosx) dx] x^2 sin x +2x cosx+2sin x . PI= (e^(−x) /2)(x^2 sin x+2xcos x+2 sinx) = e^(−x) ((1/2)x^2 sin x+ x cos x+ sin x).

$$\:\:\:\mathrm{PI}\:=\:\frac{\:\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{cos}\:\mathrm{x}}{\mathrm{D}^{\mathrm{2}} +\mathrm{2D}+\mathrm{1}}\: \\ $$$$\:\:\:\:=\:\mathrm{e}^{−\mathrm{x}} \:\frac{\:\mathrm{x}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{x}}{−\mathrm{1}+\mathrm{2D}+\mathrm{1}} \\ $$$$\:\:\:\:=\:\mathrm{e}^{−\mathrm{x}} \frac{\:\mathrm{x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{x}}{\mathrm{2D}} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\int\mathrm{x}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx} \\ $$$$\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \left(\mathrm{sin}\:\mathrm{x}\right)−\int\mathrm{2x}\left(\:\mathrm{sin}\:\mathrm{x}\:\right)\mathrm{dx} \\ $$$$\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}−\mathrm{2}\left[\:\mathrm{x}\:\left(−\mathrm{cos}\:\mathrm{x}\right)\:−\int\mathrm{1}.\left(−\mathrm{cosx}\right)\:\mathrm{dx}\right] \\ $$$$\:\:\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\:+\mathrm{2x}\:\mathrm{cosx}+\mathrm{2sin}\:\mathrm{x}\:. \\ $$$$\:\mathrm{PI}=\:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}+\mathrm{2xcos}\:\mathrm{x}+\mathrm{2}\:\mathrm{sinx}\right) \\ $$$$\:\:\:\:=\:\mathrm{e}^{−\mathrm{x}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{x}+\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}+\:\mathrm{sin}\:\mathrm{x}\right). \\ $$$$\:\: \\ $$$$\:\: \\ $$$$ \\ $$

Commented by i jagooll last updated on 09/May/20

I have a lot to learn in this way sir ������

Commented by niroj last updated on 09/May/20

you can solve by other method also like using by variation of parameter.

$$\:\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{other}\:\mathrm{method}\:\mathrm{also} \\ $$$$\:\mathrm{like}\:\mathrm{using}\:\mathrm{by}\:\mathrm{variation}\:\mathrm{of}\:\mathrm{parameter}. \\ $$

Answered by niroj last updated on 09/May/20

By the help of variation parametrs, (D^2 +2D+1)y= x^2 e^(−x) cos x A.E. , m^2 +2m+1=0 (m+1)^2 =0 m=−1, −1 CF= e^(−x) (C_(1 ) +C_2 x) =C_1 e^(−x) + C_2 xe^(−x) PI = −y_1 ∫ ((y_2 xdx)/w) +y_2 ∫ ((y_1 xdx)/w) y_1 = e^(−x) , y_2 =x e^(−x) , Wronskian^′ s determinants: W= determinant (((y_1 y_2 )),((y_1 ^′ y_2 ^′ ))) = determinant ((( e^(−x) e^(−x) x)),((−e^(−x) e^(−x) −xe^(−x) ))) w=e^(−x) (e^(−x) −xe^(−x) )+(e^(−x) x.e^(−x) ) = e^(−2x) −xe^(−2x) +xe^(−2x) = e^(−2x) PI = −e^(−x) ∫(( x e^(−x) x^2 e^(−x) cos x dx)/e^(−2x) ) + xe^(−x) ∫ ((e^(−x) x^2 e^(−x) cos x dx)/e^(−2x) ) = −e^(−x) ∫x^3 cos x dx +x e^(−x) ∫x^2 cos xdx now can get easily....

$$\:\mathrm{By}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{variation}\:\mathrm{parametrs}, \\ $$$$\:\:\left(\mathrm{D}^{\mathrm{2}} +\mathrm{2D}+\mathrm{1}\right)\mathrm{y}=\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\:\mathrm{A}.\mathrm{E}.\:,\:\mathrm{m}^{\mathrm{2}} +\mathrm{2m}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{m}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{m}=−\mathrm{1},\:−\mathrm{1} \\ $$$$\:\mathrm{CF}=\:\mathrm{e}^{−\mathrm{x}} \left(\mathrm{C}_{\mathrm{1}\:} +\mathrm{C}_{\mathrm{2}} \mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{C}_{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} +\:\mathrm{C}_{\mathrm{2}} \mathrm{xe}^{−\mathrm{x}} \\ $$$$\:\:\mathrm{PI}\:=\:−\mathrm{y}_{\mathrm{1}} \int\:\frac{\mathrm{y}_{\mathrm{2}} \:\mathrm{xdx}}{\mathrm{w}}\:+\mathrm{y}_{\mathrm{2}} \int\:\frac{\mathrm{y}_{\mathrm{1}} \:\mathrm{xdx}}{\mathrm{w}} \\ $$$$\:\:\:\:\mathrm{y}_{\mathrm{1}} =\:\mathrm{e}^{−\mathrm{x}} \:,\:\:\:\:\:\mathrm{y}_{\mathrm{2}} =\mathrm{x}\:\mathrm{e}^{−\mathrm{x}} \:,\: \\ $$$$\:\:\:\mathrm{Wronskian}^{'} \mathrm{s}\:\mathrm{determinants}: \\ $$$$\:\:\mathrm{W}=\:\begin{vmatrix}{\mathrm{y}_{\mathrm{1}} \:\:\:\:\:\:\:\:\mathrm{y}_{\mathrm{2}} }\\{\mathrm{y}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\mathrm{y}_{\mathrm{2}} ^{'} }\end{vmatrix} \\ $$$$\:\:\:\:\:=\:\begin{vmatrix}{\:\mathrm{e}^{−\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} \mathrm{x}}\\{−\mathrm{e}^{−\mathrm{x}} \:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} }\end{vmatrix} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\mathrm{w}=\mathrm{e}^{−\mathrm{x}} \:\left(\mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} \right)+\left(\mathrm{e}^{−\mathrm{x}} \mathrm{x}.\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{e}^{−\mathrm{2x}} −\mathrm{xe}^{−\mathrm{2x}} +\mathrm{xe}^{−\mathrm{2x}} \\ $$$$\:\:\:\:\:=\:\mathrm{e}^{−\mathrm{2x}} \\ $$$$\:\:\:\mathrm{PI}\:=\:−\mathrm{e}^{−\mathrm{x}} \:\int\frac{\:\mathrm{x}\:\mathrm{e}^{−\mathrm{x}} \mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{e}^{−\mathrm{2x}} }\:+\:\mathrm{xe}^{−\mathrm{x}} \int\:\frac{\mathrm{e}^{−\mathrm{x}} \:\:\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{e}^{−\mathrm{2x}} } \\ $$$$\:\:=\:\:−\mathrm{e}^{−\mathrm{x}} \int\mathrm{x}^{\mathrm{3}} \mathrm{cos}\:\mathrm{x}\:\:\mathrm{dx}\:+\mathrm{x}\:\mathrm{e}^{−\mathrm{x}} \int\mathrm{x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{xdx} \\ $$$$\:\:\mathrm{now}\:\mathrm{can}\:\mathrm{get}\:\mathrm{easily}.... \\ $$$$\:\:\:\:\:\: \\ $$

Commented by john santu last updated on 09/May/20

great...cheer ������

Terms of Service

Privacy Policy

Contact: info@tinkutara.com