
Question Number 9306 by tawakalitu last updated on 29/Nov/16
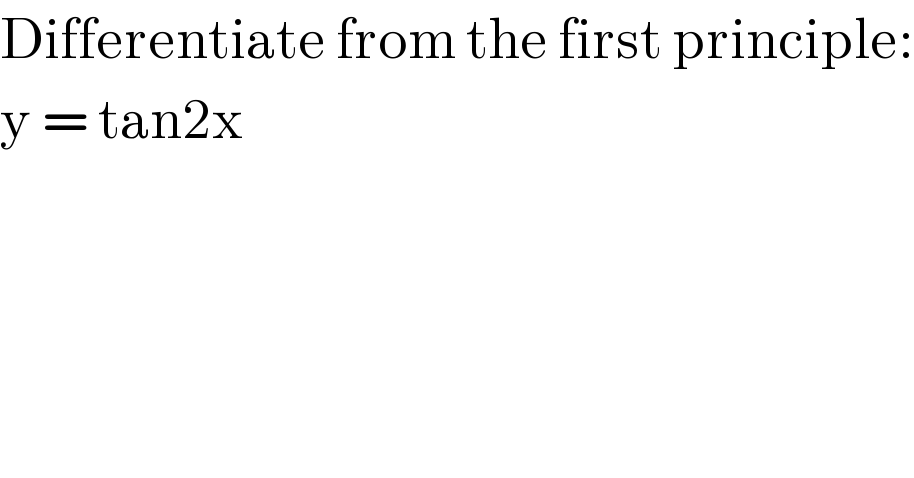
$$\mathrm{Differentiate}\:\mathrm{from}\:\mathrm{the}\:\mathrm{first}\:\mathrm{principle}: \\ $$$$\mathrm{y}\:=\:\mathrm{tan2x} \\ $$
Answered by mrW last updated on 30/Nov/16
![y(x)=tan (2x) y(x+h)=tan (2x+2h)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h))) y(x+h)−y(x)=((tan (2x)+tan (2h))/(1−tan (2x)×tan (2h)))−tan (2x) =((tan (2x)+tan (2h)−tan (2x)+tan^2 (2x)×tan (2h))/(1−tan (2x)×tan (2h))) =((1+tan^2 (2x))/((1/(tan (2h)))−tan (2x))) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/((h/(tan (2h)))−tan (2x)×h)) lim_(h→0) (h/(tan (2h)))=lim_(h→0) (1/(2×((tan (2h))/(2h))))=(1/2) lim_(h→0) tan (2x)×h=0 (dy/dx)=lim_(h→0) ((y(x+h)−y(x))/h)=((1+tan^2 (2x))/(1/2))=2[1+tan^2 (2x)]=(2/(cos^2 (2x)))](Q9308.png)
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{tan}\:\left(\mathrm{2x}\right) \\ $$$$\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)=\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{2h}\right)=\frac{\mathrm{tan}\:\left(\mathrm{2x}\right)+\mathrm{tan}\:\left(\mathrm{2h}\right)}{\mathrm{1}−\mathrm{tan}\:\left(\mathrm{2x}\right)×\mathrm{tan}\:\left(\mathrm{2h}\right)} \\ $$$$\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{tan}\:\left(\mathrm{2x}\right)+\mathrm{tan}\:\left(\mathrm{2h}\right)}{\mathrm{1}−\mathrm{tan}\:\left(\mathrm{2x}\right)×\mathrm{tan}\:\left(\mathrm{2h}\right)}−\mathrm{tan}\:\left(\mathrm{2x}\right) \\ $$$$=\frac{\mathrm{tan}\:\left(\mathrm{2x}\right)+\mathrm{tan}\:\left(\mathrm{2h}\right)−\mathrm{tan}\:\left(\mathrm{2x}\right)+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2x}\right)×\mathrm{tan}\:\left(\mathrm{2h}\right)}{\mathrm{1}−\mathrm{tan}\:\left(\mathrm{2x}\right)×\mathrm{tan}\:\left(\mathrm{2h}\right)}\:\: \\ $$$$=\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2x}\right)}{\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{2h}\right)}−\mathrm{tan}\:\left(\mathrm{2x}\right)}\:\: \\ $$$$\frac{\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{y}\left(\mathrm{x}\right)}{\mathrm{h}}=\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2x}\right)}{\frac{\mathrm{h}}{\mathrm{tan}\:\left(\mathrm{2h}\right)}−\mathrm{tan}\:\left(\mathrm{2x}\right)×\mathrm{h}} \\ $$$$\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{h}}{\mathrm{tan}\:\left(\mathrm{2h}\right)}=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{tan}\:\left(\mathrm{2h}\right)}{\mathrm{2h}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{tan}\:\left(\mathrm{2x}\right)×\mathrm{h}=\mathrm{0} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{y}\left(\mathrm{x}\right)}{\mathrm{h}}=\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2x}\right)}{\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}\left[\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2x}\right)\right]=\frac{\mathrm{2}}{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{2x}\right)} \\ $$
Commented by tawakalitu last updated on 29/Nov/16

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
