Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 93173 by I want to learn more last updated on 11/May/20

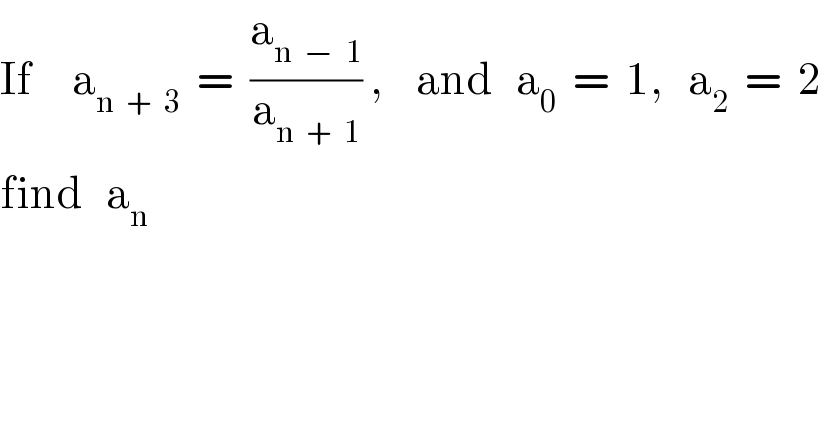
If a_(n + 3) = (a_(n − 1) /a_(n + 1) ) , and a_0 = 1, a_2 = 2 find a_n

$$\mathrm{If}\:\:\:\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{3}} \:\:=\:\:\frac{\mathrm{a}_{\mathrm{n}\:\:−\:\:\mathrm{1}} }{\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{1}} }\:,\:\:\:\:\mathrm{and}\:\:\:\mathrm{a}_{\mathrm{0}} \:\:=\:\:\mathrm{1},\:\:\:\mathrm{a}_{\mathrm{2}} \:\:=\:\:\mathrm{2} \\ $$$$\mathrm{find}\:\:\:\mathrm{a}_{\mathrm{n}} \\ $$

Answered by prakash jain last updated on 12/May/20

a_(n+3) =(a_(n−1) /a_(n+1) ) b_n =ln a_n ln a_(n+3) =ln a_(n−1) −ln a_(n+1) b_(n+3) =b_(n−1) −b_(n+1) b_(n+3) +b_(n+1) −b_(n−1) =0 Characteristic equation x^4 +x^2 −1=0 x^2 =((−1±(√5))/2) x=±(√((−1±(√5))/2)) x=±(√(((√5)−1)/2)) and ±i(√(((√5)+1)/2)) b_n =c_1 ((√((√(5−1))/2)))^n +c_2 (−(√(((√5)−1)/2)))^n +c_3 (i(√(((√5)+1)/2)))^n +c_4 (−i(√(((√5)+1)/2)))^n b_n =(1/2^(n/2) ){(c_1 +(−1)^n c_2 )((√5)−1)^(n/2) +i(c_3 +(−1)^n c_4 )((√5)+1)^(n/2) a_n =exp((1/2^(n/2) ){(c_1 +(−1)^n c_2 )((√5)−1)^(n/2) +i(c_3 +(−1)^n c_4 )((√5)+1)^(n/2) ) where c_(1,) c_2 ,c_3 and c_4 are arbitarary constants. You have only given two initial conditions. You need 4 to determine c_1 to c_4

$${a}_{{n}+\mathrm{3}} =\frac{{a}_{{n}−\mathrm{1}} }{{a}_{{n}+\mathrm{1}} } \\ $$$${b}_{{n}} =\mathrm{ln}\:{a}_{{n}} \\ $$$$\mathrm{ln}\:{a}_{{n}+\mathrm{3}} =\mathrm{ln}\:{a}_{{n}−\mathrm{1}} −\mathrm{ln}\:{a}_{{n}+\mathrm{1}} \\ $$$${b}_{{n}+\mathrm{3}} ={b}_{{n}−\mathrm{1}} −{b}_{{n}+\mathrm{1}} \\ $$$${b}_{{n}+\mathrm{3}} +{b}_{{n}+\mathrm{1}} −{b}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{Characteristic}\:\mathrm{equation} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}=\pm\sqrt{\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$$${x}=\pm\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\:\mathrm{and}\:\pm{i}\sqrt{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}} \\ $$$${b}_{{n}} ={c}_{\mathrm{1}} \left(\sqrt{\frac{\sqrt{\mathrm{5}−\mathrm{1}}}{\mathrm{2}}}\right)^{{n}} +{c}_{\mathrm{2}} \left(−\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\right)^{{n}} \\ $$$$\:\:\:\:\:\:\:\:+{c}_{\mathrm{3}} \left({i}\sqrt{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}}\right)^{{n}} +{c}_{\mathrm{4}} \left(−{i}\sqrt{\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}}\right)^{{n}} \\ $$$${b}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}/\mathrm{2}} }\left\{\left({c}_{\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} {c}_{\mathrm{2}} \right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{{n}/\mathrm{2}} +{i}\left({c}_{\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}} {c}_{\mathrm{4}} \right)\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{{n}/\mathrm{2}} \right. \\ $$$$\mathrm{a}_{{n}} =\mathrm{exp}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}/\mathrm{2}} }\left\{\left({c}_{\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} {c}_{\mathrm{2}} \right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{{n}/\mathrm{2}} +{i}\left({c}_{\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}} {c}_{\mathrm{4}} \right)\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{{n}/\mathrm{2}} \right)\right. \\ $$$$\mathrm{where}\:{c}_{\mathrm{1},} {c}_{\mathrm{2}} ,{c}_{\mathrm{3}} \:\mathrm{and}\:{c}_{\mathrm{4}} \:\mathrm{are}\:\mathrm{arbitarary} \\ $$$$\mathrm{constants}. \\ $$$$ \\ $$$$\mathrm{You}\:\mathrm{have}\:\mathrm{only}\:\mathrm{given}\:\mathrm{two}\:\mathrm{initial} \\ $$$$\mathrm{conditions}.\:\mathrm{You}\:\mathrm{need}\:\mathrm{4}\:\mathrm{to} \\ $$$$\mathrm{determine}\:{c}_{\mathrm{1}} \mathrm{to}\:{c}_{\mathrm{4}} \\ $$

Commented by prakash jain last updated on 12/May/20

exp(x)=e^x

$${exp}\left({x}\right)={e}^{{x}} \\ $$

Commented by I want to learn more last updated on 12/May/20

Thanks sir, i appreciate

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com