
Question and Answers Forum
Question Number 93193 by john santu last updated on 11/May/20
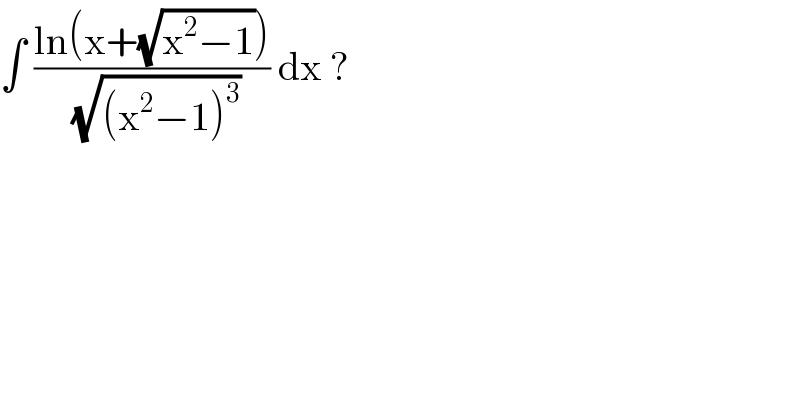
Commented by abdomathmax last updated on 14/May/20
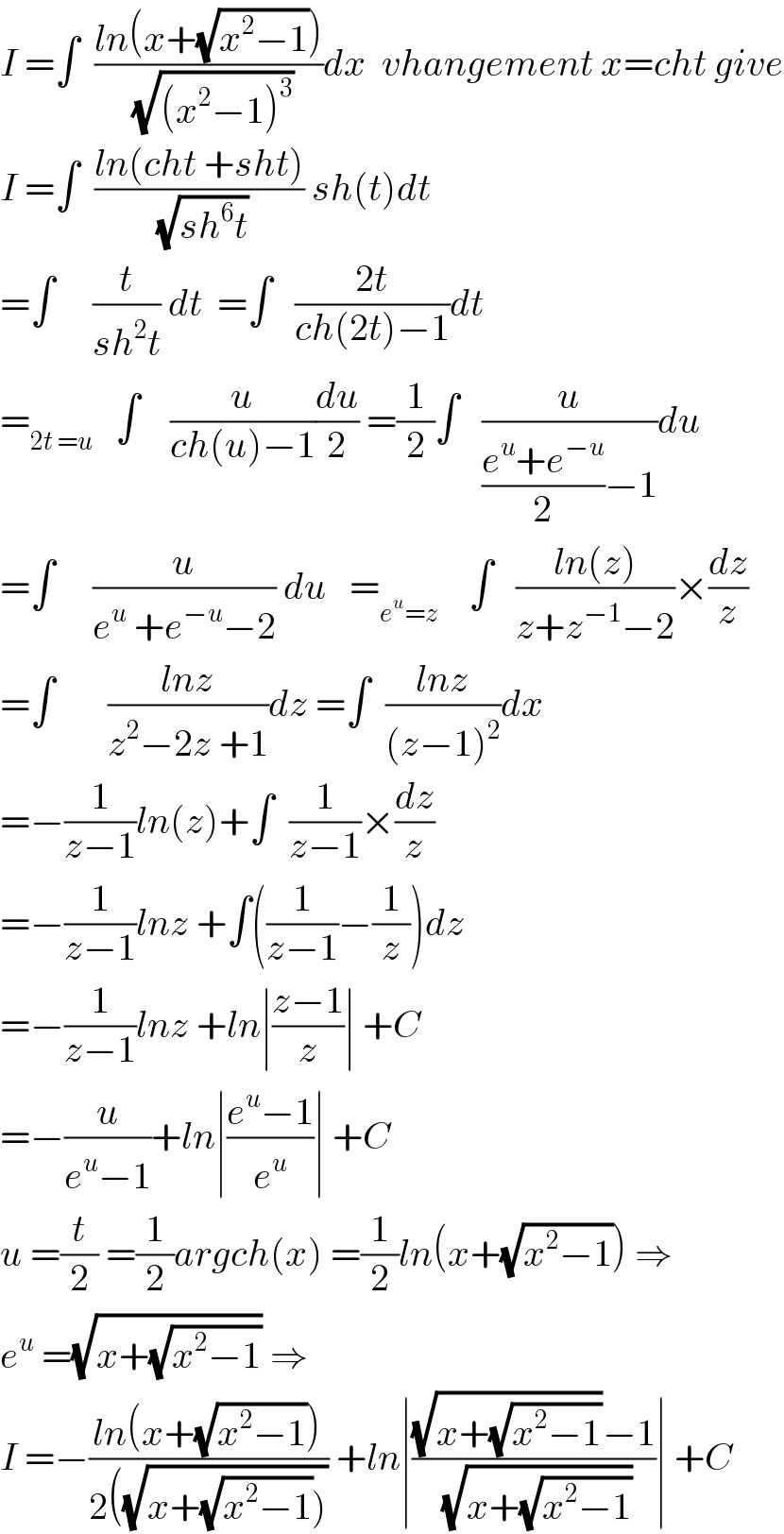
Answered by MJS last updated on 11/May/20
![∫((ln (x+(√(x^2 −1))))/((x^2 −1)^(3/2) ))dx= [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))dt] =4∫((t ln t)/((t^2 −1)^2 ))dt= by parts u=ln t → u′=(1/t) v′=((4t)/((t^2 −1)^2 )) → v=−(2/(t^2 −1)) =−((2ln t)/(t^2 −1))+2∫(dt/(t(t^2 −1)))= =−((2ln t)/(t^2 −1))+ln (t^2 −1) −2ln t = =−((2t^2 )/(t^2 −1))ln t +ln (t^2 −1) = =−((x+(√(x^2 −1)))/(√(x^2 −1)))ln (x+(√(x^2 −1))) +ln (x^2 −1+x(√(x^2 −1))) +C](Q93206.png)
Commented by john santu last updated on 12/May/20

| ||
Question and Answers Forum | ||
Question Number 93193 by john santu last updated on 11/May/20 | ||
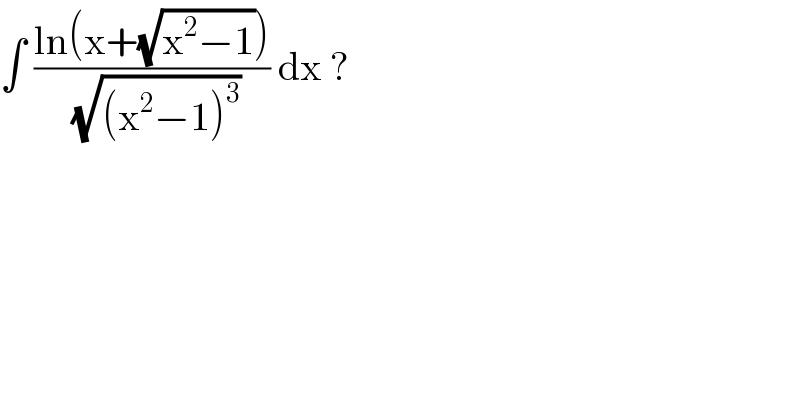 | ||
Commented by abdomathmax last updated on 14/May/20 | ||
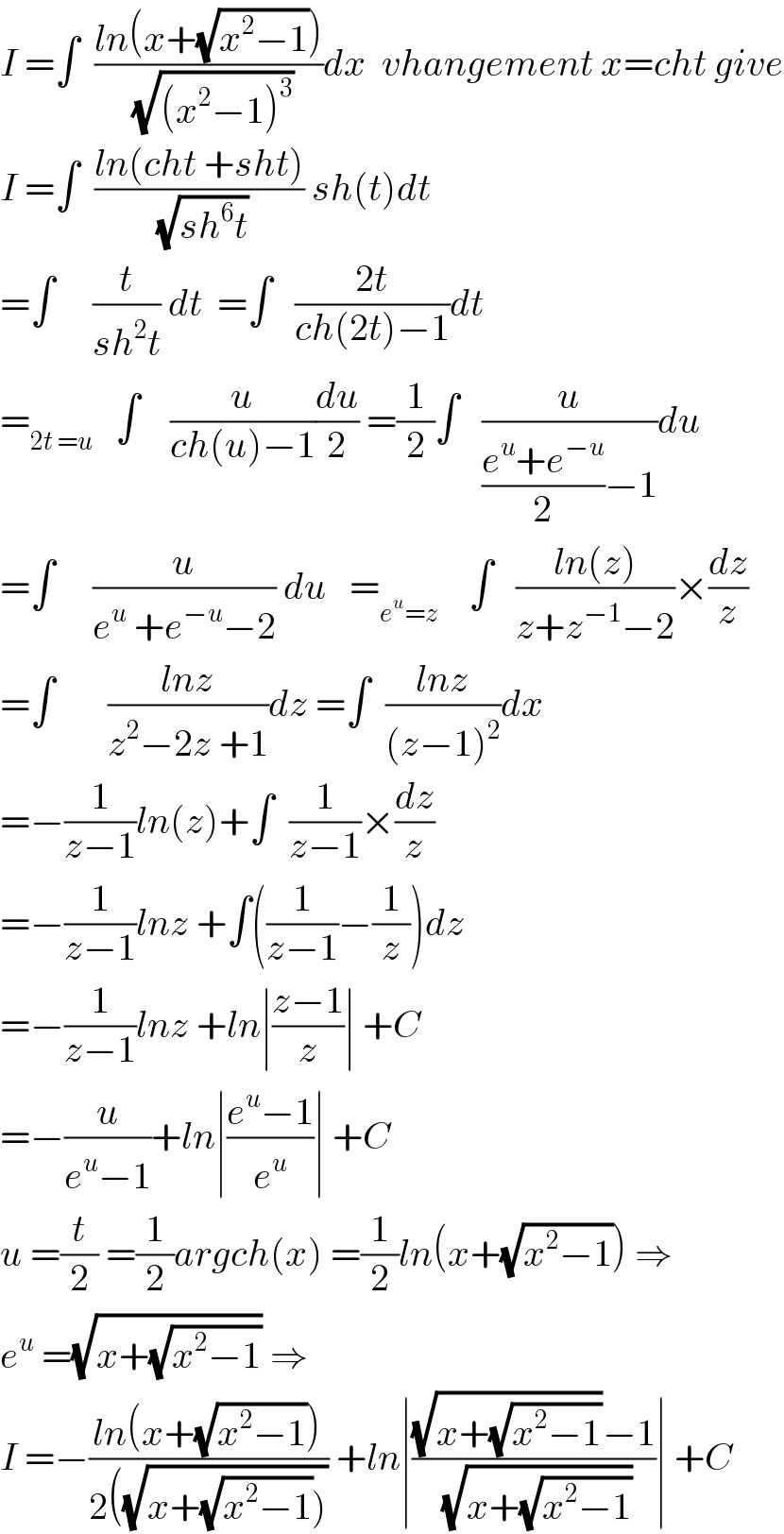 | ||
Answered by MJS last updated on 11/May/20 | ||
![∫((ln (x+(√(x^2 −1))))/((x^2 −1)^(3/2) ))dx= [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))dt] =4∫((t ln t)/((t^2 −1)^2 ))dt= by parts u=ln t → u′=(1/t) v′=((4t)/((t^2 −1)^2 )) → v=−(2/(t^2 −1)) =−((2ln t)/(t^2 −1))+2∫(dt/(t(t^2 −1)))= =−((2ln t)/(t^2 −1))+ln (t^2 −1) −2ln t = =−((2t^2 )/(t^2 −1))ln t +ln (t^2 −1) = =−((x+(√(x^2 −1)))/(√(x^2 −1)))ln (x+(√(x^2 −1))) +ln (x^2 −1+x(√(x^2 −1))) +C](Q93206.png) | ||
| ||
Commented by john santu last updated on 12/May/20 | ||
 | ||