Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 93200 by i jagooll last updated on 11/May/20

Commented by mathmax by abdo last updated on 11/May/20

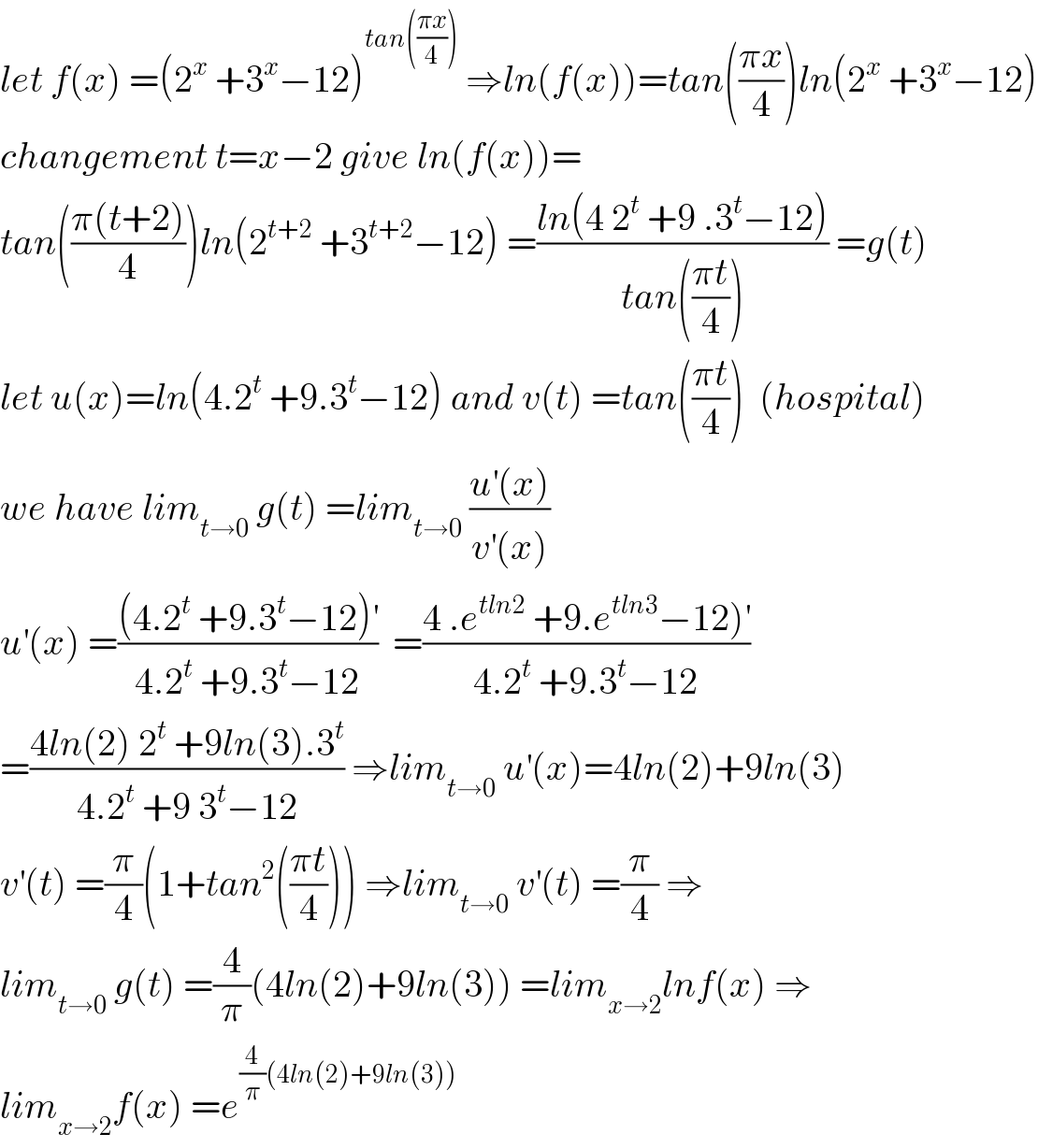
let f(x) =(2^x +3^x −12)^(tan(((πx)/4))) ⇒ln(f(x))=tan(((πx)/4))ln(2^x +3^x −12) changement t=x−2 give ln(f(x))= tan(((π(t+2))/4))ln(2^(t+2) +3^(t+2) −12) =((ln(4 2^t +9 .3^t −12))/(tan(((πt)/4)))) =g(t) let u(x)=ln(4.2^t +9.3^t −12) and v(t) =tan(((πt)/4)) (hospital) we have lim_(t→0) g(t) =lim_(t→0) ((u^′ (x))/(v^′ (x))) u^′ (x) =(((4.2^t +9.3^t −12)^′ )/(4.2^t +9.3^t −12)) =((4 .e^(tln2) +9.e^(tln3) −12)^′ )/(4.2^t +9.3^t −12)) =((4ln(2) 2^t +9ln(3).3^t )/(4.2^t +9 3^t −12)) ⇒lim_(t→0) u^′ (x)=4ln(2)+9ln(3) v^′ (t) =(π/4)(1+tan^2 (((πt)/4))) ⇒lim_(t→0) v^′ (t) =(π/4) ⇒ lim_(t→0) g(t) =(4/π)(4ln(2)+9ln(3)) =lim_(x→2) lnf(x) ⇒ lim_(x→2) f(x) =e^((4/π)(4ln(2)+9ln(3)))

$${let}\:{f}\left({x}\right)\:=\left(\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} −\mathrm{12}\right)^{{tan}\left(\frac{\pi{x}}{\mathrm{4}}\right)} \:\Rightarrow{ln}\left({f}\left({x}\right)\right)={tan}\left(\frac{\pi{x}}{\mathrm{4}}\right){ln}\left(\mathrm{2}^{{x}} \:+\mathrm{3}^{{x}} −\mathrm{12}\right) \\ $$$${changement}\:{t}={x}−\mathrm{2}\:{give}\:{ln}\left({f}\left({x}\right)\right)= \\ $$$${tan}\left(\frac{\pi\left({t}+\mathrm{2}\right)}{\mathrm{4}}\right){ln}\left(\mathrm{2}^{{t}+\mathrm{2}} \:+\mathrm{3}^{{t}+\mathrm{2}} −\mathrm{12}\right)\:=\frac{{ln}\left(\mathrm{4}\:\mathrm{2}^{{t}} \:+\mathrm{9}\:.\mathrm{3}^{{t}} −\mathrm{12}\right)}{{tan}\left(\frac{\pi{t}}{\mathrm{4}}\right)}\:={g}\left({t}\right) \\ $$$${let}\:{u}\left({x}\right)={ln}\left(\mathrm{4}.\mathrm{2}^{{t}} \:+\mathrm{9}.\mathrm{3}^{{t}} −\mathrm{12}\right)\:{and}\:{v}\left({t}\right)\:={tan}\left(\frac{\pi{t}}{\mathrm{4}}\right)\:\:\left({hospital}\right) \\ $$$${we}\:{have}\:{lim}_{{t}\rightarrow\mathrm{0}} \:{g}\left({t}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{u}^{'} \left({x}\right)}{{v}^{'} \left({x}\right)} \\ $$$${u}^{'} \left({x}\right)\:=\frac{\left(\mathrm{4}.\mathrm{2}^{{t}} \:+\mathrm{9}.\mathrm{3}^{{t}} −\mathrm{12}\right)^{'} }{\mathrm{4}.\mathrm{2}^{{t}} \:+\mathrm{9}.\mathrm{3}^{{t}} −\mathrm{12}}\:\:=\frac{\left.\mathrm{4}\:.{e}^{{tln}\mathrm{2}} \:+\mathrm{9}.{e}^{{tln}\mathrm{3}} −\mathrm{12}\right)^{'} }{\mathrm{4}.\mathrm{2}^{{t}} \:+\mathrm{9}.\mathrm{3}^{{t}} −\mathrm{12}} \\ $$$$=\frac{\mathrm{4}{ln}\left(\mathrm{2}\right)\:\mathrm{2}^{{t}} \:+\mathrm{9}{ln}\left(\mathrm{3}\right).\mathrm{3}^{{t}} }{\mathrm{4}.\mathrm{2}^{{t}} \:+\mathrm{9}\:\mathrm{3}^{{t}} −\mathrm{12}}\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:{u}^{'} \left({x}\right)=\mathrm{4}{ln}\left(\mathrm{2}\right)+\mathrm{9}{ln}\left(\mathrm{3}\right) \\ $$$${v}^{'} \left({t}\right)\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{\pi{t}}{\mathrm{4}}\right)\right)\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:{v}^{'} \left({t}\right)\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \:{g}\left({t}\right)\:=\frac{\mathrm{4}}{\pi}\left(\mathrm{4}{ln}\left(\mathrm{2}\right)+\mathrm{9}{ln}\left(\mathrm{3}\right)\right)\:={lim}_{{x}\rightarrow\mathrm{2}} {lnf}\left({x}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} {f}\left({x}\right)\:={e}^{\frac{\mathrm{4}}{\pi}\left(\mathrm{4}{ln}\left(\mathrm{2}\right)+\mathrm{9}{ln}\left(\mathrm{3}\right)\right)} \\ $$

Commented by john santu last updated on 12/May/20

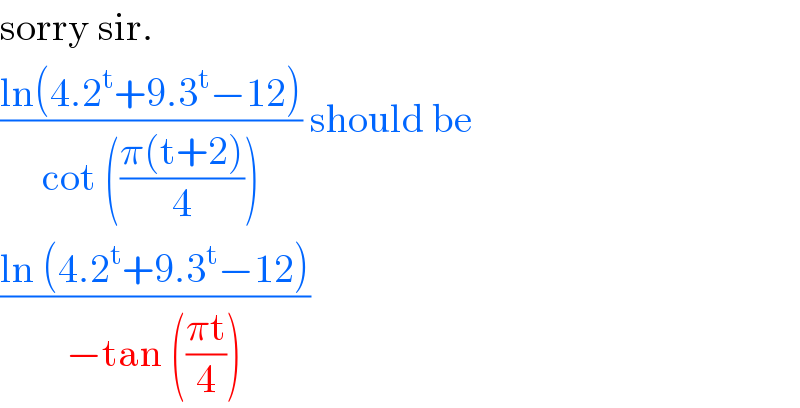
sorry sir. ((ln(4.2^t +9.3^t −12))/(cot (((π(t+2))/4)))) should be ((ln (4.2^t +9.3^t −12))/(−tan (((πt)/4))))

$$\mathrm{sorry}\:\mathrm{sir}.\: \\ $$$$\frac{\mathrm{ln}\left(\mathrm{4}.\mathrm{2}^{\mathrm{t}} +\mathrm{9}.\mathrm{3}^{\mathrm{t}} −\mathrm{12}\right)}{\mathrm{cot}\:\left(\frac{\pi\left(\mathrm{t}+\mathrm{2}\right)}{\mathrm{4}}\right)}\:\mathrm{should}\:\mathrm{be}\: \\ $$$$\frac{\mathrm{ln}\:\left(\mathrm{4}.\mathrm{2}^{\mathrm{t}} +\mathrm{9}.\mathrm{3}^{\mathrm{t}} −\mathrm{12}\right)}{−\mathrm{tan}\:\left(\frac{\pi\mathrm{t}}{\mathrm{4}}\right)}\: \\ $$

Commented by mathmax by abdo last updated on 12/May/20

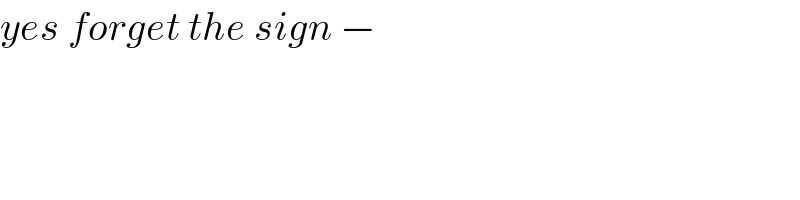
yes forget the sign −

$${yes}\:{forget}\:{the}\:{sign}\:− \\ $$

Answered by john santu last updated on 12/May/20

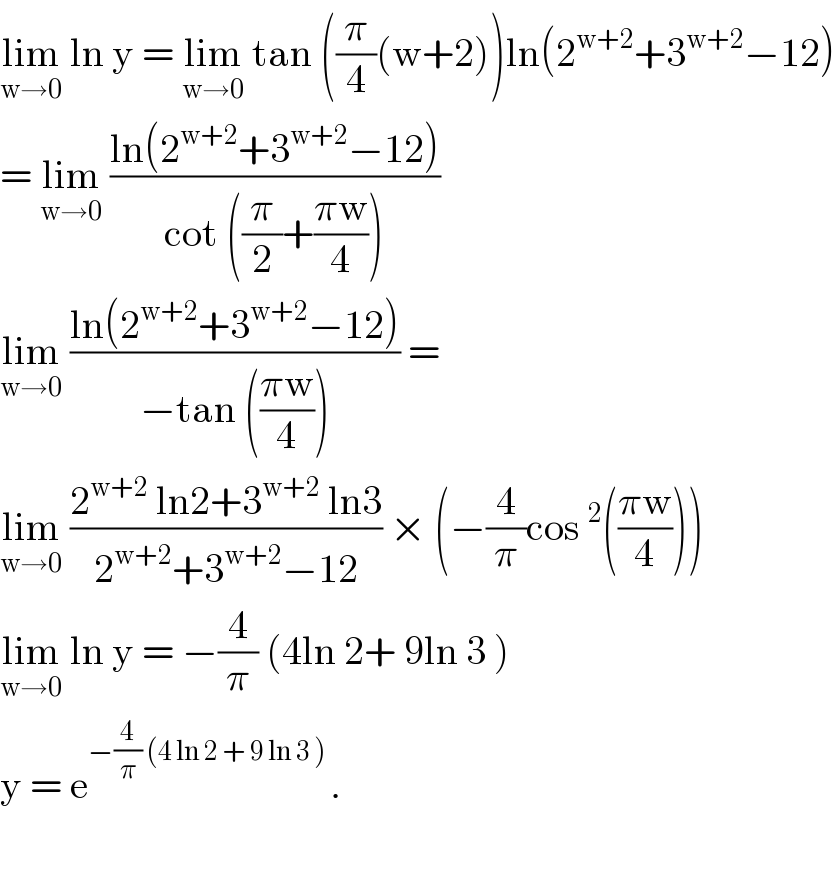
lim_(w→0) ln y = lim_(w→0) tan ((π/4)(w+2))ln(2^(w+2) +3^(w+2) −12) = lim_(w→0) ((ln(2^(w+2) +3^(w+2) −12))/(cot ((π/2)+((πw)/4)))) lim_(w→0) ((ln(2^(w+2) +3^(w+2) −12))/(−tan (((πw)/4)))) = lim_(w→0) ((2^(w+2) ln2+3^(w+2) ln3)/(2^(w+2) +3^(w+2) −12)) × (−(4/π)cos^2 (((πw)/4))) lim_(w→0) ln y = −(4/π) (4ln 2+ 9ln 3 ) y = e^(−(4/π) (4 ln 2 + 9 ln 3 ) ) .

$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\:\mathrm{y}\:=\:\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}\left(\mathrm{w}+\mathrm{2}\right)\right)\mathrm{ln}\left(\mathrm{2}^{\mathrm{w}+\mathrm{2}} +\mathrm{3}^{\mathrm{w}+\mathrm{2}} −\mathrm{12}\right) \\ $$$$=\:\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{2}^{\mathrm{w}+\mathrm{2}} +\mathrm{3}^{\mathrm{w}+\mathrm{2}} −\mathrm{12}\right)}{\mathrm{cot}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\pi\mathrm{w}}{\mathrm{4}}\right)} \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{2}^{\mathrm{w}+\mathrm{2}} +\mathrm{3}^{\mathrm{w}+\mathrm{2}} −\mathrm{12}\right)}{−\mathrm{tan}\:\left(\frac{\pi\mathrm{w}}{\mathrm{4}}\right)}\:= \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}^{\mathrm{w}+\mathrm{2}} \:\mathrm{ln2}+\mathrm{3}^{\mathrm{w}+\mathrm{2}} \:\mathrm{ln3}}{\mathrm{2}^{\mathrm{w}+\mathrm{2}} +\mathrm{3}^{\mathrm{w}+\mathrm{2}} −\mathrm{12}}\:×\:\left(−\frac{\mathrm{4}}{\pi}\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi\mathrm{w}}{\mathrm{4}}\right)\right) \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\:\mathrm{y}\:=\:−\frac{\mathrm{4}}{\pi}\:\left(\mathrm{4ln}\:\mathrm{2}+\:\mathrm{9ln}\:\mathrm{3}\:\right)\: \\ $$$$\mathrm{y}\:=\:\mathrm{e}^{−\frac{\mathrm{4}}{\pi}\:\left(\mathrm{4}\:\mathrm{ln}\:\mathrm{2}\:+\:\mathrm{9}\:\mathrm{ln}\:\mathrm{3}\:\right)\:} .\: \\ $$$$ \\ $$

Commented by i jagooll last updated on 12/May/20

yeahh...

$$\mathrm{yeahh}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com