Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 93239 by Ar Brandon last updated on 11/May/20

$$\mathrm{Calculate};$$$$i)\cos \left(\arctan x\right)$$$$ii)\cos \left(\arcsin x\right)$$$$iii)\tan \left(\arcsin x\right)$$

Commented by mathmax by abdo last updated on 12/May/20

$$1)vhangementarctanx=tgivex=tant\Rightarrow$$$$cos\left(arctanx\right)=cost=\sqrt{\frac{1}{1+{tan}^{2}t}}=\frac{1}{\sqrt{1+x^2}}$$$$2)letarcsinx=u\Rightarrow x=sinu\Rightarrow$$$$cos\left(arcsinx\right)=cosu=\sqrt{1-{sin}^{2}u}=\sqrt{1-x^2}$$$$3)letarcsinx=u\Rightarrow x=sinu\Rightarrow tan\left(arcsinx\right)=tanu$$$$=\frac{sinu}{cosu}=\frac{sinu}{\sqrt{1-{sin}^{2}u}}=\frac{x}{\sqrt{1-x^2}}$$

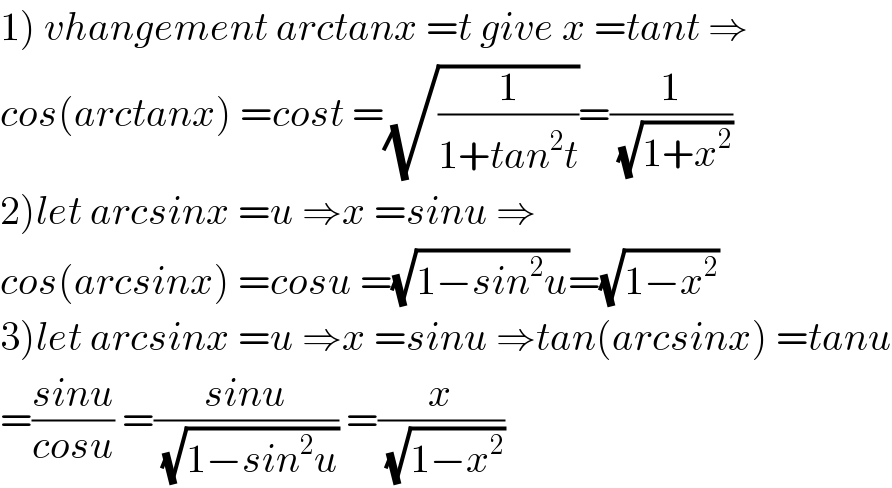
Commented by Ar Brandon last updated on 12/May/20

Thanks Mathmax ��

Commented by mathmax by abdo last updated on 12/May/20

$$youarewelcome.$$

Answered by hknkrc46 last updated on 12/May/20

$$i)\arctan x=u\Rightarrow \tan u=x\wedge \cos u=h=?$$$$\tan u=\frac{\sin u}{\cos u}=\frac{\sqrt{1-\cos {}^{2}u}}{\cos u}=\frac{\sqrt{1-h^2}}{h}=x$$$$\Rightarrow \sqrt{1-h^2}=hx\Rightarrow 1-h^2=h^2{x}^2$$$$\Rightarrow h^2{x}^2+h^2=1\Rightarrow h^2(x^2+1)=1$$$$\Rightarrow h^2=\frac{1}{x^2+1}\Rightarrow h=\frac{1}{\sqrt{x^2+1}}$$$$ii)\arcsin x=u\Rightarrow \sin u=x\wedge \cos u=?$$$$\cos u=\sqrt{\cos {}^{2}u}=\sqrt{1-\sin {}^{2}u}=\sqrt{1-x^2}$$$$iii)\arcsin x=u\Rightarrow \sin u=x\wedge \tan u=h=?$$$$h=\tan u=\frac{\sin u}{\cos u}=\frac{\sin u}{\sqrt{1-\sin {}^{2}u}}=\frac{x}{\sqrt{1-x^2}}$$

Commented by Ar Brandon last updated on 12/May/20

hknkrc46 Thank you sir ��

Answered by Rio Michael last updated on 12/May/20

$$\left(i\right)\cos \left(\arctan x\right)$$$$\mathrm{my}\mathrm{approach}$$$$\mathrm{let}\arctan x=u\Rightarrow \tan u=x$$$$\Rightarrow \frac{\sin u}{\cos u}=x$$$$\frac{{\sin }^{2}u}{{\cos }^{2}u}=x^2$$$$\Rightarrow \frac{{\sin }^{2}u}{{\cos }^{2}u}+1=x^2+1$$$$\mathrm{hence}\frac{{\sin }^{2}u+{\cos }^{2}u}{{\cos }^{2}u}=x^2+1$$$$\frac{1}{x^2+1}={\cos }^{2}u$$$$\Rightarrow \cos u=\sqrt{\frac{1}{x^2+1}}\mathrm{for}-\frac{\pi }{2}⩽x⩽\frac{\pi }{2}$$$$\mathrm{since}\mathrm{you}\mathrm{were}\mathrm{not}\mathrm{specific}.$$

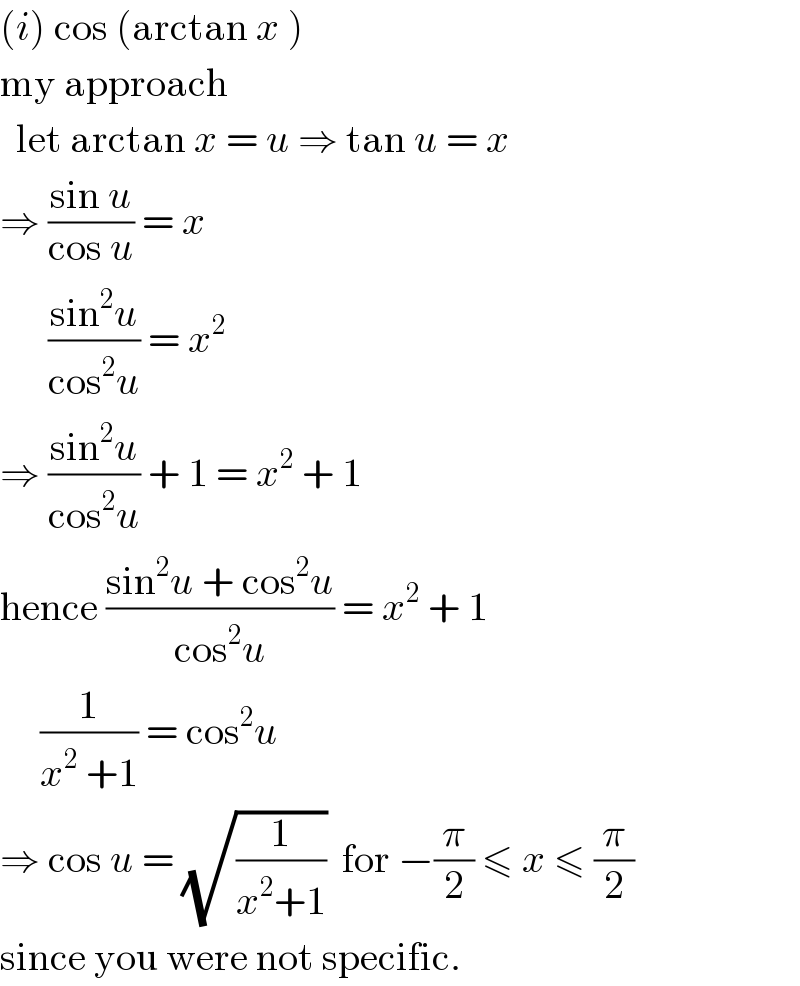
Commented by Ar Brandon last updated on 12/May/20

Thanks Mr Rio Michael. Good Day Sir ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com