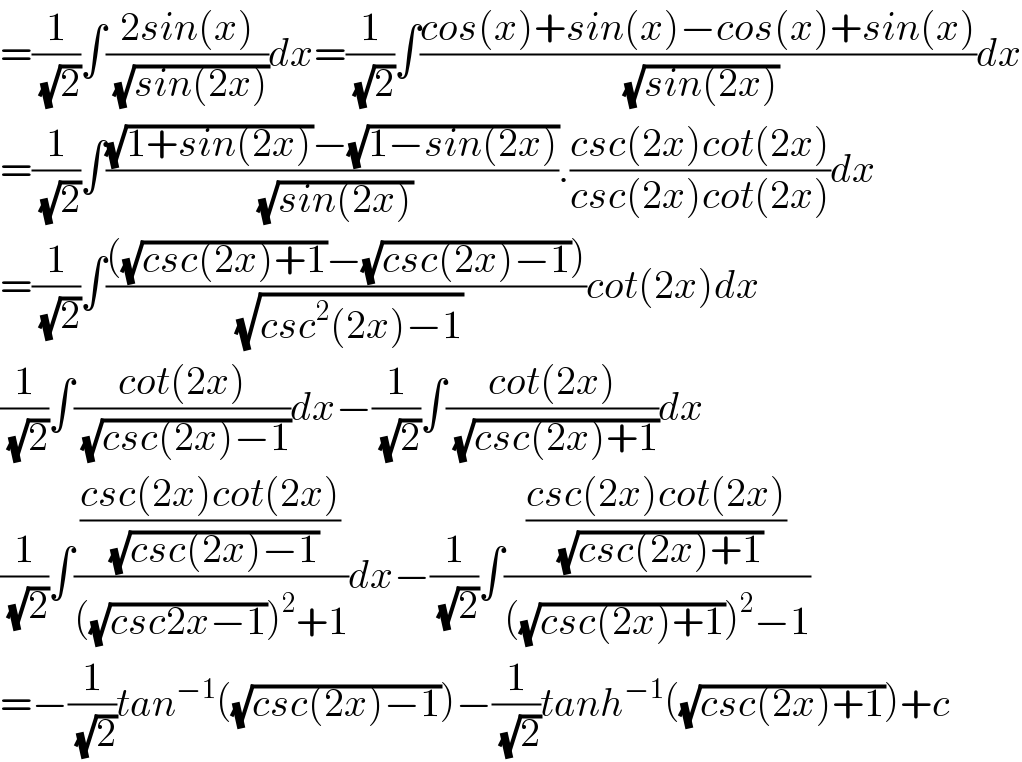Question and Answers Forum
Question Number 93304 by Shakhzod last updated on 12/May/20

Commented by john santu last updated on 12/May/20
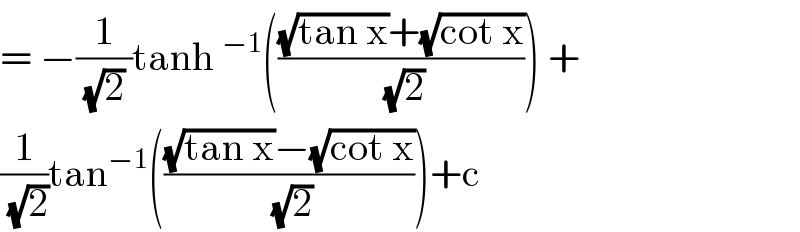
Commented by i jagooll last updated on 12/May/20
cooll man ����
Commented by i jagooll last updated on 12/May/20
![set u = (√(tan x)) , dx = ((2u du)/(u^4 +1)) ∫ (√(tan x)) dx = ∫ (2/(u^2 +(1/u^2 ))) du = ∫ ((1−(1/u))/((u+(1/u))^2 −2)) du + ∫ ((1+(1/u^2 ))/((u−(1/u))^2 +2)) du [ set u+(1/u) = tan q ], [ w=u−(1/u)] = ∫ (1/(q^2 −2)) dq + ∫ (1/(w^2 +2)) dw =−(1/(√2)) tanh^(−1) ((q/(√2))) +(1/(√2)) tan^(−1) ((w/(√2))) + c = −(1/(√2)) tanh^(−1) ((((√(tan x))+(√(cot x)))/(√2))) + (1/(√2)) tan^(−1) ((((√(tan x))−(√(cot x)))/(√2))) + c](Q93329.png)
Commented by M±th+et+s last updated on 12/May/20

Commented by mathmax by abdo last updated on 12/May/20

Answered by prakash jain last updated on 12/May/20

Commented by Shakhzod last updated on 12/May/20
Answered by M±th+et+s last updated on 12/May/20

Commented by Shakhzod last updated on 12/May/20

Answered by M±th+et+s last updated on 12/May/20
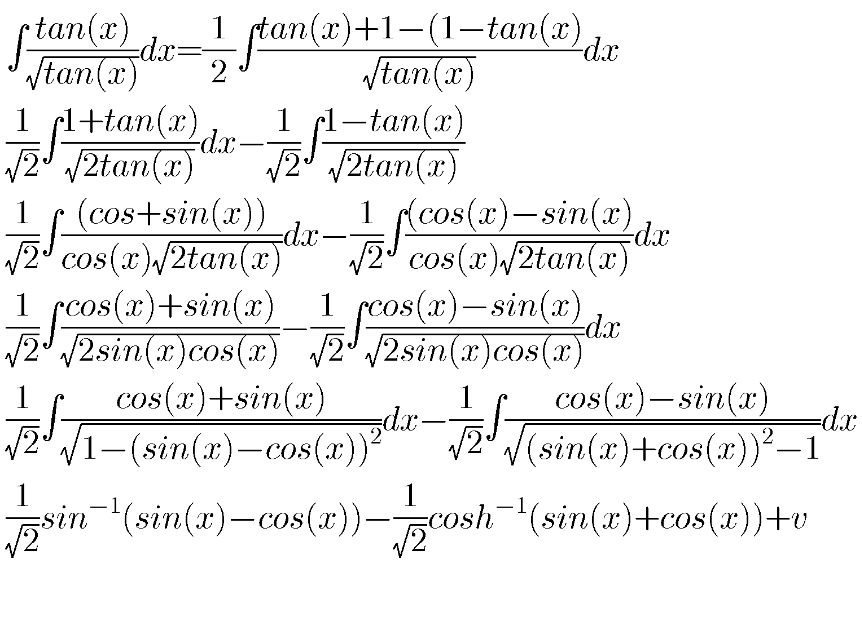
Answered by M±th+et+s last updated on 12/May/20

Answered by M±th+et+s last updated on 12/May/20