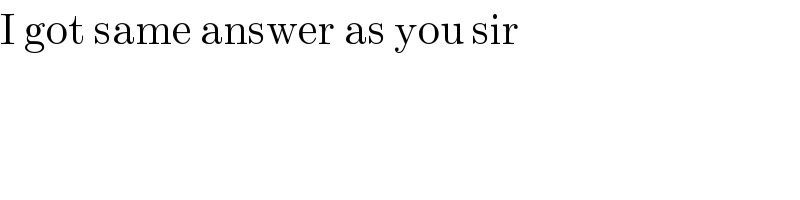Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 93340 by john santu last updated on 12/May/20

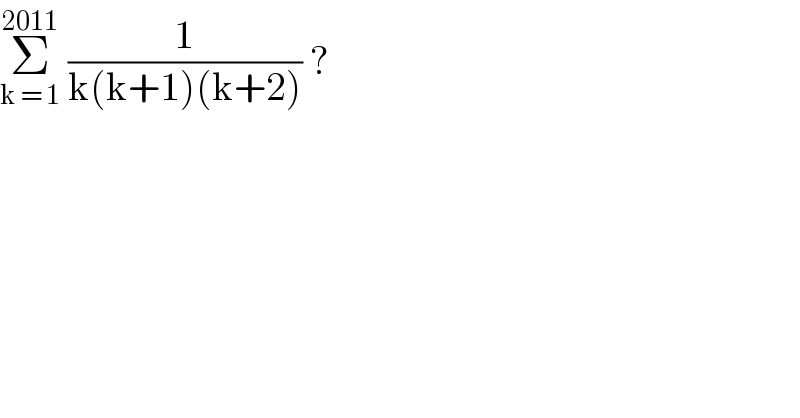
Σ_(k = 1) ^(2011) (1/(k(k+1)(k+2))) ?

$$\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{2011}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)}\:? \\ $$

Commented by mathmax by abdo last updated on 12/May/20

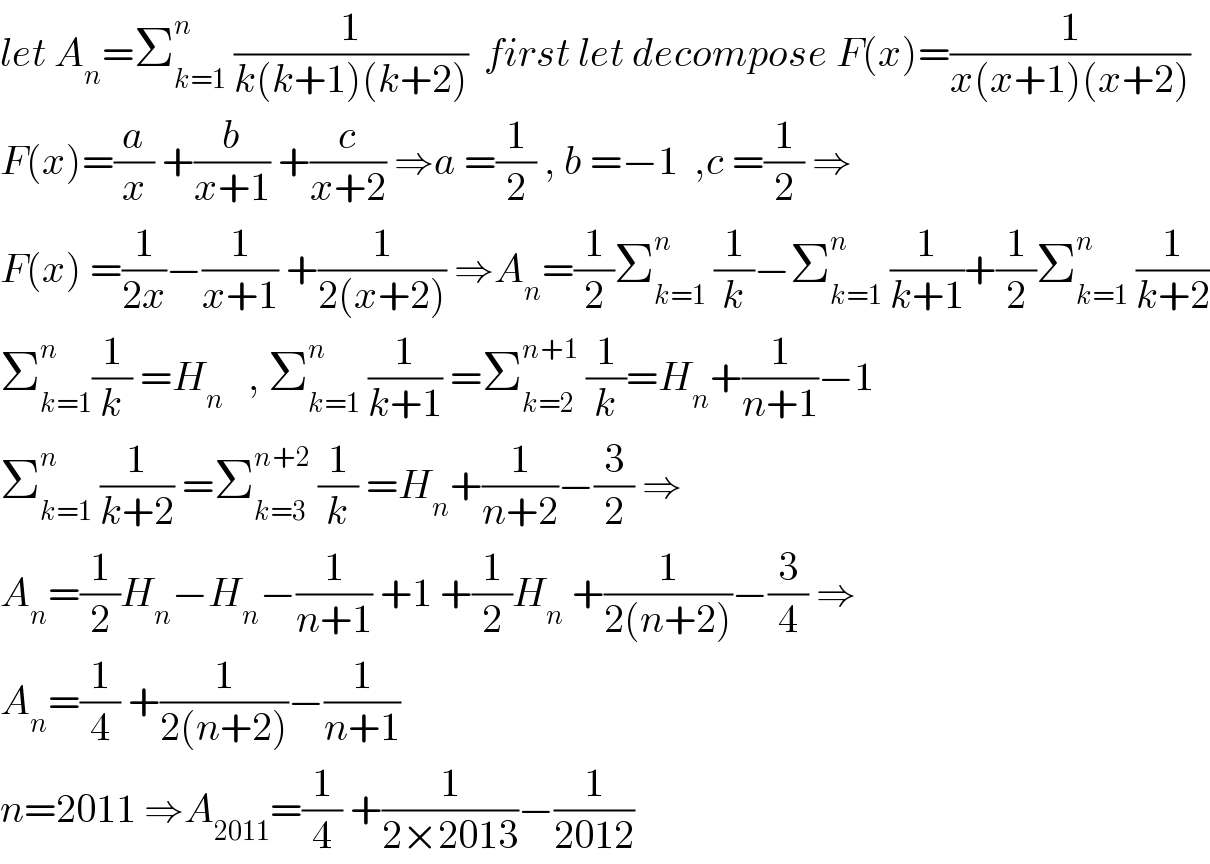
let A_n =Σ_(k=1) ^n (1/(k(k+1)(k+2))) first let decompose F(x)=(1/(x(x+1)(x+2))) F(x)=(a/x) +(b/(x+1)) +(c/(x+2)) ⇒a =(1/2) , b =−1 ,c =(1/2) ⇒ F(x) =(1/(2x))−(1/(x+1)) +(1/(2(x+2))) ⇒A_n =(1/2)Σ_(k=1) ^n (1/k)−Σ_(k=1) ^n (1/(k+1))+(1/2)Σ_(k=1) ^n (1/(k+2)) Σ_(k=1) ^n (1/k) =H_n , Σ_(k=1) ^n (1/(k+1)) =Σ_(k=2) ^(n+1) (1/k)=H_n +(1/(n+1))−1 Σ_(k=1) ^n (1/(k+2)) =Σ_(k=3) ^(n+2) (1/k) =H_n +(1/(n+2))−(3/2) ⇒ A_n =(1/2)H_n −H_n −(1/(n+1)) +1 +(1/2)H_n +(1/(2(n+2)))−(3/4) ⇒ A_n =(1/4) +(1/(2(n+2)))−(1/(n+1)) n=2011 ⇒A_(2011) =(1/4) +(1/(2×2013))−(1/(2012))

$${let}\:{A}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}\:\:{first}\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{{x}+\mathrm{1}}\:+\frac{{c}}{{x}+\mathrm{2}}\:\Rightarrow{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:,\:{b}\:=−\mathrm{1}\:\:,{c}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{2}\right)}\:\Rightarrow{A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{2}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{k}}\:={H}_{{n}} \:\:\:,\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}={H}_{{n}} +\frac{\mathrm{1}}{{n}+\mathrm{1}}−\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{2}}\:=\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{2}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} +\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} −{H}_{{n}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}\:+\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} \:+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{2}\right)}−\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{2}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${n}=\mathrm{2011}\:\Rightarrow{A}_{\mathrm{2011}} =\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{2013}}−\frac{\mathrm{1}}{\mathrm{2012}} \\ $$

Commented by prakash jain last updated on 12/May/20

I checked my answer but couldnt see any obvious error. Request your review.

$$\mathrm{I}\:\mathrm{checked}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{but} \\ $$$$\mathrm{couldnt}\:\mathrm{see}\:\mathrm{any}\:\mathrm{obvious}\:\mathrm{error}. \\ $$$$\mathrm{Request}\:\mathrm{your}\:\mathrm{review}. \\ $$

Commented by prakash jain last updated on 12/May/20

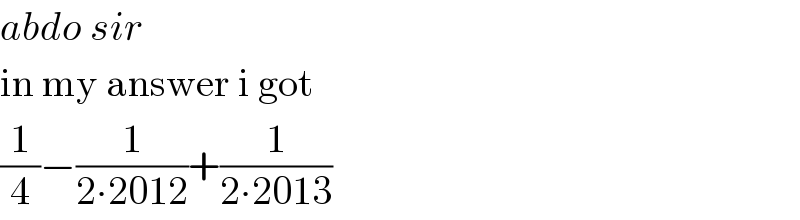
abdo sir in my answer i got (1/4)−(1/(2∙2012))+(1/(2∙2013))

$${abdo}\:{sir} \\ $$$$\mathrm{in}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{i}\:\mathrm{got} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2012}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2013}} \\ $$

Commented by Ar Brandon last updated on 12/May/20

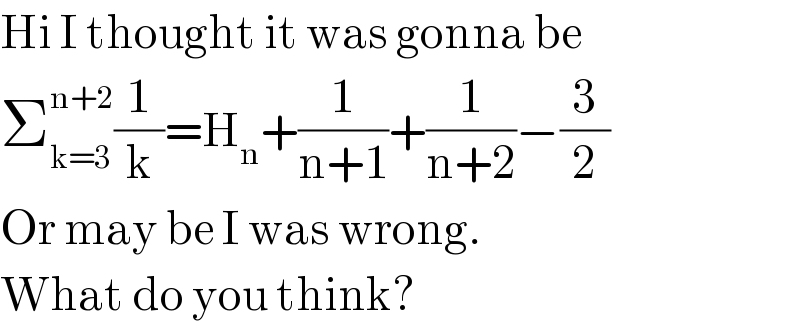
Hi I thought it was gonna be Σ_(k=3) ^(n+2) (1/k)=H_n +(1/(n+1))+(1/(n+2))−(3/2) Or may be I was wrong. What do you think?

$$\mathrm{Hi}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{was}\:\mathrm{gonna}\:\mathrm{be} \\ $$$$\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}+\mathrm{2}} \frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{Or}\:\mathrm{may}\:\mathrm{be}\:\mathrm{I}\:\mathrm{was}\:\mathrm{wrong}.\: \\ $$$$\mathrm{What}\:\mathrm{do}\:\mathrm{you}\:\mathrm{think}? \\ $$

Commented by turbo msup by abdo last updated on 12/May/20

that s what i find its correct.

$${that}\:{s}\:{what}\:{i}\:{find}\:{its}\:{correct}. \\ $$

Commented by I want to learn more last updated on 12/May/20

S_n = C − (1/(1.2)).(1/((n + 1)(n + 2))), put n = 1 ∴ S_1 = C − (1/(2(1 + 1)(1 + 2))), ⇒ (1/(1.2.3)) = C − (1/(2(2)(3))) ∴ (1/6) = C − (1/(12)), C = (1/6) + (1/(12)) = ((2 + 1)/(12)) = (3/(12)) = (1/4) ∴ S_n = (1/4) − (1/(2(n + 1)(n + 2))) ∴ S_(2011) = (1/4) − (1/(2(2011 + 1)(2011 + 2))) ∴ S_(2011) = (1/4) − (1/(2(2012)(2013))) ∴ S_(2011) = ((2025077)/(8100312))

$$\mathrm{S}_{\mathrm{n}} \:\:=\:\:\mathrm{C}\:\:−\:\:\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}}.\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{n}}\:+\:\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}\:+\:\mathrm{2}\right)},\:\:\:\:\:\:\mathrm{put}\:\:\boldsymbol{\mathrm{n}}\:\:=\:\:\mathrm{1} \\ $$$$\therefore\:\:\:\:\boldsymbol{\mathrm{S}}_{\mathrm{1}} \:\:\:=\:\:\:\boldsymbol{\mathrm{C}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}\:\:+\:\:\mathrm{1}\right)\left(\mathrm{1}\:\:+\:\:\mathrm{2}\right)},\:\:\:\:\Rightarrow\:\:\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\:\:\:=\:\:\boldsymbol{\mathrm{C}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}\right)\left(\mathrm{3}\right)} \\ $$$$\therefore\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{6}}\:\:\:=\:\:\:\boldsymbol{\mathrm{C}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{12}},\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{C}}\:\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{6}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{12}}\:\:\:=\:\:\:\frac{\mathrm{2}\:\:+\:\:\mathrm{1}}{\mathrm{12}}\:\:\:=\:\:\:\:\frac{\mathrm{3}}{\mathrm{12}}\:\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{n}}} \:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\boldsymbol{\mathrm{n}}\:\:+\:\:\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}\:\:+\:\:\mathrm{2}\right)} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}_{\mathrm{2011}} \:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2011}\:\:+\:\:\mathrm{1}\right)\left(\mathrm{2011}\:\:+\:\:\mathrm{2}\right)} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}_{\mathrm{2011}} \:\:=\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:−\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2012}\right)\left(\mathrm{2013}\right)} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}_{\mathrm{2011}} \:\:=\:\:\:\frac{\mathrm{2025077}}{\mathrm{8100312}} \\ $$

Commented by I want to learn more last updated on 12/May/20

I got the same thing as prakash jane

$$\mathrm{I}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{thing}\:\mathrm{as}\:\:\mathrm{prakash}\:\mathrm{jane} \\ $$

Answered by prakash jain last updated on 12/May/20

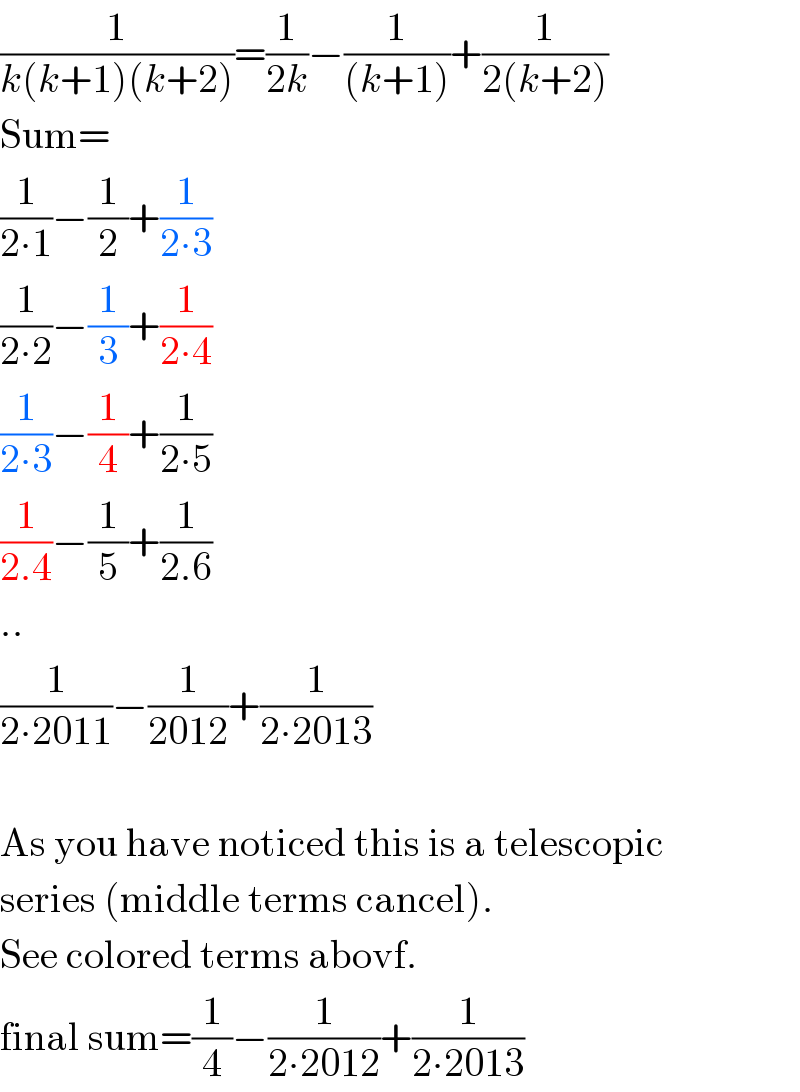
(1/(k(k+1)(k+2)))=(1/(2k))−(1/((k+1)))+(1/(2(k+2))) Sum= (1/(2∙1))−(1/2)+(1/(2∙3)) (1/(2∙2))−(1/3)+(1/(2∙4)) (1/(2∙3))−(1/4)+(1/(2∙5)) (1/(2.4))−(1/5)+(1/(2.6)) .. (1/(2∙2011))−(1/(2012))+(1/(2∙2013)) As you have noticed this is a telescopic series (middle terms cancel). See colored terms abovf. final sum=(1/4)−(1/(2∙2012))+(1/(2∙2013))

$$\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{2}{k}}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({k}+\mathrm{2}\right)} \\ $$$$\mathrm{Sum}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{5}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{6}} \\ $$$$.. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2011}}−\frac{\mathrm{1}}{\mathrm{2012}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2013}} \\ $$$$ \\ $$$$\mathrm{As}\:\mathrm{you}\:\mathrm{have}\:\mathrm{noticed}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{telescopic} \\ $$$$\mathrm{series}\:\left(\mathrm{middle}\:\mathrm{terms}\:\mathrm{cancel}\right). \\ $$$$\mathrm{See}\:\mathrm{colored}\:\mathrm{terms}\:\mathrm{abovf}. \\ $$$$\mathrm{final}\:\mathrm{sum}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2012}}+\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{2013}} \\ $$

Commented by I want to learn more last updated on 12/May/20

I got same answer as you sir

$$\mathrm{I}\:\mathrm{got}\:\mathrm{same}\:\mathrm{answer}\:\mathrm{as}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com