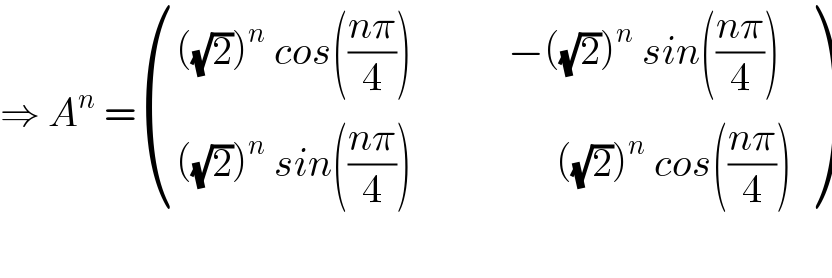Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 93415 by abdomathmax last updated on 13/May/20

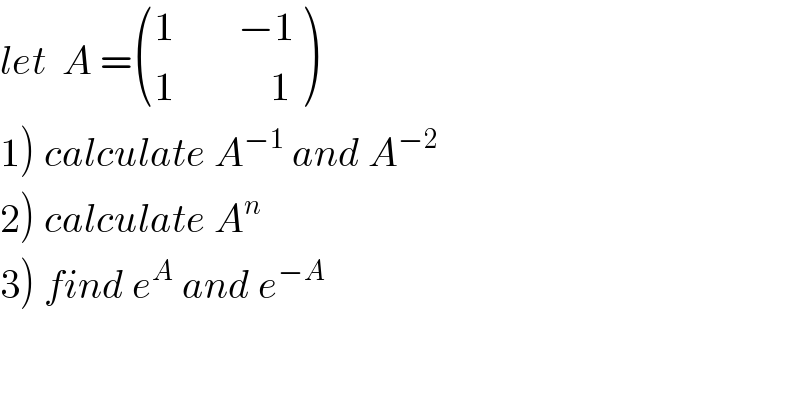
let A = (((1 −1)),((1 1)) ) 1) calculate A^(−1) and A^(−2) 2) calculate A^n 3) find e^A and e^(−A)

$${let}\:\:{A}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}^{−\mathrm{1}} \:{and}\:{A}^{−\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{A}^{{n}} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{e}^{{A}} \:{and}\:{e}^{−{A}} \\ $$

Commented by prakash jain last updated on 13/May/20

det(A−λI)= determinant (((1−λ),(−1)),(1,(1−λ))) =(1−λ)^2 +1=0 λ=1−i,1+i (i=(√(−1))) Eigenvector for λ=1−i (A−λI) [(x_1 ),(x_2 ) ]=0 ( [(1,(−1)),(1,1) ]− [((1−i),0),(0,(1−i)) ]) [(x_1 ),(x_2 ) ]=0 [(i,(−1)),(1,i) ] [(x_1 ),(x_2 ) ]=0 ix_1 −x_2 =0 x_1 +ix_2 =0 x_1 =1,x_2 =i ( [(1,(−1)),(1,1) ]− [((1+i),0),(0,(1+i)) ]) [(y_1 ),(y_2 ) ]=0 [((−i),(−1)),(1,(−i)) ] [(y_1 ),(y_2 ) ]=0 −iy_1 −y_2 =0 y_1 −iy_2 =0 y_1 =1, y_2 =−i S= [(1,1),((−i),i) ] S^(−1) = [((1/2),(i/2)),((1/2),(−i/2)) ] S^(−1) AS= [((1+i),0),(0,(1−i)) ] A=S [((1+i),0),(0,(1−i)) ]S^(−1) A^n =S [(((1+i)^n ),0),(0,((1−i)^n )) ]S^(−1) A^n = [(1,1),((−i),i) ] [(((1−i)^n ),0),(0,((1+i)^n )) ] [((1/2),(i/2)),((1/2),(−i/2)) ] =(1/2) [(((1−i)^n +(1+i)^n ),(−i((1−i)^n −(1+i))^n )),((i((1−i)^n −(1+i)^n )),((1−i)^n +(1+i)^n )) ]

$$\mathrm{det}\left({A}−\lambda{I}\right)=\begin{vmatrix}{\mathrm{1}−\lambda}&{−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}−\lambda}\end{vmatrix} \\ $$$$=\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\mathrm{1}−{i},\mathrm{1}+{i}\:\:\left({i}=\sqrt{−\mathrm{1}}\right) \\ $$$$\mathrm{Eigenvector}\:\mathrm{for}\:\lambda=\mathrm{1}−{i} \\ $$$$\left({A}−\lambda{I}\right)\begin{bmatrix}{{x}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} }\end{bmatrix}=\mathrm{0} \\ $$$$\left(\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}−\begin{bmatrix}{\mathrm{1}−{i}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}−{i}}\end{bmatrix}\right)\begin{bmatrix}{{x}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} }\end{bmatrix}=\mathrm{0} \\ $$$$\begin{bmatrix}{{i}}&{−\mathrm{1}}\\{\mathrm{1}}&{{i}}\end{bmatrix}\begin{bmatrix}{{x}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} }\end{bmatrix}=\mathrm{0} \\ $$$${ix}_{\mathrm{1}} −{x}_{\mathrm{2}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{ix}_{\mathrm{2}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{1},{x}_{\mathrm{2}} ={i} \\ $$$$\left(\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}−\begin{bmatrix}{\mathrm{1}+{i}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}+{i}}\end{bmatrix}\right)\begin{bmatrix}{{y}_{\mathrm{1}} }\\{{y}_{\mathrm{2}} }\end{bmatrix}=\mathrm{0} \\ $$$$\begin{bmatrix}{−{i}}&{−\mathrm{1}}\\{\mathrm{1}}&{−{i}}\end{bmatrix}\begin{bmatrix}{{y}_{\mathrm{1}} }\\{{y}_{\mathrm{2}} }\end{bmatrix}=\mathrm{0} \\ $$$$−{iy}_{\mathrm{1}} −{y}_{\mathrm{2}} =\mathrm{0} \\ $$$${y}_{\mathrm{1}} −{iy}_{\mathrm{2}} =\mathrm{0} \\ $$$${y}_{\mathrm{1}} =\mathrm{1},\:{y}_{\mathrm{2}} =−{i} \\ $$$${S}=\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−{i}}&{{i}}\end{bmatrix} \\ $$$${S}^{−\mathrm{1}} =\begin{bmatrix}{\mathrm{1}/\mathrm{2}}&{{i}/\mathrm{2}}\\{\mathrm{1}/\mathrm{2}}&{−{i}/\mathrm{2}}\end{bmatrix} \\ $$$${S}^{−\mathrm{1}} {AS}=\begin{bmatrix}{\mathrm{1}+{i}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}−{i}}\end{bmatrix} \\ $$$${A}={S}\begin{bmatrix}{\mathrm{1}+{i}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}−{i}}\end{bmatrix}{S}^{−\mathrm{1}} \\ $$$${A}^{{n}} ={S}\begin{bmatrix}{\left(\mathrm{1}+{i}\right)^{{n}} }&{\mathrm{0}}\\{\mathrm{0}}&{\left(\mathrm{1}−{i}\right)^{{n}} }\end{bmatrix}{S}^{−\mathrm{1}} \\ $$$${A}^{{n}} =\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−{i}}&{{i}}\end{bmatrix}\begin{bmatrix}{\left(\mathrm{1}−{i}\right)^{{n}} }&{\mathrm{0}}\\{\mathrm{0}}&{\left(\mathrm{1}+{i}\right)^{{n}} }\end{bmatrix}\begin{bmatrix}{\mathrm{1}/\mathrm{2}}&{{i}/\mathrm{2}}\\{\mathrm{1}/\mathrm{2}}&{−{i}/\mathrm{2}}\end{bmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{bmatrix}{\left(\mathrm{1}−{i}\right)^{{n}} +\left(\mathrm{1}+{i}\right)^{{n}} }&{−{i}\left(\left(\mathrm{1}−{i}\right)^{{n}} −\left(\mathrm{1}+{i}\right)\right)^{{n}} \:}\\{{i}\left(\left(\mathrm{1}−{i}\right)^{{n}} −\left(\mathrm{1}+{i}\right)^{{n}} \right)}&{\left(\mathrm{1}−{i}\right)^{{n}} +\left(\mathrm{1}+{i}\right)^{{n}} }\end{bmatrix} \\ $$

Commented by mathmax by abdo last updated on 13/May/20

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented by mathmax by abdo last updated on 13/May/20

1) p_c (x) =det(A−xI) = determinant (((1−x −1)),((1 1−x)))=(1−x)^2 +1 =x^2 −2x+2 csyley hamilton theorem ⇒A^2 −2A +2I =0 ⇒ A(A−2I) =−2I ⇒A×(−(1/2))(A−2I) =I ⇒ A is inversible and A^(−1) =−(1/2)A +I = (((−(1/2) (1/2))),((−(1/2) −(1/2))) )+ (((1 0)),((0 1)) ) A^(−1) = ((((1/2) (1/2))),((−(1/2) (1/2))) ) and A^(−2) =(A^(−1) )^2

$$\left.\mathrm{1}\right)\:{p}_{{c}} \left({x}\right)\:={det}\left({A}−{xI}\right)\:=\begin{vmatrix}{\mathrm{1}−{x}\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−{x}}\end{vmatrix}=\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\:\:\:{csyley}\:{hamilton}\:{theorem}\:\Rightarrow{A}^{\mathrm{2}} −\mathrm{2}{A}\:+\mathrm{2}{I}\:=\mathrm{0}\:\Rightarrow \\ $$$${A}\left({A}−\mathrm{2}{I}\right)\:=−\mathrm{2}{I}\:\Rightarrow{A}×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({A}−\mathrm{2}{I}\right)\:={I}\:\Rightarrow\:{A}\:{is}\:{inversible}\: \\ $$$${and}\:{A}^{−\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{2}}{A}\:+{I}\:=\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix}+\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{−\mathrm{1}} \:=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix}\:\:\:\:{and}\:{A}^{−\mathrm{2}} \:=\left({A}^{−\mathrm{1}} \right)^{\mathrm{2}} \\ $$

Commented by mathmax by abdo last updated on 13/May/20

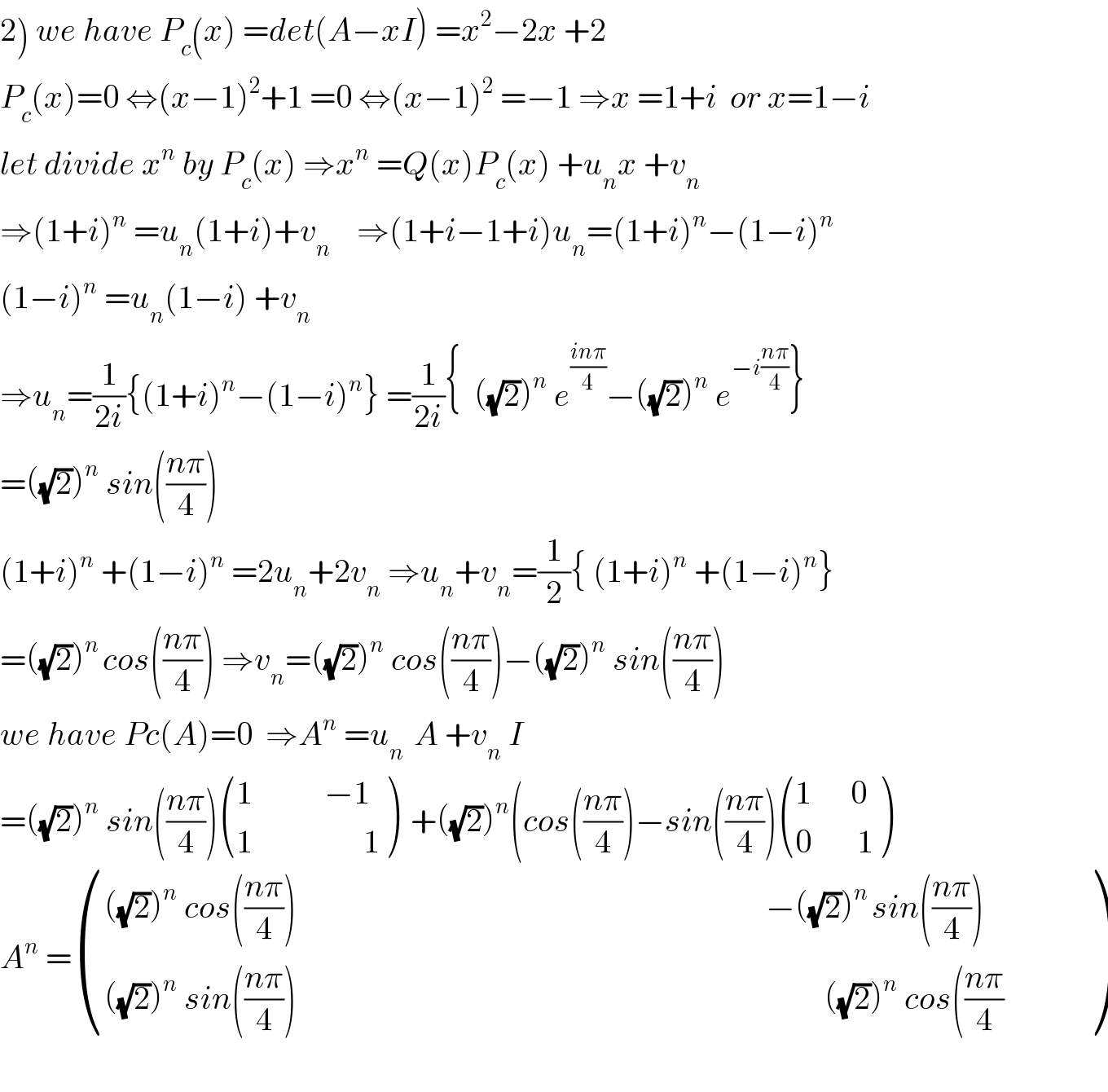
2) we have P_c (x) =det(A−xI) =x^2 −2x +2 P_c (x)=0 ⇔(x−1)^2 +1 =0 ⇔(x−1)^2 =−1 ⇒x =1+i or x=1−i let divide x^n by P_c (x) ⇒x^n =Q(x)P_c (x) +u_n x +v_n ⇒(1+i)^n =u_n (1+i)+v_n ⇒(1+i−1+i)u_n =(1+i)^n −(1−i)^n (1−i)^n =u_n (1−i) +v_n ⇒u_n =(1/(2i)){(1+i)^n −(1−i)^n } =(1/(2i)){ ((√2))^n e^((inπ)/4) −((√2))^n e^(−i((nπ)/4)) } =((√2))^n sin(((nπ)/4)) (1+i)^n +(1−i)^n =2u_n +2v_n ⇒u_n +v_n =(1/2){ (1+i)^n +(1−i)^n } =((√2))^(n ) cos(((nπ)/4)) ⇒v_n =((√2))^n cos(((nπ)/4))−((√2))^n sin(((nπ)/4)) we have Pc(A)=0 ⇒A^n =u_(n ) A +v_n I =((√2))^n sin(((nπ)/4)) (((1 −1)),((1 1)) ) +((√2))^n (cos(((nπ)/4))−sin(((nπ)/4)) (((1 0)),((0 1)) ) A^n = (((((√2))^n cos(((nπ)/4)) −((√2))^(n ) sin(((nπ)/4)))),((((√2))^n sin(((nπ)/4)) ((√2))^n cos(((nπ)/4) )) )

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{P}_{{c}} \left({x}\right)\:={det}\left({A}−{xI}\right)\:={x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{2} \\ $$$${P}_{{c}} \left({x}\right)=\mathrm{0}\:\Leftrightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\:=\mathrm{0}\:\Leftrightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:=−\mathrm{1}\:\Rightarrow{x}\:=\mathrm{1}+{i}\:\:{or}\:{x}=\mathrm{1}−{i} \\ $$$${let}\:{divide}\:{x}^{{n}} \:{by}\:{P}_{{c}} \left({x}\right)\:\Rightarrow{x}^{{n}} \:={Q}\left({x}\right){P}_{{c}} \left({x}\right)\:+{u}_{{n}} {x}\:+{v}_{{n}} \\ $$$$\Rightarrow\left(\mathrm{1}+{i}\right)^{{n}} \:={u}_{{n}} \left(\mathrm{1}+{i}\right)+{v}_{{n}} \:\:\:\:\Rightarrow\left(\mathrm{1}+{i}−\mathrm{1}+{i}\right){u}_{{n}} =\left(\mathrm{1}+{i}\right)^{{n}} −\left(\mathrm{1}−{i}\right)^{{n}} \\ $$$$\left(\mathrm{1}−{i}\right)^{{n}} \:={u}_{{n}} \left(\mathrm{1}−{i}\right)\:+{v}_{{n}} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\left(\mathrm{1}+{i}\right)^{{n}} −\left(\mathrm{1}−{i}\right)^{{n}} \right\}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} −\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−{i}\frac{{n}\pi}{\mathrm{4}}} \right\} \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right) \\ $$$$\left(\mathrm{1}+{i}\right)^{{n}} \:+\left(\mathrm{1}−{i}\right)^{{n}} \:=\mathrm{2}{u}_{{n}} +\mathrm{2}{v}_{{n}} \:\Rightarrow{u}_{{n}} +{v}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left(\mathrm{1}+{i}\right)^{{n}} \:+\left(\mathrm{1}−{i}\right)^{{n}} \right\} \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{n}\:} {cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:\Rightarrow{v}_{{n}} =\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right) \\ $$$${we}\:{have}\:{Pc}\left({A}\right)=\mathrm{0}\:\:\Rightarrow{A}^{{n}} \:={u}_{{n}\:} \:{A}\:+{v}_{{n}} \:{I} \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:+\left(\sqrt{\mathrm{2}}\right)^{{n}} \left({cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)−{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\right. \\ $$$${A}^{{n}} \:=\begin{pmatrix}{\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\sqrt{\mathrm{2}}\right)^{{n}\:} {sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)}\\{\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\right.}\end{pmatrix} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 13/May/20

⇒ A^n = (((((√2))^n cos(((nπ)/4)) −((√2))^n sin(((nπ)/4)))),((((√2))^n sin(((nπ)/4)) ((√2))^n cos(((nπ)/4)))) )

$$\Rightarrow\:{A}^{{n}} \:=\begin{pmatrix}{\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:\:\:\:\:\:\:\:\:\:\:\:−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)}\\{\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\right)}\end{pmatrix} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com