Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 93474 by Rio Michael last updated on 13/May/20

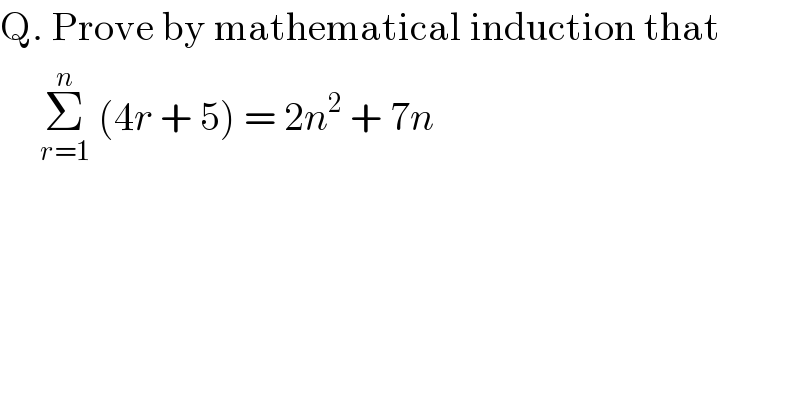
Q. Prove by mathematical induction that Σ_(r=1) ^n (4r + 5) = 2n^2 + 7n

$$\mathrm{Q}.\:\mathrm{Prove}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\mathrm{4}{r}\:+\:\mathrm{5}\right)\:=\:\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{7}{n}\: \\ $$

Answered by eswar150933 last updated on 13/May/20

Answered by allizzwell23 last updated on 13/May/20

P_1 : 4(1) + 5 = 9 = 2(1)^2 + 7(1) (true) Let n = k Σ_(r=1) ^n (4r + 5) = 2k^2 + 7k Assume n = k + 1 is true Σ_(r=1) ^n (4r + 5) + (4(r+1) + 5) = 2(k+1)^2 + 7(k+1) To prove the truth of n = k + 1 Σ_(r=1) ^n (4r + 5) + (4(r+1) + 5) = 2k^2 + 7k + (4(k+1) + 5) = 2k^2 + 7k + 4k + 4 + 5 = 2k^2 + 4k + 2 + 7k + 7 = 2(k^2 + 2k + 1) + 7(k + 1) = 2(k+1)^2 + 7(k+1) DONE ! 130520

$$\:\:\boldsymbol{{P}}_{\mathrm{1}} \::\:\mathrm{4}\left(\mathrm{1}\right)\:+\:\mathrm{5}\:=\:\mathrm{9}\:=\:\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{7}\left(\mathrm{1}\right)\:\:\:\:\:\:\left(\boldsymbol{\mathrm{true}}\right) \\ $$$$\:\:\boldsymbol{\mathrm{Let}}\:\boldsymbol{{n}}\:=\:\boldsymbol{{k}} \\ $$$$\:\:\:\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\mathrm{4}{r}\:+\:\mathrm{5}\right)\:=\:\mathrm{2}{k}^{\mathrm{2}} \:+\:\mathrm{7}{k}\: \\ $$$$\:\:\boldsymbol{\mathrm{Assume}}\:\boldsymbol{{n}}\:=\:\boldsymbol{{k}}\:+\:\mathrm{1}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{true}} \\ $$$$\:\:\:\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\mathrm{4}{r}\:+\:\mathrm{5}\right)\:+\:\left(\mathrm{4}\left({r}+\mathrm{1}\right)\:+\:\mathrm{5}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{7}\left({k}+\mathrm{1}\right)\: \\ $$$$\:\:\boldsymbol{\mathrm{To}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{truth}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{{n}}\:=\:\boldsymbol{{k}}\:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\mathrm{4}{r}\:+\:\mathrm{5}\right)\:+\:\left(\mathrm{4}\left({r}+\mathrm{1}\right)\:+\:\mathrm{5}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{k}^{\mathrm{2}} \:+\:\mathrm{7}{k}\:+\:\left(\mathrm{4}\left({k}+\mathrm{1}\right)\:+\:\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{k}^{\mathrm{2}} \:+\:\mathrm{7}{k}\:+\:\mathrm{4}{k}\:+\:\mathrm{4}\:+\:\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{k}^{\mathrm{2}} \:+\:\mathrm{4}{k}\:+\:\mathrm{2}\:+\:\mathrm{7}{k}\:+\:\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left({k}^{\mathrm{2}} \:+\:\mathrm{2}{k}\:+\:\mathrm{1}\right)\:+\:\mathrm{7}\left({k}\:+\:\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{7}\left({k}+\mathrm{1}\right)\: \\ $$$$\boldsymbol{\mathrm{DONE}}\:! \\ $$$$\mathrm{130520} \\ $$

Commented by Rio Michael last updated on 13/May/20

thanks y′all

$$\mathrm{thanks}\:\mathrm{y}'\mathrm{all} \\ $$

Commented by allizzwell23 last updated on 13/May/20

you′re welcom

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcom} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com