Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93587 by  M±th+et+s last updated on 13/May/20

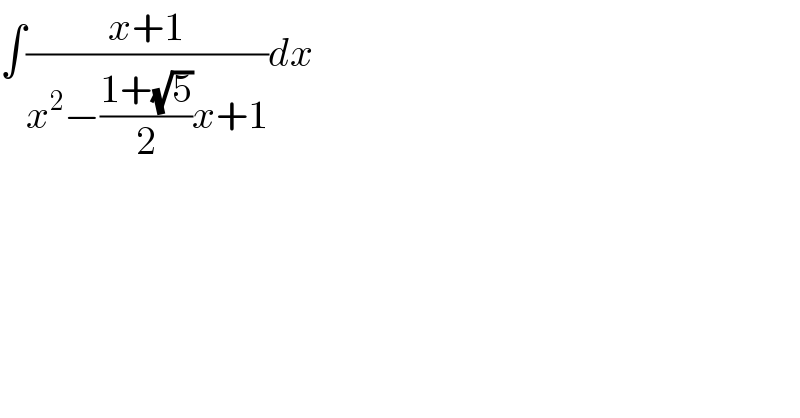
∫((x+1)/(x^2 −((1+(√5))/2)x+1))dx

$$\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}{dx} \\ $$

Answered by niroj last updated on 13/May/20

I= ∫ (( x+1)/(x^2 −((1+(√5))/2)x+1))dx = ∫ (((1/2)(2x−((1+(√5))/2))+ ((5+(√5))/4))/(x^2 −((1+(√5))/2)x+1))dx = (1/2)∫ (( 2x−((1+(√5))/2))/(x^2 −((1+(√5))/2)x+1))dx+ ((5+(√5))/4)∫ (( dx)/(x^2 − ((1+(√5))/2)+1)) = (1/2)log (x^2 −((1+(√5))/2)+1) + ((5+(√5))/4) ∫ (( 1)/((x)^2 −2.x.((1+(√5))/4)+( ((1+(√5))/4))^2 −(((1+(√5))/4))^2 +1))dx +C = (1/2)log (x^2 −((1+(√5))/2)+1)+ ((5+(√5))/4)∫(( 1)/((x−((1+(√5))/4))^2 −{(((1+(√5) )^2 −16)/(16))})) = (1/2)log (x^2 −((1+(√5))/2)+1)+ ((5+(√5))/4)∫ (( 1)/((x−((1+(√5))/4))^2 −((√(( (√5) −5)/8)) )^2 ))dx = (1/2)log (x^2 −((1+(√5))/2)+1)+((5+(√5))/4).(1/(2.(√(( (√5)−5)/8))))log ((x−((1+(√5))/4) −(√(( (√5)−5)/8)))/(x−((1+(√5))/4)+ (√(( (√5) −5)/8)))) +C = (1/2)log (x^2 − ((1+(√5))/2)+1)+((5+(√5))/4).(1/(2((√((√5) −5))/(2(√2)))))log ((((4x−1−(√5))/4) − ((√((√5) −5))/(2(√2))))/(((4x−1−(√5))/4) +((√((√5) −5))/(2(√2))))) +C = (1/2)log (x^2 −((1+(√5))/2)+1)+(((5+(√5) )(√2))/(4(√((√5) −5))))log (((4x−1−(√5) )(√2) −2(√((√5) −5)))/((4x−1−(√5) )(√2) +2(√((√5) −5)))) +C //.

$$\:\:\:\:\mathrm{I}=\:\int\:\frac{\:\:\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+\:\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{2x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx}+\:\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\int\:\frac{\:\:\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)\:+\:\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\:\int\:\frac{\:\:\mathrm{1}}{\left(\mathrm{x}\right)^{\mathrm{2}} −\mathrm{2}.\mathrm{x}.\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}+\left(\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:+\mathrm{C} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)+\:\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\int\frac{\:\:\:\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} −\left\{\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} −\mathrm{16}}{\mathrm{16}}\right\}} \\ $$$$\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)+\:\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\int\:\frac{\:\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\sqrt{\frac{\:\sqrt{\mathrm{5}}\:−\mathrm{5}}{\mathrm{8}}}\:\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)+\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}.\sqrt{\frac{\:\sqrt{\mathrm{5}}−\mathrm{5}}{\mathrm{8}}}}\mathrm{log}\:\frac{\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\:−\sqrt{\frac{\:\:\sqrt{\mathrm{5}}−\mathrm{5}}{\mathrm{8}}}}{\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}+\:\sqrt{\frac{\:\sqrt{\mathrm{5}}\:−\mathrm{5}}{\mathrm{8}}}}\:+\mathrm{C} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)+\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}\frac{\sqrt{\sqrt{\mathrm{5}}\:−\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{2}}}}\mathrm{log}\:\frac{\frac{\mathrm{4x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\:−\:\frac{\sqrt{\sqrt{\mathrm{5}}\:\:−\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\frac{\mathrm{4x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\:+\frac{\sqrt{\sqrt{\mathrm{5}}\:−\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{2}}}}\:+\mathrm{C} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)+\frac{\left(\mathrm{5}+\sqrt{\mathrm{5}}\:\right)\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\sqrt{\mathrm{5}}\:\:−\mathrm{5}}}\mathrm{log}\:\frac{\left(\mathrm{4x}−\mathrm{1}−\sqrt{\mathrm{5}}\:\right)\sqrt{\mathrm{2}}\:−\mathrm{2}\sqrt{\sqrt{\mathrm{5}}\:−\mathrm{5}}}{\left(\mathrm{4x}−\mathrm{1}−\sqrt{\mathrm{5}}\:\right)\sqrt{\mathrm{2}}\:\:+\mathrm{2}\sqrt{\sqrt{\mathrm{5}}\:\:−\mathrm{5}}}\:+\mathrm{C}\://. \\ $$$$\: \\ $$$$\:\: \\ $$$$ \\ $$

Commented by  M±th+et+s last updated on 13/May/20

great work thanx<

$${great}\:{work}\:{thanx}< \\ $$

Commented by niroj last updated on 14/May/20

����

Answered by Ar Brandon last updated on 14/May/20

K=∫((x+1)/(x^2 −((1+(√5))/2)x+1))dx=(1/2)∫((2x−((1+(√5))/2))/(x^2 −((1+(√5))/2)x+1))dx+∫((1+((1+(√5))/4))/(x^2 −((1+(√5))/2)x+1))dx ⇒K=(1/2)ln(x^2 −2xcos36°+1)+∫((1+cos36^° )/((x−cos36^° )^2 +sin^2 36^° ))dx ⇒K=(1/2)ln(x^2 −2xcos36°+1)+((1+cos36^° )/(sin^2 36^° ))∫(1/([((x−cos36^° )/(sin36^° ))]^2 +1))dx ⇒K=(1/2)ln(x^2 −2xcos36°+1)+((1+cos36^° )/(sin36^° ))arctan[((x−cos36^° )/(sin36^° ))]+C

$$\mathrm{K}=\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx}+\int\frac{\mathrm{1}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{cos36}°+\mathrm{1}\right)+\int\frac{\mathrm{1}+\mathrm{cos36}^{°} }{\left({x}−\mathrm{cos36}^{°} \right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \mathrm{36}^{°} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{cos36}°+\mathrm{1}\right)+\frac{\mathrm{1}+\mathrm{cos36}^{°} }{\mathrm{sin}^{\mathrm{2}} \mathrm{36}^{°} }\int\frac{\mathrm{1}}{\left[\frac{{x}−\mathrm{cos36}^{°} }{\mathrm{sin36}^{°} }\right]^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{cos36}°+\mathrm{1}\right)+\frac{\mathrm{1}+\mathrm{cos36}^{°} }{\mathrm{sin36}^{°} }\mathrm{arctan}\left[\frac{{x}−\mathrm{cos36}^{°} }{\mathrm{sin36}^{°} }\right]+\mathrm{C} \\ $$

Commented by  M±th+et+s last updated on 14/May/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by Ar Brandon last updated on 14/May/20

You're welcome ��

Answered by 1549442205 last updated on 14/May/20

F(x)=(1/2)∫(((2x−((1+(√5))/2))+2+((1+(√5))/2) )/(x^2 −((1+(√5))/2)x+1))dx =0.5∫(du/u)+(1+((1+(√5))/(4 )))∫(dx/(x^2 −((1+(√5))/(2 ))x+1)) =0.5ln∣x^2 −((1+(√5))/2)+1∣+((5+(√5))/4)∫((d(x−((1+(√5))/4)))/((x−((1+(√5))/4))^2 +((10−2(√5))/(16)))) =0.5ln∣x^2 −((1+(√5))/2)x+1∣+((5+(√5))/4)×(4/(√(10−2(√5))))tan^(−1) (((x−((1+(√5))/4))/((√(10−2(√5)))/4))) =0.5ln∣x^2 −((1+(√5))/2)x+1∣+((5+(√5))/(√(10−2(√5))))tan^(−1) (((4x−1−(√5))/(√(10−2(√5)))))+C =

$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{2x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+\mathrm{2}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\mathrm{0}.\mathrm{5}\int\frac{\mathrm{du}}{\mathrm{u}}+\left(\mathrm{1}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}\:}\right)\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}\:}\mathrm{x}+\mathrm{1}} \\ $$$$=\mathrm{0}.\mathrm{5ln}\mid\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\mid+\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\int\frac{\mathrm{d}\left(\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)}{\left(\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}} \\ $$$$=\mathrm{0}.\mathrm{5ln}\mid\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}×\frac{\mathrm{4}}{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}}\right) \\ $$$$=\mathrm{0}.\mathrm{5ln}\mid\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\right)+\mathrm{C} \\ $$$$= \\ $$$$ \\ $$

Commented by  M±th+et+s last updated on 14/May/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com