Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93632 by abdomathmax last updated on 14/May/20

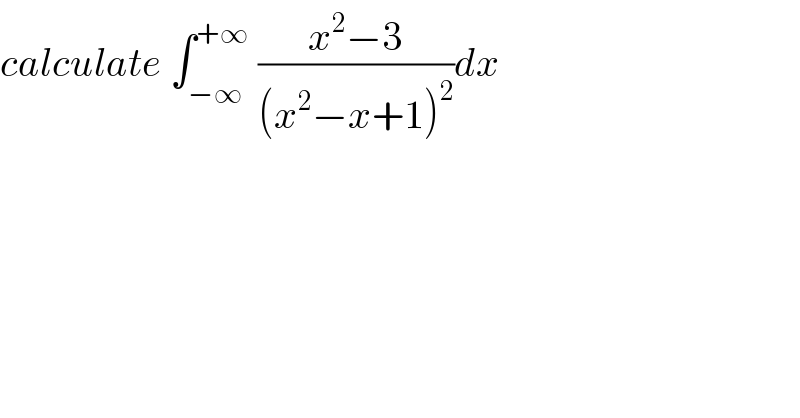
calculate ∫_(−∞) ^(+∞) ((x^2 −3)/((x^2 −x+1)^2 ))dx

$${calculate}\:\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$

Commented by abdomathmax last updated on 15/May/20

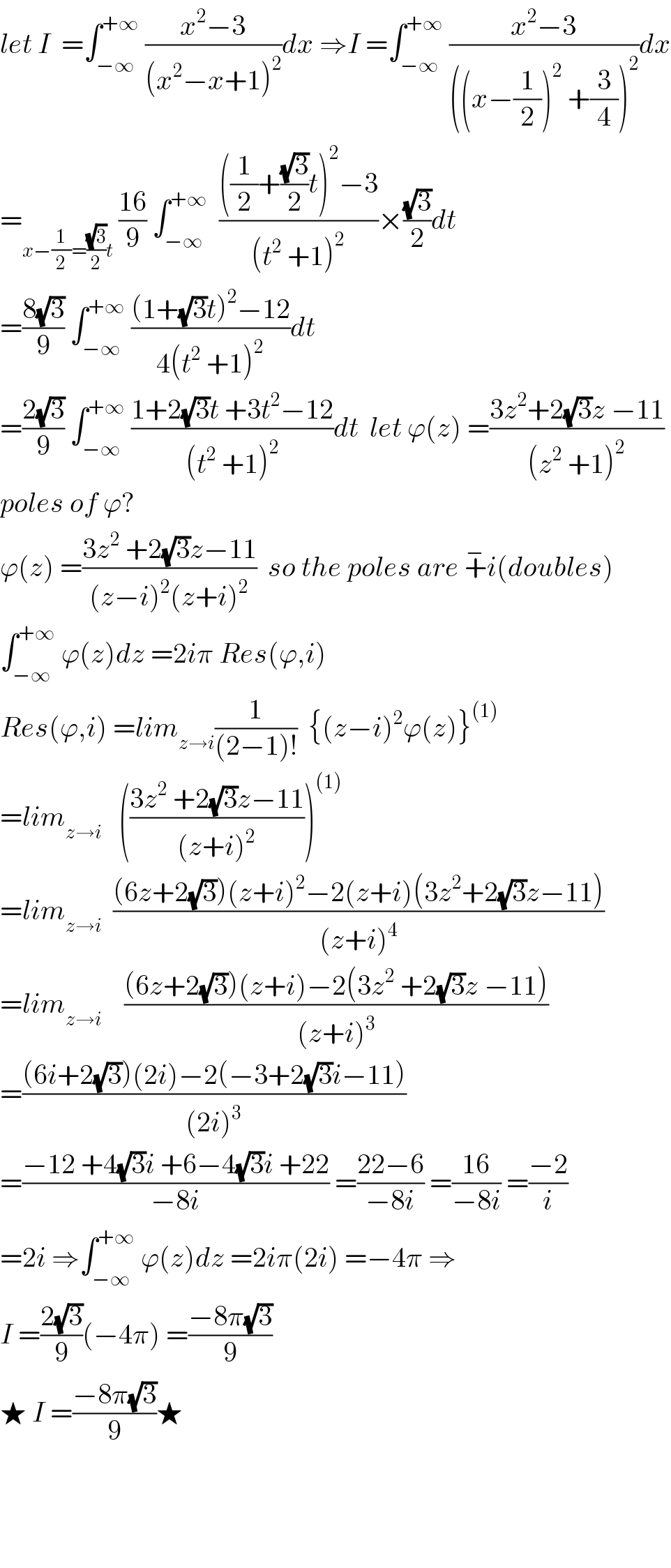
let I =∫_(−∞) ^(+∞) ((x^2 −3)/((x^2 −x+1)^2 ))dx ⇒I =∫_(−∞) ^(+∞) ((x^2 −3)/(((x−(1/2))^2 +(3/4))^2 ))dx =_(x−(1/2)=((√3)/2)t) ((16)/9) ∫_(−∞) ^(+∞) ((((1/2)+((√3)/2)t)^2 −3)/((t^2 +1)^2 ))×((√3)/2)dt =((8(√3))/9) ∫_(−∞) ^(+∞) (((1+(√3)t)^2 −12)/(4(t^2 +1)^2 ))dt =((2(√3))/9) ∫_(−∞) ^(+∞) ((1+2(√3)t +3t^2 −12)/((t^2 +1)^2 ))dt let ϕ(z) =((3z^2 +2(√3)z −11)/((z^2 +1)^2 )) poles of ϕ? ϕ(z) =((3z^2 +2(√3)z−11)/((z−i)^2 (z+i)^2 )) so the poles are +^− i(doubles) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) Res(ϕ,i) =lim_(z→i) (1/((2−1)!)) {(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) (((3z^2 +2(√3)z−11)/((z+i)^2 )))^((1)) =lim_(z→i) (((6z+2(√3))(z+i)^2 −2(z+i)(3z^2 +2(√3)z−11))/((z+i)^4 )) =lim_(z→i) (((6z+2(√3))(z+i)−2(3z^2 +2(√3)z −11))/((z+i)^3 )) =(((6i+2(√3))(2i)−2(−3+2(√3)i−11))/((2i)^3 )) =((−12 +4(√3)i +6−4(√3)i +22)/(−8i)) =((22−6)/(−8i)) =((16)/(−8i)) =((−2)/i) =2i ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ(2i) =−4π ⇒ I =((2(√3))/9)(−4π) =((−8π(√3))/9) ★ I =((−8π(√3))/9)★

$${let}\:{I}\:\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left(\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }{dx} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\frac{\mathrm{16}}{\mathrm{9}}\:\int_{−\infty} ^{+\infty} \:\:\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}\right)^{\mathrm{2}} −\mathrm{3}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int_{−\infty} ^{+\infty} \:\frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}{t}\right)^{\mathrm{2}} −\mathrm{12}}{\mathrm{4}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}{t}\:+\mathrm{3}{t}^{\mathrm{2}} −\mathrm{12}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\:{let}\:\varphi\left({z}\right)\:=\frac{\mathrm{3}{z}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{z}\:−\mathrm{11}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{3}}{z}−\mathrm{11}}{\left({z}−{i}\right)^{\mathrm{2}} \left({z}+{i}\right)^{\mathrm{2}} }\:\:{so}\:{the}\:{poles}\:{are}\:\overset{−} {+}{i}\left({doubles}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{i}\right) \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\:\:\left\{\left({z}−{i}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\:\left(\frac{\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{3}}{z}−\mathrm{11}}{\left({z}+{i}\right)^{\mathrm{2}} }\right)^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\left(\mathrm{6}{z}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({z}+{i}\right)^{\mathrm{2}} −\mathrm{2}\left({z}+{i}\right)\left(\mathrm{3}{z}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{z}−\mathrm{11}\right)}{\left({z}+{i}\right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\:\:\frac{\left(\mathrm{6}{z}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left({z}+{i}\right)−\mathrm{2}\left(\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{3}}{z}\:−\mathrm{11}\right)}{\left({z}+{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{6}{i}+\mathrm{2}\sqrt{\mathrm{3}}\right)\left(\mathrm{2}{i}\right)−\mathrm{2}\left(−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}{i}−\mathrm{11}\right)}{\left(\mathrm{2}{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{12}\:+\mathrm{4}\sqrt{\mathrm{3}}{i}\:+\mathrm{6}−\mathrm{4}\sqrt{\mathrm{3}}{i}\:+\mathrm{22}}{−\mathrm{8}{i}}\:=\frac{\mathrm{22}−\mathrm{6}}{−\mathrm{8}{i}}\:=\frac{\mathrm{16}}{−\mathrm{8}{i}}\:=\frac{−\mathrm{2}}{{i}} \\ $$$$=\mathrm{2}{i}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left(\mathrm{2}{i}\right)\:=−\mathrm{4}\pi\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\left(−\mathrm{4}\pi\right)\:=\frac{−\mathrm{8}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$$\bigstar\:{I}\:=\frac{−\mathrm{8}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\bigstar \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 14/May/20

((x^2 −3)/((x^2 −x+1)))≡((ax+b)/(x^2 −x+1))+((cx+d)/((x^2 −x+1))) =(1/(x^2 −x+1))+((x−4)/((x^2 −x+1)^2 )) ⇒K=∫_(−∞) ^(+∞) ((x^2 −3)/((x^2 −x+1)^2 ))dx=∫_(−∞) ^(+∞) (1/(x^2 −x+1))dx+∫_(−∞) ^(+∞) ((x−4)/((x^2 −x+1)^2 ))dx ⇒K=∫_(−∞) ^(+∞) (1/((x−(1/2))^2 +(3/4)))dx+(1/2)∫_(−∞) ^(+∞) ((2x−1)/((x^2 −x+1)^2 ))dx−(7/2)∫_(−∞) ^(+∞) (1/((x^2 −x+1)^2 ))dx ⇒K=((2(√3))/3)arctan[((2(√3))/3)(x−(1/2))]−(1/(2(x^2 −x+1)))−(7/2)∫_(−∞) ^(+∞) (1/((x^2 −x+1)^2 ))dx J=∫_(−∞) ^(+∞) (1/((x^2 −x+1)^2 ))dx=(1/2)∫_(−∞) ^(+∞) (((x^2 +1)−(x^2 −1))/((x^2 −x+1)^2 ))dx 2J=∫_(−∞) ^(+∞) ((x^2 +1)/((x^2 −x+1)^2 ))dx−∫_(−∞) ^(+∞) ((x^2 −1)/((x^2 −x+1)^2 ))dx ⇒2J=∫_(−∞) ^(+∞) ((x^2 +1)/((x^2 −x+1)^2 ))dx−∫_(−∞) ^(+∞) ((1−(1/x^2 ))/((x−1+(1/x))^2 ))dx ⇒2J=∫_(−∞) ^(+∞) ((x^2 +1)/((x^2 −x+1)^2 ))dx+(x/(x^2 −x+1))

$$\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\equiv\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\frac{\mathrm{cx}+\mathrm{d}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\frac{\mathrm{x}−\mathrm{4}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow\mathrm{K}=\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}+\int_{−\infty} ^{+\infty} \frac{\mathrm{x}−\mathrm{4}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{K}=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{2x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}−\frac{\mathrm{7}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{7}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{J}=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{2J}=\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}−\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2J}=\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}−\int_{−\infty} ^{+\infty} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2J}=\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}+\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$

Answered by Ar Brandon last updated on 14/May/20

((x^2 −3)/((x^2 −x+1)^2 ))≡((ax+b)/(x^2 −x+1))+((cx+d)/((x^2 −x+1)^2 )) =(1/(x^2 −x+1))+((x−4)/((x^2 −x+1)^2 )) ⇒K=∫_(−∞) ^(+∞) ((x^2 −3)/((x^2 −x+1)^2 ))dx=∫_(−∞) ^(+∞) (1/(x^2 −x+1))dx+∫_(−∞) ^(+∞) ((x−4)/((x^2 −x+1)^2 ))dx ⇒K=∫_(−∞) ^(+∞) (1/((x−(1/2))^2 +(3/4)))dx+L ⇒K=((2(√3))/3)[arctan ((2(√3))/3)(x−(1/2))]_(−∞) ^(+∞) +L ⇒K=((2(√3))/3)π+L L_n =∫_(−∞) ^(+∞) ((Ax+B)/((x^2 +px+q)^n ))dx=(A/2)∫_(−∞) ^(+∞) ((2x+p)/((x^2 +px+q)^n ))dx+(B−((Ap)/2))∫_(−∞) ^(+∞) (1/((x^2 +px+q)^n ))dx ⇒L_n =−[(A/(2(n−1)(x^2 +px+q)^(n−1) ))]_(−∞) ^(+∞) +(B−((Ap)/2))∫_(−∞) ^(+∞) (1/([(x+(p/2))^2 +((√(q−(p^2 /4))))^2 ]^n ))dx A=1, B=−4, p=−1, q=1, n=2 ⇒L=−(7/2)∫_(−∞) ^(+∞) (1/([(x−(1/2))^2 +(((√3)/2))^2 ]^2 ))dx J_n =∫_(−∞) ^(+∞) (1/((x^2 +u^2 )^n ))dx ⇒J_(n−1) =∫_(−∞) ^(+∞) (1/((x^2 +u^2 )^(n−1) ))dx=∫_(−∞) ^(+∞) ((x^2 +u^2 )/((x^2 +u^2 )^n ))dx ⇒J_(n−1) =(1/2)∫_(−∞) ^(+∞) x∙((2x)/((x^2 +u^2 )^n ))dx+u^2 J_n ⇒2J_(n−1) =[x∫((2x)/((x^2 +u^2 )^n ))dx]_(−∞) ^(+∞) −∫_(−∞) ^(+∞) ∫((2x)/(x^2 +u^2 ))dxdx+2u^2 J_n ⇒2J_(n−1) =−[(x/((n−1)(x^2 +u^2 )^(n−1) ))]_(−∞) ^(+∞) +(1/(n−1))∫_(−∞) ^(+∞) (1/((x^2 +u^2 )^(n−1) ))dx+2u^2 J_n ⇒2J_(n−1) =(1/(n−1))J_(n−1) +2u^2 J_n ⇒J_n =((2n−3)/(2u^2 (n−1)))J_(n−1) u=((√3)/2), n=2 ⇒−(2/7)L=(2/3)J_1 J_1 =∫_(−∞) ^(+∞) (1/((x−(1/2))^2 +(((√3)/2))^2 ))dx J_1 =((2(√3))/3)[arctan((2(√3))/3)(x−(1/2))]_(−∞) ^(+∞) =((2(√3))/3)π ⇒L=−((14(√3))/9)π ⇒K=((2(√3))/3)π−((14(√3))/9)π ∫_(−∞) ^(+∞) ((x^2 −3)/((x^2 −x+1)^2 ))dx=−((8(√3))/9)π

$$\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }\equiv\frac{\mathrm{a}{x}+\mathrm{b}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{c}{x}+\mathrm{d}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{{x}−\mathrm{4}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{K}=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mathrm{d}{x}+\int_{−\infty} ^{+\infty} \frac{{x}−\mathrm{4}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{K}=\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\mathrm{d}{x}+\mathrm{L} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctan}\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]_{−\infty} ^{+\infty} +\mathrm{L} \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi+\mathrm{L} \\ $$$$\mathrm{L}_{\mathrm{n}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{A}{x}+\mathrm{B}}{\left({x}^{\mathrm{2}} +\mathrm{p}{x}+\mathrm{q}\right)^{\mathrm{n}} }\mathrm{d}{x}=\frac{\mathrm{A}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{x}+\mathrm{p}}{\left({x}^{\mathrm{2}} +\mathrm{p}{x}+\mathrm{q}\right)^{\mathrm{n}} }\mathrm{d}{x}+\left(\mathrm{B}−\frac{\mathrm{Ap}}{\mathrm{2}}\right)\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{p}{x}+\mathrm{q}\right)^{\mathrm{n}} }\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{L}_{\mathrm{n}} =−\left[\frac{\mathrm{A}}{\mathrm{2}\left(\mathrm{n}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{p}{x}+\mathrm{q}\right)^{\mathrm{n}−\mathrm{1}} }\right]_{−\infty} ^{+\infty} +\left(\mathrm{B}−\frac{\mathrm{Ap}}{\mathrm{2}}\right)\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left[\left({x}+\frac{\mathrm{p}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{q}−\frac{\mathrm{p}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} \right]^{\mathrm{n}} }\mathrm{d}{x} \\ $$$$\mathrm{A}=\mathrm{1},\:\mathrm{B}=−\mathrm{4},\:\mathrm{p}=−\mathrm{1},\:\mathrm{q}=\mathrm{1},\:\mathrm{n}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{L}=−\frac{\mathrm{7}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left[\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \right]^{\mathrm{2}} }\mathrm{d}{x} \\ $$$$\mathrm{J}_{\mathrm{n}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}} }\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{J}_{\mathrm{n}−\mathrm{1}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }\mathrm{d}{x}=\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}} }\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{J}_{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} {x}\centerdot\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}} }\mathrm{d}{x}+\mathrm{u}^{\mathrm{2}} \mathrm{J}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{2J}_{\mathrm{n}−\mathrm{1}} =\left[{x}\int\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}} }\mathrm{d}{x}\right]_{−\infty} ^{+\infty} −\int_{−\infty} ^{+\infty} \int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} }\mathrm{d}{x}\mathrm{d}{x}+\mathrm{2u}^{\mathrm{2}} \mathrm{J}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{2J}_{\mathrm{n}−\mathrm{1}} =−\left[\frac{{x}}{\left(\mathrm{n}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }\right]_{−\infty} ^{+\infty} +\frac{\mathrm{1}}{\mathrm{n}−\mathrm{1}}\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }\mathrm{d}{x}+\mathrm{2u}^{\mathrm{2}} \mathrm{J}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{2J}_{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{n}−\mathrm{1}}\mathrm{J}_{\mathrm{n}−\mathrm{1}} +\mathrm{2u}^{\mathrm{2}} \mathrm{J}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{J}_{\mathrm{n}} =\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2u}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}\mathrm{J}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}},\:\mathrm{n}=\mathrm{2} \\ $$$$\Rightarrow−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{L}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{J}_{\mathrm{1}} \\ $$$$\mathrm{J}_{\mathrm{1}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{d}{x} \\ $$$$\mathrm{J}_{\mathrm{1}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctan}\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]_{−\infty} ^{+\infty} =\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi \\ $$$$\Rightarrow\mathrm{L}=−\frac{\mathrm{14}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$$$\Rightarrow\mathrm{K}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi−\frac{\mathrm{14}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$

Commented by mathmax by abdo last updated on 14/May/20

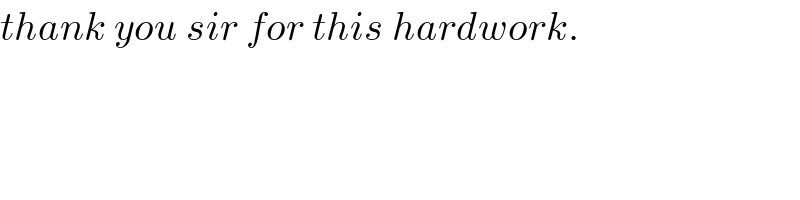
thank you sir for this hardwork.

$${thank}\:{you}\:{sir}\:{for}\:{this}\:{hardwork}. \\ $$

Commented by Ar Brandon last updated on 15/May/20

����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com