
Question and Answers Forum
Question Number 93695 by i jagooll last updated on 14/May/20

Commented by mathmax by abdo last updated on 14/May/20
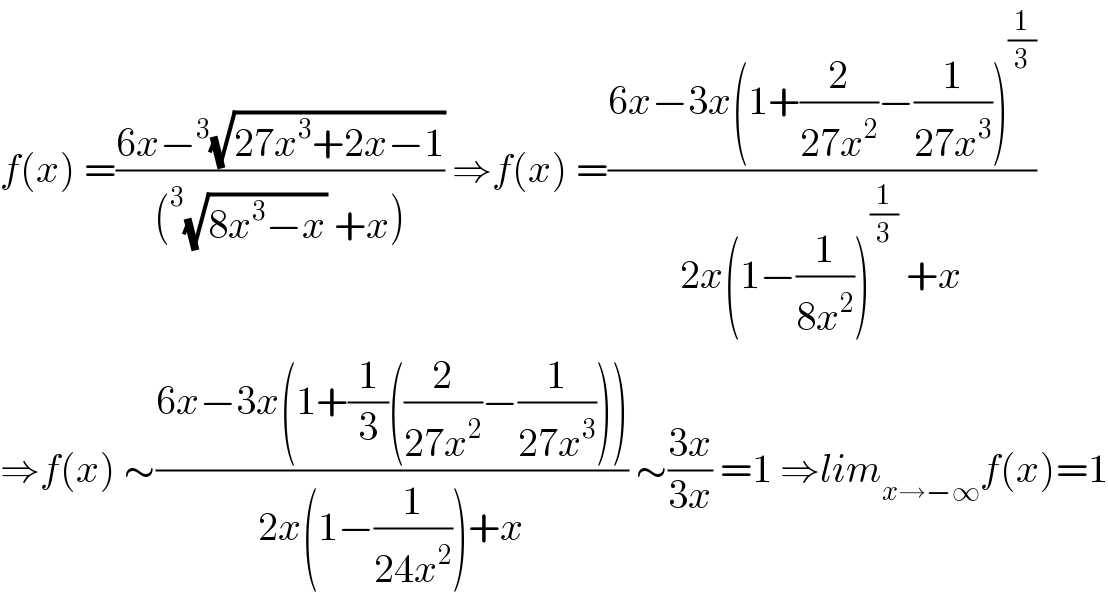
Answered by 1549442205 last updated on 14/May/20
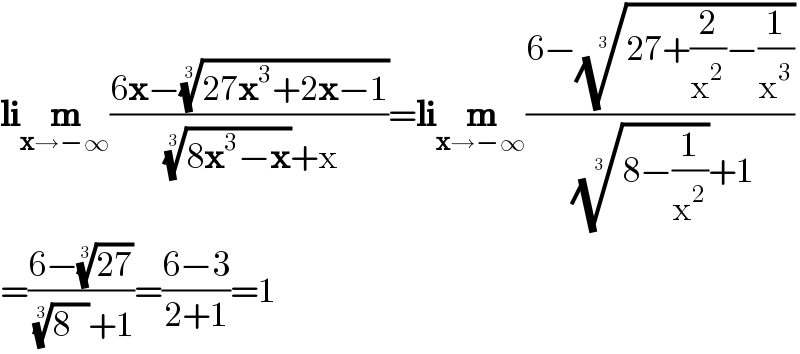
Commented by john santu last updated on 14/May/20

Commented by john santu last updated on 14/May/20

Commented by 1549442205 last updated on 14/May/20

Answered by john santu last updated on 14/May/20
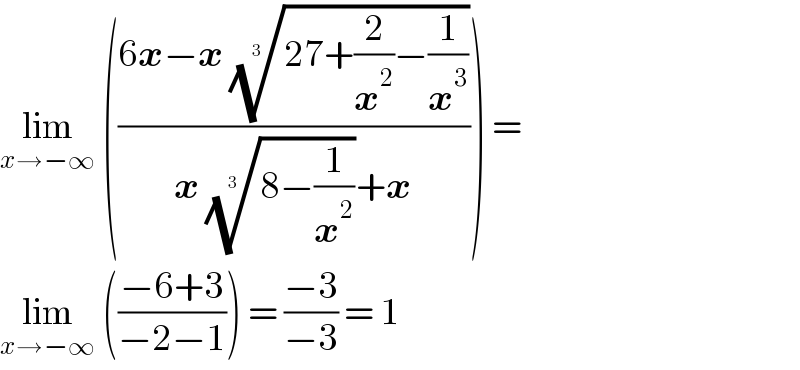
Commented by i jagooll last updated on 14/May/20
cooll man ������
Commented by Ar Brandon last updated on 14/May/20
My man��
