Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 93733 by liki last updated on 14/May/20

Commented by liki last updated on 14/May/20

..please help qn no 6a,b,c

$$..\mathrm{please}\:\mathrm{help}\:\mathrm{qn}\:\mathrm{no}\:\mathrm{6a},\mathrm{b},\mathrm{c} \\ $$

Commented by Rio Michael last updated on 14/May/20

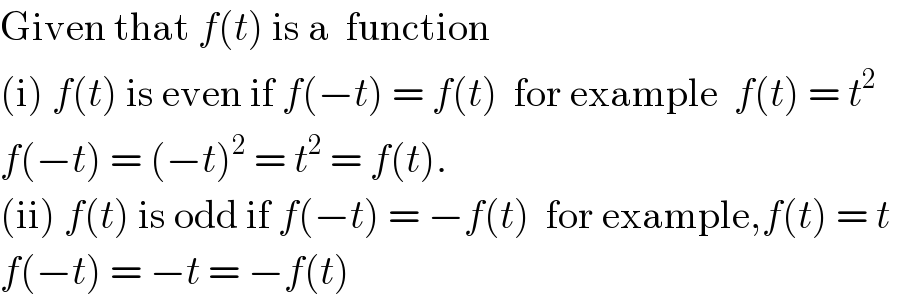
Given that f(t) is a function (i) f(t) is even if f(−t) = f(t) for example f(t) = t^2 f(−t) = (−t)^2 = t^2 = f(t). (ii) f(t) is odd if f(−t) = −f(t) for example,f(t) = t f(−t) = −t = −f(t)

$$\mathrm{Given}\:\mathrm{that}\:{f}\left({t}\right)\:\mathrm{is}\:\mathrm{a}\:\:\mathrm{function}\: \\ $$$$\left(\mathrm{i}\right)\:{f}\left({t}\right)\:\mathrm{is}\:\mathrm{even}\:\mathrm{if}\:{f}\left(−{t}\right)\:=\:{f}\left({t}\right)\:\:\mathrm{for}\:\mathrm{example}\:\:{f}\left({t}\right)\:=\:{t}^{\mathrm{2}} \\ $$$${f}\left(−{t}\right)\:=\:\left(−{t}\right)^{\mathrm{2}} \:=\:{t}^{\mathrm{2}} \:=\:{f}\left({t}\right). \\ $$$$\left(\mathrm{ii}\right)\:{f}\left({t}\right)\:\mathrm{is}\:\mathrm{odd}\:\mathrm{if}\:{f}\left(−{t}\right)\:=\:−{f}\left({t}\right)\:\:\mathrm{for}\:\mathrm{example},{f}\left({t}\right)\:=\:{t}\: \\ $$$${f}\left(−{t}\right)\:=\:−{t}\:=\:−{f}\left({t}\right)\: \\ $$

Commented by Ritu Jain last updated on 14/May/20

hi liki can you please use smaller font size.

$$\mathrm{hi}\:\mathrm{liki} \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{use}\:\mathrm{smaller}\:\mathrm{font}\:\mathrm{size}. \\ $$

Commented by mathmax by abdo last updated on 14/May/20

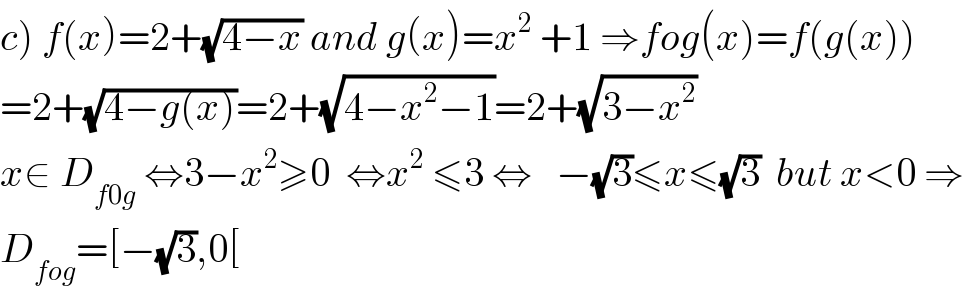
c) f(x)=2+(√(4−x)) and g(x)=x^2 +1 ⇒fog(x)=f(g(x)) =2+(√(4−g(x)))=2+(√(4−x^2 −1))=2+(√(3−x^2 )) x∈ D_(f0g) ⇔3−x^2 ≥0 ⇔x^2 ≤3 ⇔ −(√3)≤x≤(√3) but x<0 ⇒ D_(fog) =[−(√3),0[

$$\left.{c}\right)\:{f}\left({x}\right)=\mathrm{2}+\sqrt{\mathrm{4}−{x}}\:{and}\:{g}\left({x}\right)={x}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow{fog}\left({x}\right)={f}\left({g}\left({x}\right)\right) \\ $$$$=\mathrm{2}+\sqrt{\mathrm{4}−{g}\left({x}\right)}=\mathrm{2}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2}+\sqrt{\mathrm{3}−{x}^{\mathrm{2}} } \\ $$$${x}\in\:{D}_{{f}\mathrm{0}{g}} \:\Leftrightarrow\mathrm{3}−{x}^{\mathrm{2}} \geqslant\mathrm{0}\:\:\Leftrightarrow{x}^{\mathrm{2}} \:\leqslant\mathrm{3}\:\Leftrightarrow\:\:\:−\sqrt{\mathrm{3}}\leqslant{x}\leqslant\sqrt{\mathrm{3}}\:\:{but}\:{x}<\mathrm{0}\:\Rightarrow \\ $$$${D}_{{fog}} =\left[−\sqrt{\mathrm{3}},\mathrm{0}\left[\right.\right. \\ $$

Commented by liki last updated on 14/May/20

..thank you sir i appriciate your time .

$$..\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{appriciate}\:\mathrm{your}\:\mathrm{time}\:. \\ $$

Commented by mathmax by abdo last updated on 14/May/20

8) the line x=3 is dircted by vector v=j(0,1) we have 2y−x =−2 ⇒x−2y =2 ⇒x−2y−2=0 ⇒this line is directed by u(2,1) ⇒(D,Δ) =(u,v) cos(u,v) =((u.v)/(∣∣u∣∣.∣∣v∣∣)) =(1/(√5)) sin(u,v) =((det(u,v))/(∣∣u∣∣.∣∣v∣∣)) =( determinant (((2 0)),((1 1)))/(√5)) =(2/(√5)) ⇒tan(u,v) =2 ⇒ (u,v) =arctan(2)[π]

$$\left.\mathrm{8}\right)\:\:{the}\:{line}\:{x}=\mathrm{3}\:{is}\:{dircted}\:{by}\:{vector}\:{v}={j}\left(\mathrm{0},\mathrm{1}\right)\:\:{we}\:{have} \\ $$$$\mathrm{2}{y}−{x}\:=−\mathrm{2}\:\Rightarrow{x}−\mathrm{2}{y}\:=\mathrm{2}\:\Rightarrow{x}−\mathrm{2}{y}−\mathrm{2}=\mathrm{0}\:\Rightarrow{this}\:{line}\:{is}\:{directed}\:{by} \\ $$$${u}\left(\mathrm{2},\mathrm{1}\right)\:\Rightarrow\left({D},\Delta\right)\:=\left({u},{v}\right)\:\:\:\:{cos}\left({u},{v}\right)\:=\frac{{u}.{v}}{\mid\mid{u}\mid\mid.\mid\mid{v}\mid\mid}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}} \\ $$$${sin}\left({u},{v}\right)\:=\frac{{det}\left({u},{v}\right)}{\mid\mid{u}\mid\mid.\mid\mid{v}\mid\mid}\:=\frac{\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}}{\sqrt{\mathrm{5}}}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\:\Rightarrow{tan}\left({u},{v}\right)\:=\mathrm{2}\:\Rightarrow \\ $$$$\left({u},{v}\right)\:={arctan}\left(\mathrm{2}\right)\left[\pi\right] \\ $$

Commented by abdomathmax last updated on 15/May/20

you are welcome .

$${you}\:{are}\:{welcome}\:. \\ $$

Commented by liki last updated on 15/May/20

..sory sir how can i add more than 256 in whatsap group??

$$..\mathrm{sory}\:\mathrm{sir}\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{add}\:\mathrm{more}\:\mathrm{than}\:\mathrm{256}\:\mathrm{in}\:\mathrm{whatsap}\:\mathrm{group}?? \\ $$

Commented by mathmax by abdo last updated on 15/May/20

A =∫_0 ^π (√(sinx))dx (its not simpson method) A =∫_0 ^(π/2) (√(sinx))dx +∫_(π/2) ^π (√(sinx))dx but ∫_(π/2) ^π (√(sinx))dx =_(x=(π/2)+t) =∫_0 ^(π/2) (√(cost))dt ⇒ A =∫_0 ^(π/2) (√(sinx))dx +∫_0 ^(π/2) (√(cosx))dx =A_1 +A_2 we have x−(x^3 /6)≤sinx ≤x for x∈[0,(π/2)] ⇒ (√(x−(x^3 /6)))≤(√(sinx))≤(√x) ⇒∫_0 ^(π/2) (√(x−(x^3 /6)))dx ≤A_1 ≤∫_0 ^(π/2) (√x)dx but ∫_0 ^(π/2) (√x)dx =_((√x)=t) ∫_0 ^(√(π/2)) t(2t)dt =2[(t^3 /3)]_0 ^(√(π/2)) =(2/3)×(π/2)(√(π/2))= (π/3)(√(π/2)) ∫_0 ^(π/2) (√(x−(x^3 /6)))dx =∫_0 ^(π/2) (√x)(√(1−(x^2 /6)))dx =_((√x)=t) ∫_0 ^(√(π/2)) t(√(1−(t^4 /6)))(2t)dt =2 ∫_0 ^(√(π/2)) t^2 (√(1−(t^4 /6)))dt but we know (1+u)^(1/2) =1+(u/2)+(((1/2)((1/2)−1))/2)u^(2 ) +...=1+(u/2)−(u^2 /8) ⇒ 1+(u/2)−(u^2 /8)≤(√(1+u))≤1+(u/2) ⇒1−(u/2)−(u^2 /8)≤(√(1−u))≤1−(u/2) ⇒1−(t^4 /(12))−(t^8 /(36×8)) ≤(√(1−(t^4 /6)))≤1−(t^4 /(12)) ⇒ t^2 −(t^6 /(12))−(t^(10) /(36×8)) ≤t^2 (√(1−(t^4 /6)))≤t^2 −(t^6 /(12)) ⇒ ∫_0 ^(√(π/2)) (2t^2 −(t^6 /6)−(t^(10) /(144)))dt ≤ ∫_0 ^(π/2) (√(x−(x^3 /6)))dx≤∫_0 ^(√(π/2)) (2t^2 −(t^6 /6))dt ∫_0 ^(√(π/2)) (2t^2 −(t^6 /6))dt =[(2/3)t^3 −(t^7 /(42))]_0 ^(√(π/2)) =(2/3)×(π/2)(√(π/2))−(1/(42))((√(π/2)))^7 ∫_0 ^(√(π/2)) (2t^2 −(t^6 /6)−(t^(10) /(144)))dt =[(2/3)t^3 −(t^7 /(42))−(t^(11) /(11×144))]_0 ^(√(π/2)) ....be continued....

$${A}\:=\int_{\mathrm{0}} ^{\pi} \sqrt{{sinx}}{dx}\:\:\:\left({its}\:{not}\:{simpson}\:{method}\right) \\ $$$${A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\sqrt{{sinx}}{dx}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\sqrt{{sinx}}{dx}\:{but}\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\sqrt{{sinx}}{dx}\:=_{{x}=\frac{\pi}{\mathrm{2}}+{t}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{cost}}{dt}\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\sqrt{{sinx}}{dx}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{cosx}}{dx}\:={A}_{\mathrm{1}} \:+{A}_{\mathrm{2}} \\ $$$${we}\:{have}\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant{sinx}\:\leqslant{x}\:\:{for}\:{x}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:\Rightarrow \\ $$$$\sqrt{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}\leqslant\sqrt{{sinx}}\leqslant\sqrt{{x}}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{dx}\:\leqslant{A}_{\mathrm{1}} \leqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}}{dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}}{dx}\:=_{\sqrt{{x}}={t}} \:\:\:\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\:{t}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}\sqrt{\frac{\pi}{\mathrm{2}}}=\:\frac{\pi}{\mathrm{3}}\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}{dx}\:=_{\sqrt{{x}}={t}} \:\:\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\:{t}\sqrt{\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{6}}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\:\:{t}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{6}}}{dt}\:\:\:{but}\:\:{we}\:{know}\: \\ $$$$\left(\mathrm{1}+{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{{u}}{\mathrm{2}}+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}}{u}^{\mathrm{2}\:} +...=\mathrm{1}+\frac{{u}}{\mathrm{2}}−\frac{{u}^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{1}+\frac{{u}}{\mathrm{2}}−\frac{{u}^{\mathrm{2}} }{\mathrm{8}}\leqslant\sqrt{\mathrm{1}+{u}}\leqslant\mathrm{1}+\frac{{u}}{\mathrm{2}}\:\Rightarrow\mathrm{1}−\frac{{u}}{\mathrm{2}}−\frac{{u}^{\mathrm{2}} }{\mathrm{8}}\leqslant\sqrt{\mathrm{1}−{u}}\leqslant\mathrm{1}−\frac{{u}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{12}}−\frac{{t}^{\mathrm{8}} }{\mathrm{36}×\mathrm{8}}\:\leqslant\sqrt{\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{6}}}\leqslant\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{12}}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} −\frac{{t}^{\mathrm{6}} }{\mathrm{12}}−\frac{{t}^{\mathrm{10}} }{\mathrm{36}×\mathrm{8}}\:\leqslant{t}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{t}^{\mathrm{4}} }{\mathrm{6}}}\leqslant{t}^{\mathrm{2}} \:−\frac{{t}^{\mathrm{6}} }{\mathrm{12}}\:\Rightarrow\: \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\:\left(\mathrm{2}{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{6}} }{\mathrm{6}}−\frac{{t}^{\mathrm{10}} }{\mathrm{144}}\right){dt}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{dx}\leqslant\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\:\left(\mathrm{2}{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{6}} }{\mathrm{6}}\right){dt} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\left(\mathrm{2}{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{6}} }{\mathrm{6}}\right){dt}\:=\left[\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} −\frac{{t}^{\mathrm{7}} }{\mathrm{42}}\right]_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}\sqrt{\frac{\pi}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{42}}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right)^{\mathrm{7}} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \:\:\left(\mathrm{2}{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{6}} }{\mathrm{6}}−\frac{{t}^{\mathrm{10}} }{\mathrm{144}}\right){dt}\:=\left[\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} −\frac{{t}^{\mathrm{7}} }{\mathrm{42}}−\frac{{t}^{\mathrm{11}} }{\mathrm{11}×\mathrm{144}}\right]_{\mathrm{0}} ^{\sqrt{\frac{\pi}{\mathrm{2}}}} \\ $$$$....{be}\:{continued}.... \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 15/May/20

I =∫_0 ^π (√(sinx))dx let use simpson method ∫_a ^b f(x)dx ∼ ((b−a)/6){ f(a) +f(((a+b)/2))+f(b)} with f(x)=(√(sinx))we get ∫_0 ^π (√(sinx))dx ∼(π/6){ (√(sin0)) +(√(sin((π/2)))) +(√(sinπ))} ⇒∫_0 ^π (√(sinx))dx ∼(π/6)

$${I}\:=\int_{\mathrm{0}} ^{\pi} \sqrt{{sinx}}{dx}\:\:{let}\:{use}\:{simpson}\:{method}\: \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:\sim\:\frac{{b}−{a}}{\mathrm{6}}\left\{\:{f}\left({a}\right)\:+{f}\left(\frac{{a}+{b}}{\mathrm{2}}\right)+{f}\left({b}\right)\right\}\:\:{with}\:{f}\left({x}\right)=\sqrt{{sinx}}{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\pi} \sqrt{{sinx}}{dx}\:\sim\frac{\pi}{\mathrm{6}}\left\{\:\sqrt{{sin}\mathrm{0}}\:\:+\sqrt{{sin}\left(\frac{\pi}{\mathrm{2}}\right)}\:+\sqrt{{sin}\pi}\right\} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \:\sqrt{{sinx}}{dx}\:\sim\frac{\pi}{\mathrm{6}} \\ $$

Answered by Rio Michael last updated on 14/May/20

6.(b) f(x) = (x−2)(8−x) for 2 ≤ x≤ 8 (i) f(−1) = (−1−2)(8+1) = −27 (ii) f(1−2t) = (1−2t−2)(8−1 +2t) = (−1−2t)(9−2t) D_f : t ∈R

$$\mathrm{6}.\left(\mathrm{b}\right)\:{f}\left({x}\right)\:=\:\left({x}−\mathrm{2}\right)\left(\mathrm{8}−{x}\right)\:\mathrm{for}\:\mathrm{2}\:\leqslant\:{x}\leqslant\:\mathrm{8}\: \\ $$$$\left(\mathrm{i}\right)\:{f}\left(−\mathrm{1}\right)\:=\:\left(−\mathrm{1}−\mathrm{2}\right)\left(\mathrm{8}+\mathrm{1}\right)\:=\:−\mathrm{27} \\ $$$$\left(\mathrm{ii}\right)\:{f}\left(\mathrm{1}−\mathrm{2}{t}\right)\:=\:\left(\mathrm{1}−\mathrm{2}{t}−\mathrm{2}\right)\left(\mathrm{8}−\mathrm{1}\:+\mathrm{2}{t}\right)\:=\:\left(−\mathrm{1}−\mathrm{2}{t}\right)\left(\mathrm{9}−\mathrm{2}{t}\right)\:\:\mathrm{D}_{{f}} \::\:{t}\:\in\mathbb{R} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 15/May/20

The function is defined in interval 2 ≤ x≤ 8. How can you calculate f(−1)? ∴ f(−1) is undefined!

$$\mathcal{T}{he}\:{function}\:{is}\:{defined}\:{in}\:{interval} \\ $$$$\mathrm{2}\:\leqslant\:{x}\leqslant\:\mathrm{8}.\:\mathcal{H}{ow}\:{can}\:{you}\:{calculate} \\ $$$${f}\left(−\mathrm{1}\right)? \\ $$$$\therefore\:{f}\left(−\mathrm{1}\right)\:{is}\:{undefined}! \\ $$

Answered by Rio Michael last updated on 14/May/20

f(t) = (t/2)(((e^t +1)/(e^t −1))) f(−t) = ((−t)/2)(((e^(−t) +1)/(e^(−t) −1))) = −(t/2)(((1 + e^t )/(1−e^t ))) = (t/2)(((e^t +1)/(e^t −1))) hencef(t) is even as f(−t) = f(t)

$${f}\left({t}\right)\:=\:\frac{{t}}{\mathrm{2}}\left(\frac{{e}^{{t}} +\mathrm{1}}{{e}^{{t}} −\mathrm{1}}\right) \\ $$$${f}\left(−{t}\right)\:=\:\frac{−{t}}{\mathrm{2}}\left(\frac{{e}^{−{t}} +\mathrm{1}}{{e}^{−{t}} −\mathrm{1}}\right)\:\:=\:−\frac{{t}}{\mathrm{2}}\left(\frac{\mathrm{1}\:+\:{e}^{{t}} }{\mathrm{1}−{e}^{{t}} }\right)\:=\:\frac{{t}}{\mathrm{2}}\left(\frac{{e}^{{t}} +\mathrm{1}}{{e}^{{t}} −\mathrm{1}}\right) \\ $$$$\mathrm{hence}{f}\left({t}\right)\:\mathrm{is}\:\mathrm{even}\:\mathrm{as}\:{f}\left(−{t}\right)\:=\:{f}\left({t}\right) \\ $$

Answered by Rio Michael last updated on 14/May/20

6(c) f(x) = 2+ (√(4−x)) and g(x) = x^2 +1 f o g = f[g(x)] = f(x^2 +1) = 2+ (√(4−x^2 −1)) = 2 + (√(3−x^2 )) D_(fg) : x∈R −{−(√3),(√3)} as an exercise find the range of your function

$$\mathrm{6}\left(\mathrm{c}\right)\:{f}\left({x}\right)\:=\:\mathrm{2}+\:\sqrt{\mathrm{4}−{x}}\:\mathrm{and}\:\mathrm{g}\left({x}\right)\:=\:{x}^{\mathrm{2}} \:+\mathrm{1} \\ $$$${f}\:{o}\:{g}\:=\:{f}\left[\mathrm{g}\left({x}\right)\right]\:=\:{f}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:=\:\mathrm{2}+\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\mathrm{2}\:+\:\sqrt{\mathrm{3}−{x}^{\mathrm{2}} }\:\mathrm{D}_{{fg}} \::\:\:{x}\in\mathbb{R}\:−\left\{−\sqrt{\mathrm{3}},\sqrt{\mathrm{3}}\right\} \\ $$$$\mathrm{as}\:\mathrm{an}\:\mathrm{exercise}\:\mathrm{find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{your}\:\mathrm{function} \\ $$

Commented by liki last updated on 14/May/20

..Thank you very much sir.

$$..\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 14/May/20

you are requested to use a smaller font for your text sir!

$${you}\:{are}\:{requested}\:{to}\:{use}\:{a}\:{smaller} \\ $$$${font}\:{for}\:{your}\:{text}\:{sir}! \\ $$

Commented by Tinku Tara last updated on 14/May/20

Another request is to please crop image so that only useful portion is posted. Latest verion provides crop function which uploading images.

$$\mathrm{Another}\:\mathrm{request}\:\mathrm{is}\:\mathrm{to}\:\mathrm{please}\:\mathrm{crop} \\ $$$$\mathrm{image}\:\mathrm{so}\:\mathrm{that}\:\mathrm{only}\:\mathrm{useful}\:\mathrm{portion} \\ $$$$\mathrm{is}\:\mathrm{posted}.\:\mathrm{Latest}\:\mathrm{verion}\:\mathrm{provides} \\ $$$$\mathrm{crop}\:\mathrm{function}\:\mathrm{which}\:\mathrm{uploading} \\ $$$$\mathrm{images}. \\ $$

Commented by Ar Brandon last updated on 14/May/20

OK Sir��

Commented by liki last updated on 15/May/20

..ok sir

$$..\mathrm{ok}\:\mathrm{sir} \\ $$

Answered by Rasheed.Sindhi last updated on 14/May/20

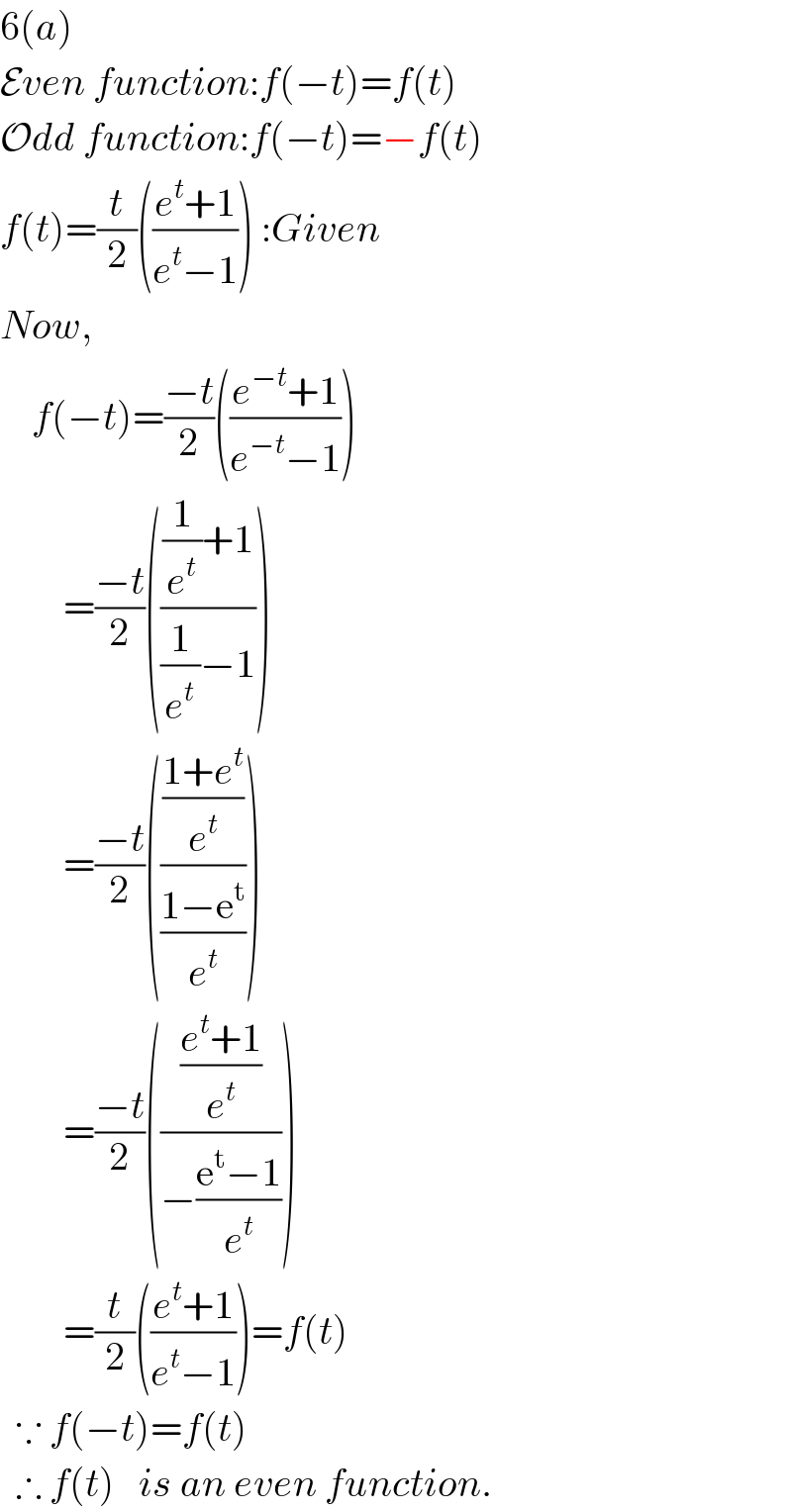
6(a) Even function:f(−t)=f(t) Odd function:f(−t)=−f(t) f(t)=(t/2)(((e^t +1)/(e^t −1))) :Given Now, f(−t)=((−t)/2)(((e^(−t) +1)/(e^(−t) −1))) =((−t)/2)((((1/e^t )+1)/((1/e^t )−1))) =((−t)/2)((((1+e^t )/e^t )/((1−e^t )/e^t ))) =((−t)/2)((((e^t +1)/e^t )/(−((e^t −1)/e^t )))) =(t/2)(((e^t +1)/(e^t −1)))=f(t) ∵ f(−t)=f(t) ∴ f(t) is an even function.

$$\mathrm{6}\left({a}\right) \\ $$$$\mathcal{E}{ven}\:{function}:{f}\left(−{t}\right)={f}\left({t}\right) \\ $$$$\mathcal{O}{dd}\:{function}:{f}\left(−{t}\right)=−{f}\left({t}\right) \\ $$$${f}\left({t}\right)=\frac{{t}}{\mathrm{2}}\left(\frac{{e}^{{t}} +\mathrm{1}}{{e}^{{t}} −\mathrm{1}}\right)\::{Given} \\ $$$${Now}, \\ $$$$\:\:\:\:{f}\left(−{t}\right)=\frac{−{t}}{\mathrm{2}}\left(\frac{{e}^{−{t}} +\mathrm{1}}{{e}^{−{t}} −\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{−{t}}{\mathrm{2}}\left(\frac{\frac{\mathrm{1}}{{e}^{{t}} }+\mathrm{1}}{\frac{\mathrm{1}}{{e}^{{t}} }−\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{−{t}}{\mathrm{2}}\left(\frac{\frac{\mathrm{1}+{e}^{{t}} }{{e}^{{t}} }}{\frac{\mathrm{1}−\mathrm{e}^{\mathrm{t}} }{{e}^{{t}} }}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{−{t}}{\mathrm{2}}\left(\frac{\frac{{e}^{{t}} +\mathrm{1}}{{e}^{{t}} }}{−\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{1}}{{e}^{{t}} }}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{{t}}{\mathrm{2}}\left(\frac{{e}^{{t}} +\mathrm{1}}{{e}^{{t}} −\mathrm{1}}\right)={f}\left({t}\right) \\ $$$$\:\:\because\:{f}\left(−{t}\right)={f}\left({t}\right) \\ $$$$\:\:\therefore\:{f}\left({t}\right)\:\:\:{is}\:{an}\:{even}\:{function}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com