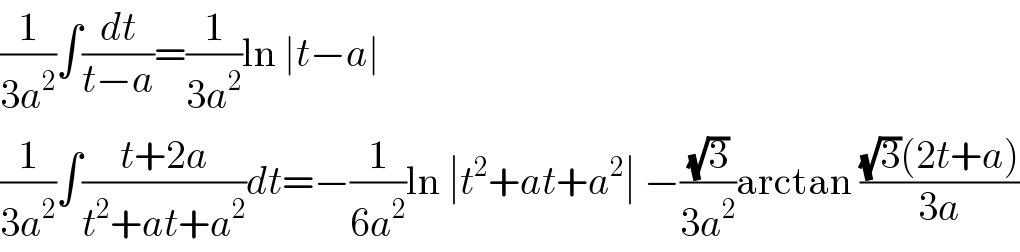Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93804 by i jagooll last updated on 15/May/20

$$\int x\sqrt[3]{\frac{3x-1}{x+2}}dx?$$

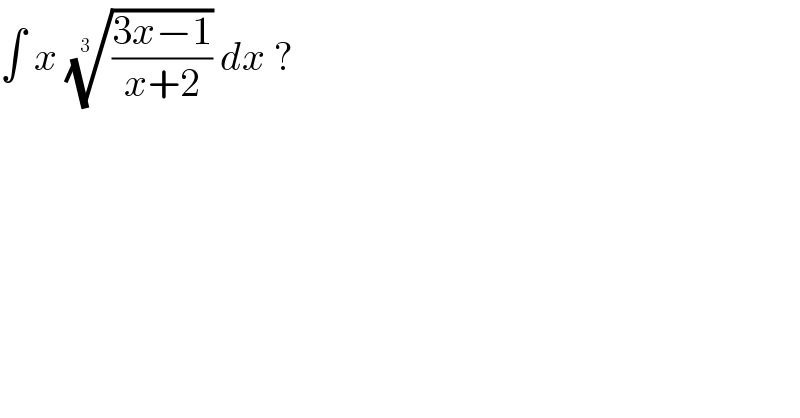
Commented by i jagooll last updated on 15/May/20

$$\mathrm{set}{\mathrm{t}}^3=\frac{3\mathrm{x}-1}{\mathrm{x}+2}\Rightarrow {\mathrm{xt}}^3+{2\mathrm{t}}^3=3\mathrm{x}-1$$$$\mathrm{x}=\frac{-1-{2\mathrm{t}}^3}{{\mathrm{t}}^3-3}=\frac{-{2\mathrm{t}}^3-1}{{\mathrm{t}}^3-1}$$$$\mathrm{dx}=\frac{{9\mathrm{t}}^2}{{({\mathrm{t}}^3-1)}^2}\mathrm{dt}$$$$\Rightarrow \int \left(\frac{-{2\mathrm{t}}^3-1}{{\mathrm{t}}^3-3}\right).\mathrm{t}\left(\frac{{9\mathrm{t}}^2}{{({\mathrm{t}}^3-1)}^2}\right)\mathrm{dt}$$$$\int \frac{-{9\mathrm{t}}^3({2\mathrm{t}}^3+1)}{{({\mathrm{t}}^3-1)}^2({\mathrm{t}}^3-3)}\mathrm{dt}$$$$\mathrm{stuck}???$$

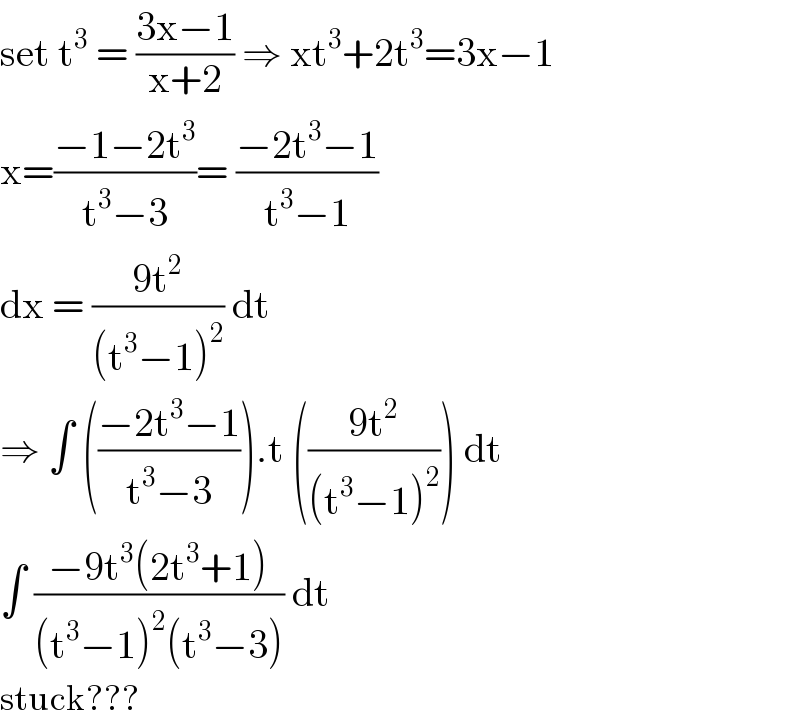
Commented by mathmax by abdo last updated on 15/May/20

$$thisintegralissolvedbyalotsofcalculus$$$$I=\int x\left({}^3\sqrt{\frac{3x-1}{x+2}}\right)dxchangement{}^3\sqrt{\frac{3x-1}{x+2}}=tgive$$$$\frac{3x-1}{x+2}=t^3\Rightarrow 3x-1=t^{3}x+2t^3\Rightarrow (3-t^3)x=2t^3+1\Rightarrow x=\frac{2t^3+1}{3-t^3}$$$$\Rightarrow \frac{dx}{dt}=\frac{6t^2(3-t^3)-(2t^3+1)(-3t^2)}{{(3-t^3)}^2}=\frac{18t^2-6t^5+6t^5-3t^2}{{(3-t^3)}^2}$$$$=\frac{15t^2}{{(3-t^3)}^2}\Rightarrow I=\int \left(\frac{2t^3+1}{3-t^3}\right)t\frac{15t^2}{{(3-t^3)}^2}dt$$$$=\int \frac{30t^5+15t^2}{{(3-t^3)}^3}dt=-15\int \frac{2t^5+t^2}{{(t^3-3)}^3}dtlet\alpha {=}^3\sqrt{3}\Rightarrow$$$$\int \frac{2t^5+t^2}{{(t^3-{\alpha }^3)}^3}dt=\int \frac{2t^5+t^2}{{(t-\alpha )}^3{(t^2+\alpha t+{\alpha }^2)}^3}dt$$$$=\int \frac{2t^5+t^2}{{\left(\frac{t-\alpha }{t^2+\alpha t+{\alpha }^2}\right)}^3{(t^2+\alpha t+{\alpha }^2)}^6}dtchangement\frac{t-\alpha }{t^2+\alpha t+{\alpha }^2}=ugive$$$$t+\alpha ={ut}^2+u\alpha t+u{\alpha }^2\Rightarrow {ut}^2+u\alpha t-t-\alpha +u{\alpha }^2=0\Rightarrow$$$${ut}^2+(\alpha u-1)t+u{\alpha }^2-\alpha =0$$$$\mathrm{\Delta }={(\alpha u-1)}^2-4u(u{\alpha }^2-\alpha )={\alpha }^2{u}^2-2\alpha u-4{\alpha }^2{u}^2+4\alpha u$$$$=-3{\alpha }^2{u}^2+2\alpha u\Rightarrow t=\frac{1-\alpha u\stackrel{-}{+}\sqrt{2\alpha u-3{\alpha }^2{u}^2}}{2u}\Rightarrow$$$$t=\frac{1}{2u}-\frac{\alpha }{2}\stackrel{-}{+}\frac{\sqrt{2\alpha u-3{\alpha }^2{u}^2}}{2u}\Rightarrow$$$$\frac{dt}{du}=-\frac{1}{2u^2}\stackrel{-}{+}\frac{1}{2}{\left(\sqrt{\frac{2\alpha u}{4u^2}-\frac{3{\alpha }^2{u}^2}{4u^2}}\right)}^{{}^{\prime }}$$$$=-\frac{1}{2u^2}\stackrel{-}{+}\frac{1}{2}{\left(\sqrt{\frac{\alpha }{2u}-\frac{3{\alpha }^2}{4}}\right)}^{{}^{\prime }}=-\frac{1}{2u^2}\stackrel{-}{+}\frac{1}{2}\left(\frac{-\frac{\alpha }{2u^2}}{2\sqrt{\frac{\alpha }{2u}-\frac{3{\alpha }^2}{4}}}\right)$$$$=-\frac{1}{2u^2}\stackrel{-}{+}\frac{\alpha }{8u^2\sqrt{\frac{\alpha }{2u}-\frac{3{\alpha }^2}{4}}}....becontinued....$$$$$$

Commented by i jagooll last updated on 15/May/20

$$\mathrm{very}\mathrm{hard}\mathrm{sir}?$$

Answered by MJS last updated on 15/May/20

$$\int x\sqrt[3]{\frac{3x-1}{x+2}}dx=$$$$[t=\sqrt[3]{\frac{3x-1}{x+2}}\iff x=-\frac{2t^3+1}{t^3-3}\to dx=\frac{21t^2}{{(t^3-3)}^2}dt]$$$$=-21\int \frac{t^3(2t^3+1)}{{(t^3-3)}^3}dt=$$$$\left[\mathrm{Ostrogradski}\right]$$$$=\frac{7t(43t^3-66)}{18{(t^3-3)}^2}-\frac{77}{9}\int \frac{dt}{t^3-3}$$$$\mathrm{now}\mathrm{use}\mathrm{this}\mathrm{formula}:$$$$\int \frac{dt}{t^3-a^3}=\frac{1}{3a^2}\int \frac{dt}{t-a}-\frac{1}{3a^2}\int \frac{t+2a}{t^2+at+a^2}dt$$$$\mathrm{these}\mathrm{should}\mathrm{be}\mathrm{easy}\mathrm{to}\mathrm{solve}$$

Commented by MJS last updated on 15/May/20

$$\frac{1}{3a^2}\int \frac{dt}{t-a}=\frac{1}{3a^2}\ln \mid t-a\mid$$$$\frac{1}{3a^2}\int \frac{t+2a}{t^2+at+a^2}dt=-\frac{1}{6a^2}\ln \mid t^2+at+a^2\mid -\frac{\sqrt{3}}{3a^2}\arctan \frac{\sqrt{3}(2t+a)}{3a}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com