
Question and Answers Forum
Question Number 93859 by M±th+et+s last updated on 15/May/20
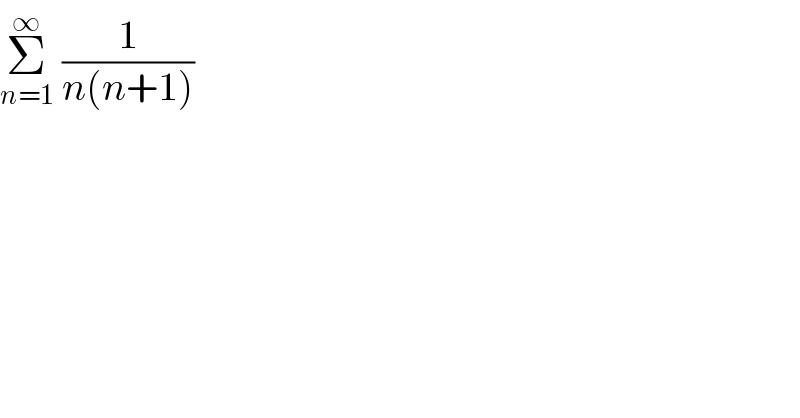
Answered by Ar Brandon last updated on 15/May/20
![(1/(n(n+1)))=(1/n)−(1/(n+1))⇒Σ_(n=1) ^∞ (1/(n(n+1)))=Σ_(n=1) ^∞ [(1/n)−(1/(n+1))]=lim_(k→+∞) Σ_(n=1) ^k [(1/n)−(1/(n+1))] =lim_(k→+∞) [1−(1/2)+(1/2)−(1/3)+(1/3)−(1/4)+∙∙∙+(1/k)−(1/(k+1))] =lim_(k→+∞) [1−(1/(k+1))]=1](Q93861.png)
| ||
Question and Answers Forum | ||
Question Number 93859 by M±th+et+s last updated on 15/May/20 | ||
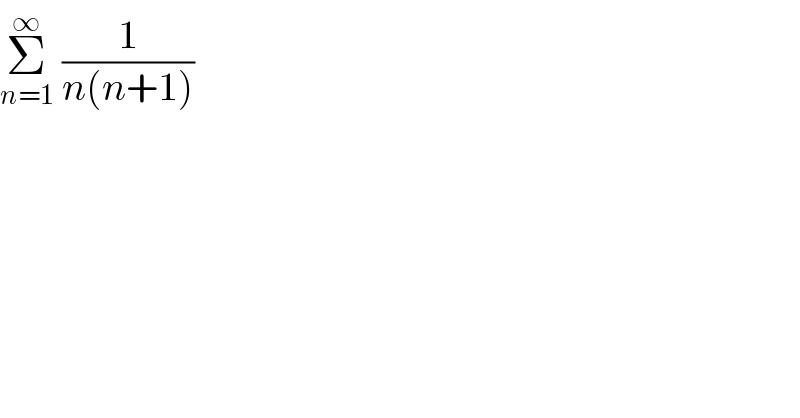 | ||
Answered by Ar Brandon last updated on 15/May/20 | ||
![(1/(n(n+1)))=(1/n)−(1/(n+1))⇒Σ_(n=1) ^∞ (1/(n(n+1)))=Σ_(n=1) ^∞ [(1/n)−(1/(n+1))]=lim_(k→+∞) Σ_(n=1) ^k [(1/n)−(1/(n+1))] =lim_(k→+∞) [1−(1/2)+(1/2)−(1/3)+(1/3)−(1/4)+∙∙∙+(1/k)−(1/(k+1))] =lim_(k→+∞) [1−(1/(k+1))]=1](Q93861.png) | ||
| ||