Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93937 by seedhamaieng@gmail.com last updated on 16/May/20

$$\int \frac{1}{\sqrt{\tan x}}dx=?$$

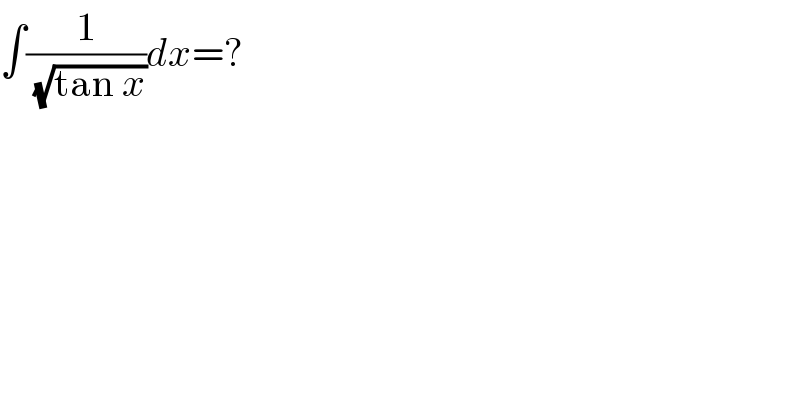
Commented by i jagooll last updated on 16/May/20

$$\int \frac{\sec {}^2\mathrm{x}}{\sec {}^2\mathrm{x}\sqrt{\tan \mathrm{x}}}\mathrm{dx}=$$$$\int \frac{\mathrm{du}}{(1+{\mathrm{u}}^2)\sqrt{\mathrm{u}}},[\mathrm{u}=\tan \mathrm{x}]$$$$$$

Commented by seedhamaieng@gmail.com last updated on 16/May/20

thanks

Commented by prakash jain last updated on 16/May/20

$$\sqrt{\tan x}=u$$$$\tan x=u^2$$$${\sec }^{2}xdx=2udu$$$$(1+{\tan }^{2}x)dx=2udu$$$$(1+u^4)dx=2udu$$$$dx=\frac{2udu}{(1+u^4)}$$$$\mathrm{substituting}\mathrm{value}\mathrm{of}x\mathrm{and}\mathrm{d}x\mathrm{in}\mathrm{integral}$$$$\int \frac{1}{u}\times \frac{2u}{(1+u^4)}du$$$$=\int \frac{2}{1+u^4}du$$$$=\int \frac{u^2+1+1-u^2}{1+u^4}du$$$$=\int \frac{u^2+1}{1+u^4}du-\int \frac{u^2-1}{1+u^4}du$$$$=\int \frac{1+\frac{1}{u^2}}{u^2+\frac{1}{u^2}-2+2}du-\int \frac{1-\frac{1}{u^2}}{u^2+\frac{1}{u^2}+2-2}du$$$$=\int \frac{1+\frac{1}{u^2}}{{(u-\frac{1}{u})}^2+2}du-\int \frac{1-\frac{1}{u^2}}{{(u+\frac{1}{u})}^2-2}du$$$$infirstintegrlv=u-\frac{1}{u}$$$$insecondintegrlv=u+\frac{1}{u}$$$$=\int \frac{dv}{v^2+2}+\int \frac{dv}{v^2-2}$$$$\mathrm{Now}\mathrm{the}\mathrm{integral}\mathrm{can}\mathrm{be}\mathrm{solved}$$$$\mathrm{using}\mathrm{formulas}\mathrm{for}$$$$\frac{1}{x^2+a^2},\frac{1}{x^2-a^2}$$$$\mathrm{subtitute}v\mathrm{with}u\mathrm{and}\mathrm{then}x\mathrm{to}$$$$\mathrm{g}o\mathrm{et}\mathrm{final}\mathrm{answer}$$

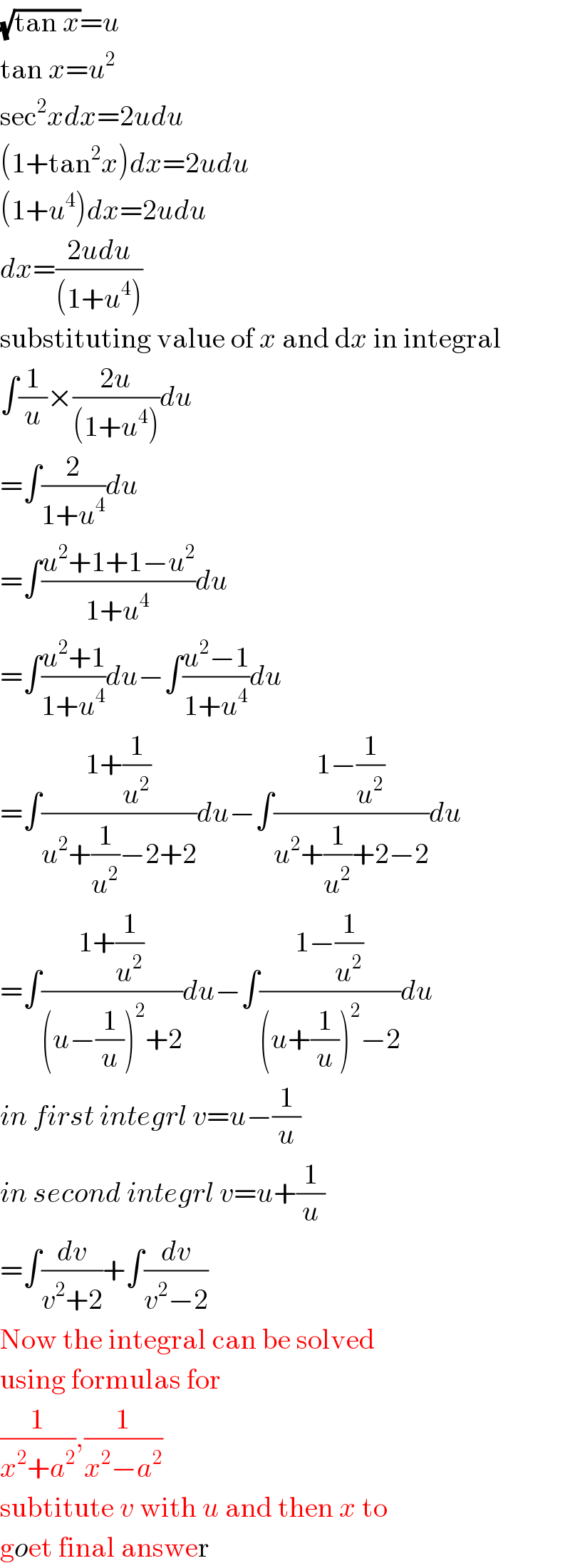
Commented by seedhamaieng@gmail.com last updated on 16/May/20

thanks sir

Commented by mathmax by abdo last updated on 16/May/20

$$I=\int \frac{dx}{\sqrt{tanx}}changement\sqrt{tanx}=tgivetanx=t^2\Rightarrow x=arctan\left(t^2\right)$$$$I=\int \frac{2t}{(1+t^4)t}dt=\int \frac{2dt}{1+t^4}=\int \frac{\frac{2}{t^2}}{\frac{1}{t^2}+t^2}dt$$$$=\int \frac{1+\frac{1}{t^2}+1-\frac{1}{t^2}}{t^2+\frac{1}{t^2}}dt=\int \frac{1+\frac{1}{t^2}}{{(t-\frac{1}{t})}^2+2}dt+\int \frac{1-\frac{1}{t^2}}{{(t+\frac{1}{t})}^2-2}dt=I_1+I_2$$$$I_1{=}_{t-\frac{1}{t}=u}\int \frac{du}{u^2+2}{=}_{u=\sqrt{2}z}\int \frac{\sqrt{2}dz}{2(1+z^2)}=\frac{1}{\sqrt{2}}arctan\left(\frac{u}{\sqrt{2}}\right)+c_1$$$$=\frac{1}{\sqrt{2}}arctan\left(\frac{1}{\sqrt{2}}(t-\frac{1}{t})\right)+c_1=\frac{1}{\sqrt{2}}arctan\left(\frac{1}{\sqrt{2}}(\sqrt{tanx}-\frac{1}{\sqrt{tanx}})\right)+c_1$$$$I_2{=}_{t+\frac{1}{t}=z}\int \frac{dz}{z^2-2}=\int \frac{dz}{(z-\sqrt{2})(z+\sqrt{2})}=\frac{1}{2\sqrt{2}}\int (\frac{1}{z-\sqrt{2}}-\frac{1}{z+\sqrt{2}})dz$$$$=\frac{1}{2\sqrt{2}}ln\mid \frac{z-\sqrt{2}}{z+\sqrt{2}}\mid +c_2=\frac{1}{2\sqrt{2}}ln\mid \frac{\sqrt{tanx}+\frac{1}{\sqrt{tanx}}-\sqrt{2}}{\sqrt{tanx}+\frac{1}{\sqrt{tanx}}+\sqrt{2}}\mid +c_2$$$$andI=I_1+I_2$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com