Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93941 by Ar Brandon last updated on 16/May/20

Show that the function f(x)=e^(x ) is of Reimann within x∈[1;5] hence calculate ∫_1 ^5 e^x dx

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{x}\:} \:\mathrm{is}\:\mathrm{of}\:\mathrm{Reimann}\:\mathrm{within} \\ $$$$\mathrm{x}\in\left[\mathrm{1};\mathrm{5}\right]\:\mathrm{hence}\:\mathrm{calculate}\:\int_{\mathrm{1}} ^{\mathrm{5}} \mathrm{e}^{\mathrm{x}} \mathrm{dx} \\ $$

Commented by mathmax by abdo last updated on 16/May/20

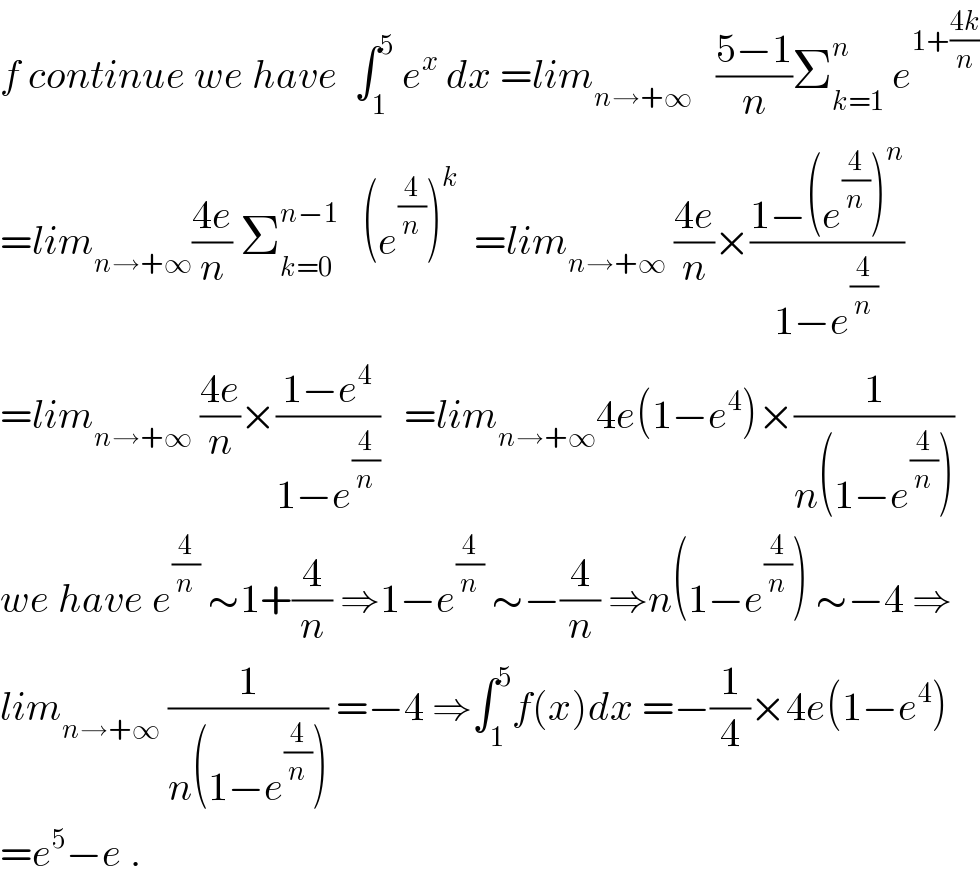
f continue we have ∫_1 ^5 e^x dx =lim_(n→+∞) ((5−1)/n)Σ_(k=1) ^n e^(1+((4k)/n)) =lim_(n→+∞) ((4e)/n) Σ_(k=0) ^(n−1) (e^(4/n) )^k =lim_(n→+∞) ((4e)/n)×((1−(e^(4/n) )^n )/(1−e^(4/n) )) =lim_(n→+∞) ((4e)/n)×((1−e^4 )/(1−e^(4/n) )) =lim_(n→+∞) 4e(1−e^4 )×(1/(n(1−e^(4/n) ))) we have e^(4/n) ∼1+(4/n) ⇒1−e^(4/n) ∼−(4/n) ⇒n(1−e^(4/n) ) ∼−4 ⇒ lim_(n→+∞) (1/(n(1−e^(4/n) ))) =−4 ⇒∫_1 ^5 f(x)dx =−(1/4)×4e(1−e^4 ) =e^5 −e .

$${f}\:{continue}\:{we}\:{have}\:\:\int_{\mathrm{1}} ^{\mathrm{5}} \:{e}^{{x}} \:{dx}\:={lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{5}−\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} \:{e}^{\mathrm{1}+\frac{\mathrm{4}{k}}{{n}}} \\ $$$$={lim}_{{n}\rightarrow+\infty} \frac{\mathrm{4}{e}}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\left({e}^{\frac{\mathrm{4}}{{n}}} \right)^{{k}} \:\:={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{4}{e}}{{n}}×\frac{\mathrm{1}−\left({e}^{\frac{\mathrm{4}}{{n}}} \right)^{{n}} }{\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} } \\ $$$$={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{4}{e}}{{n}}×\frac{\mathrm{1}−{e}^{\mathrm{4}} }{\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} }\:\:\:={lim}_{{n}\rightarrow+\infty} \mathrm{4}{e}\left(\mathrm{1}−{e}^{\mathrm{4}} \right)×\frac{\mathrm{1}}{{n}\left(\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} \right)} \\ $$$${we}\:{have}\:{e}^{\frac{\mathrm{4}}{{n}}} \:\sim\mathrm{1}+\frac{\mathrm{4}}{{n}}\:\Rightarrow\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} \:\sim−\frac{\mathrm{4}}{{n}}\:\Rightarrow{n}\left(\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} \right)\:\sim−\mathrm{4}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{{n}\left(\mathrm{1}−{e}^{\frac{\mathrm{4}}{{n}}} \right)}\:=−\mathrm{4}\:\Rightarrow\int_{\mathrm{1}} ^{\mathrm{5}} {f}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{4}{e}\left(\mathrm{1}−{e}^{\mathrm{4}} \right) \\ $$$$={e}^{\mathrm{5}} −{e}\:. \\ $$

Commented by Ar Brandon last updated on 16/May/20

Thanks ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com