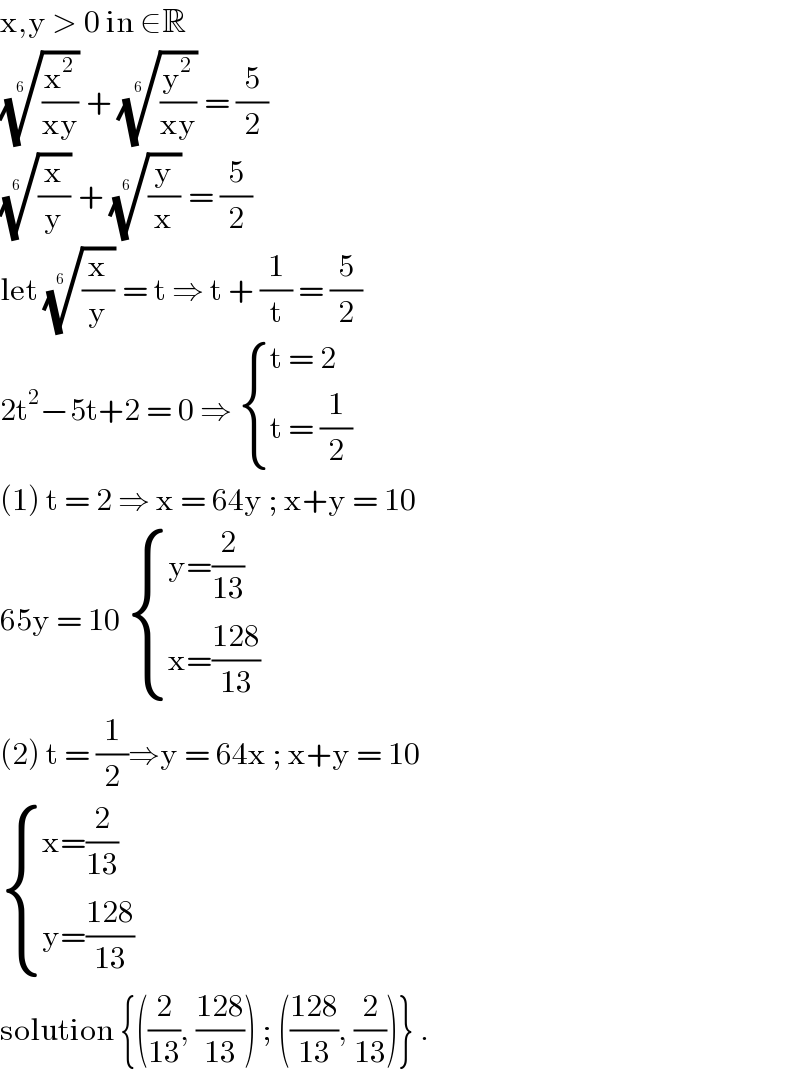Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 94174 by i jagooll last updated on 17/May/20

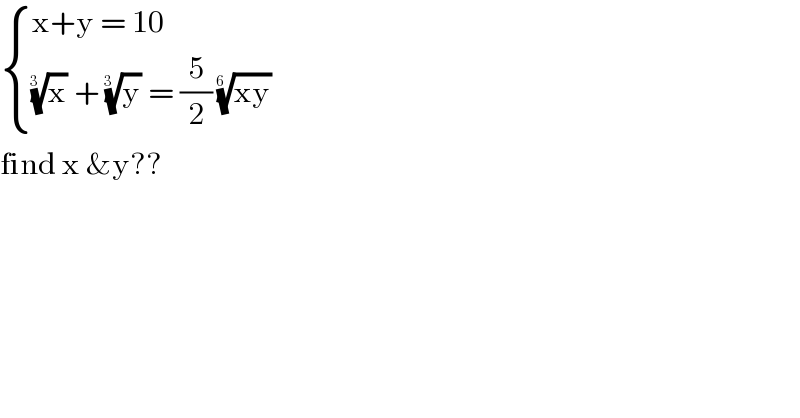
{ ((x+y = 10)),(((x)^(1/(3 )) + (y)^(1/(3 )) = (5/2) ((xy))^(1/(6 )) )) :} find x &y??

$$\begin{cases}{\mathrm{x}+\mathrm{y}\:=\:\mathrm{10}}\\{\sqrt[{\mathrm{3}\:\:}]{\mathrm{x}}\:+\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{y}}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\:\sqrt[{\mathrm{6}\:\:}]{\mathrm{xy}}}\end{cases}\: \\ $$ $$\mathrm{find}\:\mathrm{x}\:\&\mathrm{y}?? \\ $$

Commented bybehi83417@gmail.com last updated on 17/May/20

x=t^6 ,y=s^6 ⇒ { ((t^6 +s^6 =10)),((t^2 +s^2 =(5/2)ts)) :}⇒ { (((t^2 +s^2 )(t^4 −t^2 s^2 +s^4 )=10)),((t^2 +s^2 =(5/2)ts)) :} ⇒ { (((t^2 +s^2 )[(t^2 +s^2 )^2 −3t^2 s^2 ]=10)),((t^2 +s^2 =(5/2)ts)) :} ⇒(5/2)ts(((25)/4)t^2 s^2 −3t^2 s^2 )=10⇒t^3 s^3 =((16)/(13)) ⇒ { ((t^6 +s^6 =10)),((t^6 .s^6 =((256)/(169)))) :} ⇒z^2 −10z+((256)/(169))=0 ⇒z=(t^6 ∨s^6 )=5±(√(25−((256)/(169))))=5±((63)/(13)) ⇒ { ((x=t^6 =5±((63)/(13))=((128)/(13)),(2/(13)))),((y=s^6 =5±((63)/(13))=((128)/(13)),(2/(13)))) :}

$$\mathrm{x}=\mathrm{t}^{\mathrm{6}} ,\mathrm{y}=\mathrm{s}^{\mathrm{6}} \\ $$ $$\Rightarrow\begin{cases}{\mathrm{t}^{\mathrm{6}} +\mathrm{s}^{\mathrm{6}} =\mathrm{10}}\\{\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ts}}\end{cases}\Rightarrow\begin{cases}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{4}} −\mathrm{t}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} +\mathrm{s}^{\mathrm{4}} \right)=\mathrm{10}}\\{\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ts}}\end{cases} \\ $$ $$\Rightarrow\begin{cases}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} \right)\left[\left(\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{3t}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \right]=\mathrm{10}}\\{\mathrm{t}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ts}}\end{cases} \\ $$ $$\Rightarrow\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ts}\left(\frac{\mathrm{25}}{\mathrm{4}}\mathrm{t}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} −\mathrm{3t}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \right)=\mathrm{10}\Rightarrow\mathrm{t}^{\mathrm{3}} \mathrm{s}^{\mathrm{3}} =\frac{\mathrm{16}}{\mathrm{13}} \\ $$ $$\Rightarrow\begin{cases}{\mathrm{t}^{\mathrm{6}} +\mathrm{s}^{\mathrm{6}} =\mathrm{10}}\\{\mathrm{t}^{\mathrm{6}} .\mathrm{s}^{\mathrm{6}} =\frac{\mathrm{256}}{\mathrm{169}}}\end{cases}\:\:\:\:\Rightarrow\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{\mathrm{z}}+\frac{\mathrm{256}}{\mathrm{169}}=\mathrm{0} \\ $$ $$\Rightarrow\boldsymbol{\mathrm{z}}=\left(\boldsymbol{\mathrm{t}}^{\mathrm{6}} \vee\boldsymbol{\mathrm{s}}^{\mathrm{6}} \right)=\mathrm{5}\pm\sqrt{\mathrm{25}−\frac{\mathrm{256}}{\mathrm{169}}}=\mathrm{5}\pm\frac{\mathrm{63}}{\mathrm{13}} \\ $$ $$\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{t}^{\mathrm{6}} =\mathrm{5}\pm\frac{\mathrm{63}}{\mathrm{13}}=\frac{\mathrm{128}}{\mathrm{13}},\frac{\mathrm{2}}{\mathrm{13}}}\\{\mathrm{y}=\mathrm{s}^{\mathrm{6}} =\mathrm{5}\pm\frac{\mathrm{63}}{\mathrm{13}}=\frac{\mathrm{128}}{\mathrm{13}},\frac{\mathrm{2}}{\mathrm{13}}}\end{cases} \\ $$

Commented byi jagooll last updated on 17/May/20

thank you both

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Commented byhknkrc46 last updated on 17/May/20

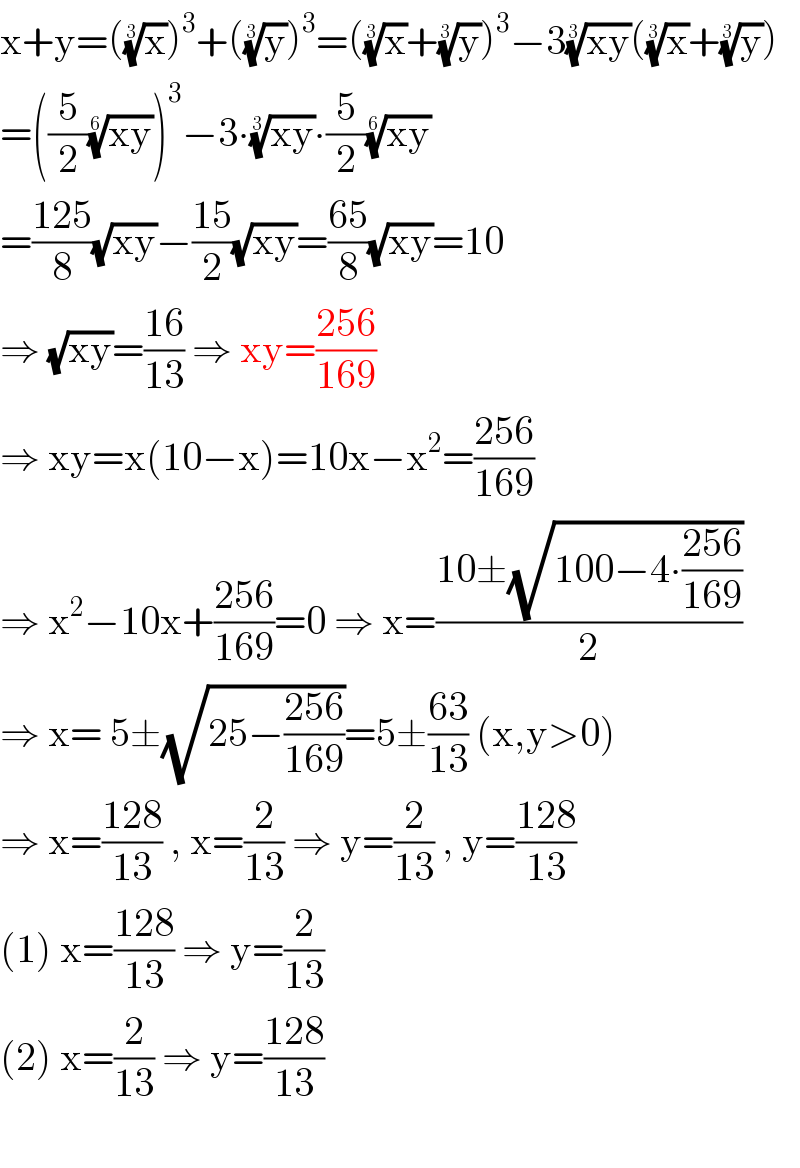
x+y=((x)^(1/3) )^3 +((y)^(1/3) )^3 =((x)^(1/3) +(y)^(1/3) )^3 −3((xy))^(1/3) ((x)^(1/3) +(y)^(1/3) ) =((5/2)((xy))^(1/6) )^3 −3∙((xy))^(1/3) ∙(5/2)((xy))^(1/6) =((125)/8)(√(xy))−((15)/2)(√(xy))=((65)/8)(√(xy))=10 ⇒ (√(xy))=((16)/(13)) ⇒ xy=((256)/(169)) ⇒ xy=x(10−x)=10x−x^2 =((256)/(169)) ⇒ x^2 −10x+((256)/(169))=0 ⇒ x=((10±(√(100−4∙((256)/(169)))))/2) ⇒ x= 5±(√(25−((256)/(169))))=5±((63)/(13)) (x,y>0) ⇒ x=((128)/(13)) , x=(2/(13)) ⇒ y=(2/(13)) , y=((128)/(13)) (1) x=((128)/(13)) ⇒ y=(2/(13)) (2) x=(2/(13)) ⇒ y=((128)/(13))

$$\mathrm{x}+\mathrm{y}=\left(\sqrt[{\mathrm{3}}]{\mathrm{x}}\right)^{\mathrm{3}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{y}}\right)^{\mathrm{3}} =\left(\sqrt[{\mathrm{3}}]{\mathrm{x}}+\sqrt[{\mathrm{3}}]{\mathrm{y}}\right)^{\mathrm{3}} −\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{xy}}\left(\sqrt[{\mathrm{3}}]{\mathrm{x}}+\sqrt[{\mathrm{3}}]{\mathrm{y}}\right) \\ $$ $$=\left(\frac{\mathrm{5}}{\mathrm{2}}\sqrt[{\mathrm{6}}]{\mathrm{xy}}\right)^{\mathrm{3}} −\mathrm{3}\centerdot\sqrt[{\mathrm{3}}]{\mathrm{xy}}\centerdot\frac{\mathrm{5}}{\mathrm{2}}\sqrt[{\mathrm{6}}]{\mathrm{xy}} \\ $$ $$=\frac{\mathrm{125}}{\mathrm{8}}\sqrt{\mathrm{xy}}−\frac{\mathrm{15}}{\mathrm{2}}\sqrt{\mathrm{xy}}=\frac{\mathrm{65}}{\mathrm{8}}\sqrt{\mathrm{xy}}=\mathrm{10} \\ $$ $$\Rightarrow\:\sqrt{\mathrm{xy}}=\frac{\mathrm{16}}{\mathrm{13}}\:\Rightarrow\:\mathrm{xy}=\frac{\mathrm{256}}{\mathrm{169}} \\ $$ $$\Rightarrow\:\mathrm{xy}=\mathrm{x}\left(\mathrm{10}−\mathrm{x}\right)=\mathrm{10x}−\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{256}}{\mathrm{169}} \\ $$ $$\Rightarrow\:\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\frac{\mathrm{256}}{\mathrm{169}}=\mathrm{0}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}\centerdot\frac{\mathrm{256}}{\mathrm{169}}}}{\mathrm{2}} \\ $$ $$\Rightarrow\:\mathrm{x}=\:\mathrm{5}\pm\sqrt{\mathrm{25}−\frac{\mathrm{256}}{\mathrm{169}}}=\mathrm{5}\pm\frac{\mathrm{63}}{\mathrm{13}}\:\left(\mathrm{x},\mathrm{y}>\mathrm{0}\right) \\ $$ $$\Rightarrow\:\mathrm{x}=\frac{\mathrm{128}}{\mathrm{13}}\:,\:\mathrm{x}=\frac{\mathrm{2}}{\mathrm{13}}\:\Rightarrow\:\mathrm{y}=\frac{\mathrm{2}}{\mathrm{13}}\:,\:\mathrm{y}=\frac{\mathrm{128}}{\mathrm{13}} \\ $$ $$\left(\mathrm{1}\right)\:\mathrm{x}=\frac{\mathrm{128}}{\mathrm{13}}\:\Rightarrow\:\mathrm{y}=\frac{\mathrm{2}}{\mathrm{13}} \\ $$ $$\left(\mathrm{2}\right)\:\mathrm{x}=\frac{\mathrm{2}}{\mathrm{13}}\:\Rightarrow\:\mathrm{y}=\frac{\mathrm{128}}{\mathrm{13}} \\ $$ $$ \\ $$

Answered by john santu last updated on 17/May/20

x,y > 0 in ∈R ((x^2 /(xy)))^(1/(6 )) + ((y^2 /(xy)))^(1/(6 )) = (5/2) ((x/y))^(1/(6 )) + ((y/x))^(1/(6 )) = (5/2) let ((x/y))^(1/(6 )) = t ⇒ t + (1/t) = (5/2) 2t^2 −5t+2 = 0 ⇒ { ((t = 2)),((t = (1/2))) :} (1) t = 2 ⇒ x = 64y ; x+y = 10 65y = 10 { ((y=(2/(13)))),((x=((128)/(13)))) :} (2) t = (1/2)⇒y = 64x ; x+y = 10 { ((x=(2/(13)))),((y=((128)/(13)))) :} solution {((2/(13)), ((128)/(13))) ; (((128)/(13)), (2/(13)))} .

$$\mathrm{x},\mathrm{y}\:>\:\mathrm{0}\:\mathrm{in}\:\in\mathbb{R} \\ $$ $$\sqrt[{\mathrm{6}\:\:}]{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{xy}}}\:+\:\sqrt[{\mathrm{6}\:\:}]{\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}}}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$ $$\sqrt[{\mathrm{6}\:\:}]{\frac{\mathrm{x}}{\mathrm{y}}}\:+\:\sqrt[{\mathrm{6}\:\:}]{\frac{\mathrm{y}}{\mathrm{x}}}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$ $$\mathrm{let}\:\sqrt[{\mathrm{6}\:\:}]{\frac{\mathrm{x}}{\mathrm{y}}}\:=\:\mathrm{t}\:\Rightarrow\:\mathrm{t}\:+\:\frac{\mathrm{1}}{\mathrm{t}}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$ $$\mathrm{2t}^{\mathrm{2}} −\mathrm{5t}+\mathrm{2}\:=\:\mathrm{0}\:\Rightarrow\:\begin{cases}{\mathrm{t}\:=\:\mathrm{2}}\\{\mathrm{t}\:=\:\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$ $$\left(\mathrm{1}\right)\:\mathrm{t}\:=\:\mathrm{2}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{64y}\:;\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{10}\: \\ $$ $$\mathrm{65y}\:=\:\mathrm{10}\:\begin{cases}{\mathrm{y}=\frac{\mathrm{2}}{\mathrm{13}}}\\{\mathrm{x}=\frac{\mathrm{128}}{\mathrm{13}}}\end{cases} \\ $$ $$\left(\mathrm{2}\right)\:\mathrm{t}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{y}\:=\:\mathrm{64x}\:;\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{10} \\ $$ $$\begin{cases}{\mathrm{x}=\frac{\mathrm{2}}{\mathrm{13}}}\\{\mathrm{y}=\frac{\mathrm{128}}{\mathrm{13}}}\end{cases} \\ $$ $$\mathrm{solution}\:\left\{\left(\frac{\mathrm{2}}{\mathrm{13}},\:\frac{\mathrm{128}}{\mathrm{13}}\right)\:;\:\left(\frac{\mathrm{128}}{\mathrm{13}},\:\frac{\mathrm{2}}{\mathrm{13}}\right)\right\}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com