Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 94184 by MJS last updated on 17/May/20

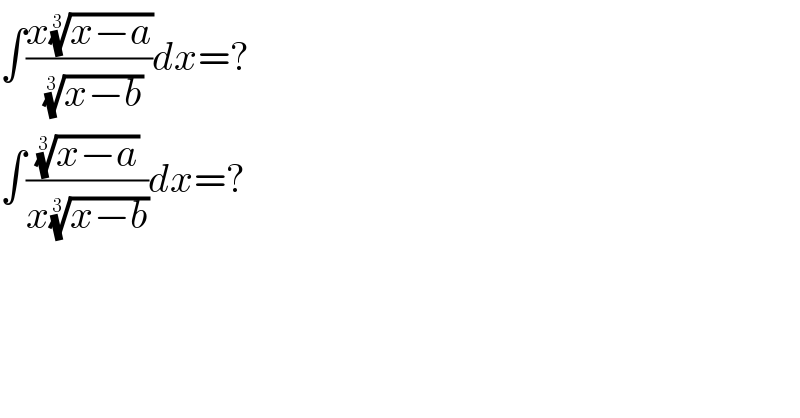
∫((x((x−a))^(1/3) )/((x−b))^(1/3) )dx=? ∫(((x−a))^(1/3) /(x((x−b))^(1/3) ))dx=?

$$\int\frac{{x}\sqrt[{\mathrm{3}}]{{x}−{a}}}{\sqrt[{\mathrm{3}}]{{x}−{b}}}{dx}=? \\ $$$$\int\frac{\sqrt[{\mathrm{3}}]{{x}−{a}}}{{x}\sqrt[{\mathrm{3}}]{{x}−{b}}}{dx}=? \\ $$

Commented by MJS last updated on 17/May/20

I can solve both but I want to know if there's an easier path. will post my solutions later.

Answered by  M±th+et+s last updated on 04/Jun/20

∫x((1−((a−b)/(x−b))))^(1/3) dx,((a−b)/(x−b))=u^3 ⇒dx=(((a−b)(3u^2 ))/((1−u^3 )^2 ))du I=∫[((a−b)/(1−u^3 ))+b][(((a−b)(3u^2 ))/((1−u^3 )^2 ))](u)du =(a−b)^2 ∫((3u^2 )/((1−u^3 )^3 ))du+b(a−b)∫((3u^2 )/((1−u^3 )^2 ))du I_1 =(1/2)∫[(u)(((2)(3u^2 ))/((1−u^3 )^3 ))+(1/((1−u^3 )^2 ))−(1/((1−u^3 )^2 ))]du I_1 =(1/2)∫d((u/((1−u^3 )^2 )))−(1/2)∫(du/((1−u^3 )^2 ))du I_3 =∫((1−u^3 +u^3 )/((1−u^3 )^2 ))du=∫(1/(1−u^3 ))du+(1/2)∫((−2u−(1/u^2 )+(1/u^2 ))/([(1/u)−u^2 ]^2 ))du I_3 =∫(1/((1−u)(1+u+u^2 )))du−(1/2)∫((−(1/u^2 )−2u)/([(1/u)−u^2 ]^2 ))du−(1/2)∫(1/(u^2 [(1/u)−u^2 ]^2 ))du I_3 =∫((1/3)/(1−u))du+∫(((1/3)u+(2/3))/(u^2 +u+1))du+(1/(2((1/u)−u^2 )))−(1/2)∫(1/((1−u^3 )^2 ))du I_3 =(1/3)∫d(ln∣1−u∣)+(1/6)∫((2u+1−1)/(u^2 +u+1))du+(2/3)∫(1/(u^2 +u+1))du+(1/(2((1/u)−u^2 )))−(1/2)I_3 (3/2)I_3 =(1/3)ln∣1−u∣+(1/6)ln∣u^2 +u+1∣+(2/3)tan^(−1) (((2u+(1/2))/(√3)))+(1/(2((1/u)−u^2 ))) I_1 =(u/((1−u^3 )^2 ))−(1/2)I_3 I_2 =(3/2)∫((1−u^3 +3u^3 −1)/((1−u^3 )^2 ))du=(3/2)∫((1−u^3 −(u)(−3u^2 ))/((1−u^3 )^2 ))du−(3/2)∫(1/((1−u^3 )^2 ))du I_2 =(3/2)∫d((u/(1−u^3 )))−(3/2)I_3 I=I_1 +I_2 +c

$$\int{x}\sqrt[{\mathrm{3}}]{\mathrm{1}−\frac{{a}−{b}}{{x}−{b}}}{dx},\frac{{a}−{b}}{{x}−{b}}={u}^{\mathrm{3}} \Rightarrow{dx}=\frac{\left({a}−{b}\right)\left(\mathrm{3}{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du} \\ $$$${I}=\int\left[\frac{{a}−{b}}{\mathrm{1}−{u}^{\mathrm{3}} }+{b}\right]\left[\frac{\left({a}−{b}\right)\left(\mathrm{3}{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }\right]\left({u}\right){du} \\ $$$$=\left({a}−{b}\right)^{\mathrm{2}} \int\frac{\mathrm{3}{u}^{\mathrm{2}} }{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{3}} }{du}+{b}\left({a}−{b}\right)\int\frac{\mathrm{3}{u}^{\mathrm{2}} }{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\left[\left({u}\right)\frac{\left(\mathrm{2}\right)\left(\mathrm{3}{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }\right]{du} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int{d}\left(\frac{{u}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{3}} =\int\frac{\mathrm{1}−{u}^{\mathrm{3}} +{u}^{\mathrm{3}} }{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du}=\int\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{3}} }{du}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}{u}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{\left[\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right]^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{3}} =\int\frac{\mathrm{1}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}+{u}^{\mathrm{2}} \right)}{du}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }−\mathrm{2}{u}}{\left[\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right]^{\mathrm{2}} }{du}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} \left[\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right]^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{3}} =\int\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−{u}}{du}+\int\frac{\frac{\mathrm{1}}{\mathrm{3}}{u}+\frac{\mathrm{2}}{\mathrm{3}}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}+\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}}\int{d}\left({ln}\mid\mathrm{1}−{u}\mid\right)+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{u}+\mathrm{1}−\mathrm{1}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}+\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{3}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\mathrm{1}−{u}\mid+\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{u}^{\mathrm{2}} +{u}+\mathrm{1}\mid+\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{u}+\frac{\mathrm{1}}{\mathrm{2}}}{\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}}{{u}}−{u}^{\mathrm{2}} \right)} \\ $$$${I}_{\mathrm{1}} =\frac{{u}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}−{u}^{\mathrm{3}} +\mathrm{3}{u}^{\mathrm{3}} −\mathrm{1}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du}=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}−{u}^{\mathrm{3}} −\left({u}\right)\left(−\mathrm{3}{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left(\mathrm{1}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }{du} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}}\int{d}\left(\frac{{u}}{\mathrm{1}−{u}^{\mathrm{3}} }\right)−\frac{\mathrm{3}}{\mathrm{2}}{I}_{\mathrm{3}} \\ $$$$ \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{c} \\ $$$$ \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 04/Jun/20

let I =∫ (1/x)(^3 (√((x−a)/(x−b))))dx changement^3 (√((x−a)/(x−b)))=t give ((x−a)/(x−b)) =t^3 ⇒ x−a =t^3 x−bt^3 ⇒(1−t^3 )x =a−bt^3 ⇒x =((a−bt^3 )/(1−t^3 )) =((bt^3 −a)/(t^3 −1)) (dx/dt) =((3bt^2 (t^3 −1)−3t^2 (bt^3 −a))/((t^3 −1)^2 )) =((3bt^5 −3bt^2 −3bt^5 +3at^2 )/((t^3 −1)^2 )) ⇒ I =∫ ((t^3 −1)/(bt^3 −a))×t ×(((3a−3b)t^2 )/((t^3 −1)^2 )) dt =(3a−3b) ∫ (t^3 /((bt^3 −a)(t^3 −1)))dt =((3a−3b)/b) ∫ (t^3 /((t^3 −(^3 (√(a/b)))^3 )(t^3 −1)))dt let α =^3 (√(a/b)) ⇒ I =((3a−3b)/b) ∫ (t^3 /((t^3 −α^3 )(t^3 −1)))dt let decompose F(t) =(t^3 /((t^3 −α^3 )(t^3 −1))) ⇒F(t) =(t^3 /((t−α)(t^2 +αt +α^2 )(t−1)(t^2 +t +1))) =(a/(t−α)) +(b/(t−1)) +((ct +d)/(t^2 +αt +α^2 )) +((et +f)/(t^2 +t+1)) ⇒ ∫ F(t)dt =aln∣t−α∣ +bln∣t−1∣ +∫ ((ct +d)/(t^2 +αt +α^2 ))dt +∫ ((et +f)/(t^2 +t +1))dt rest to calculate the coefficients...be continued...

$$\mathrm{let}\:\mathrm{I}\:=\int\:\frac{\mathrm{1}}{\mathrm{x}}\left(^{\mathrm{3}} \sqrt{\frac{\mathrm{x}−\mathrm{a}}{\mathrm{x}−\mathrm{b}}}\right)\mathrm{dx}\:\mathrm{changement}\:^{\mathrm{3}} \sqrt{\frac{\mathrm{x}−\mathrm{a}}{\mathrm{x}−\mathrm{b}}}=\mathrm{t}\:\mathrm{give}\:\frac{\mathrm{x}−\mathrm{a}}{\mathrm{x}−\mathrm{b}}\:=\mathrm{t}^{\mathrm{3}} \:\Rightarrow \\ $$$$\mathrm{x}−\mathrm{a}\:=\mathrm{t}^{\mathrm{3}} \mathrm{x}−\mathrm{bt}^{\mathrm{3}} \:\Rightarrow\left(\mathrm{1}−\mathrm{t}^{\mathrm{3}} \right)\mathrm{x}\:=\mathrm{a}−\mathrm{bt}^{\mathrm{3}} \:\Rightarrow\mathrm{x}\:=\frac{\mathrm{a}−\mathrm{bt}^{\mathrm{3}} }{\mathrm{1}−\mathrm{t}^{\mathrm{3}} }\:=\frac{\mathrm{bt}^{\mathrm{3}} −\mathrm{a}}{\mathrm{t}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{3bt}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)−\mathrm{3t}^{\mathrm{2}} \left(\mathrm{bt}^{\mathrm{3}} −\mathrm{a}\right)}{\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3bt}^{\mathrm{5}} −\mathrm{3bt}^{\mathrm{2}} −\mathrm{3bt}^{\mathrm{5}} +\mathrm{3at}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{bt}^{\mathrm{3}} −\mathrm{a}}×\mathrm{t}\:×\frac{\left(\mathrm{3a}−\mathrm{3b}\right)\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dt}\:=\left(\mathrm{3a}−\mathrm{3b}\right)\:\int\:\:\frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{bt}^{\mathrm{3}} −\mathrm{a}\right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{3a}−\mathrm{3b}}{\mathrm{b}}\:\int\:\:\frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{t}^{\mathrm{3}} −\left(^{\mathrm{3}} \sqrt{\frac{\mathrm{a}}{\mathrm{b}}}\right)^{\mathrm{3}} \right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)}\mathrm{dt}\:\:\:\mathrm{let}\:\alpha\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{a}}{\mathrm{b}}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{3a}−\mathrm{3b}}{\mathrm{b}}\:\int\:\:\frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{t}^{\mathrm{3}} −\alpha^{\mathrm{3}} \right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)}\mathrm{dt}\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{t}^{\mathrm{3}} −\alpha^{\mathrm{3}} \right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{t}−\alpha\right)\left(\mathrm{t}^{\mathrm{2}} \:+\alpha\mathrm{t}\:+\alpha^{\mathrm{2}} \right)\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{t}−\alpha}\:+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{1}}\:+\frac{\mathrm{ct}\:+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} \:+\alpha\mathrm{t}\:+\alpha^{\mathrm{2}} }\:+\frac{\mathrm{et}\:+\mathrm{f}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{aln}\mid\mathrm{t}−\alpha\mid\:+\mathrm{bln}\mid\mathrm{t}−\mathrm{1}\mid\:+\int\:\frac{\mathrm{ct}\:+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} \:+\alpha\mathrm{t}\:+\alpha^{\mathrm{2}} }\mathrm{dt}\:+\int\:\:\frac{\mathrm{et}\:+\mathrm{f}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}\:+\mathrm{1}}\mathrm{dt} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{coefficients}...\mathrm{be}\:\mathrm{continued}... \\ $$

Answered by MJS last updated on 05/Jun/20

∫((x((x−a))^(1/3) )/((x−b))^(1/3) )dx= [t=(((x−a))^(1/3) /((x−b))^(1/3) ) → dx=(3/(a−b))(x−a)^(2/3) (x−b)^(4/3) ] =3(a−b)∫((t^3 (bt^3 −a))/((t^3 −1)^3 ))dt= [Ostrogradski] =((a−b)/(6(t^3 −1)^2 ))((a−7b)t^3 +2(a+2b))t+(((a−b)(a+2b))/3)∫(dt/(t^3 −1))= and I have shown that ∫(dt/(t^3 −1))=(1/6)ln (((t−1)^2 )/(t^2 +t+1)) −((√3)/3)arctan (((√3)(2t+1))/3)

$$\int\frac{{x}\sqrt[{\mathrm{3}}]{{x}−{a}}}{\sqrt[{\mathrm{3}}]{{x}−{b}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt[{\mathrm{3}}]{{x}−{a}}}{\sqrt[{\mathrm{3}}]{{x}−{b}}}\:\rightarrow\:{dx}=\frac{\mathrm{3}}{{a}−{b}}\left({x}−{a}\right)^{\mathrm{2}/\mathrm{3}} \left({x}−{b}\right)^{\mathrm{4}/\mathrm{3}} \right] \\ $$$$=\mathrm{3}\left({a}−{b}\right)\int\frac{{t}^{\mathrm{3}} \left({bt}^{\mathrm{3}} −{a}\right)}{\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{{a}−{b}}{\mathrm{6}\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }\left(\left({a}−\mathrm{7}{b}\right){t}^{\mathrm{3}} +\mathrm{2}\left({a}+\mathrm{2}{b}\right)\right){t}+\frac{\left({a}−{b}\right)\left({a}+\mathrm{2}{b}\right)}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{3}} −\mathrm{1}}= \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{have}\:\mathrm{shown}\:\mathrm{that} \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{3}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}} \\ $$

Answered by MJS last updated on 05/Jun/20

∫(((x−a))^(1/3) /(x((x−b))^(1/3) ))dx= [t=(((x−a))^(1/3) /((x−b))^(1/3) ) → dx=(3/(a−b))(x−a)^(2/3) (x−b)^(4/3) dt] =3(a−b)∫(t^3 /((t^3 −1)(bt^3 −a)))dt= [let a=bc^3 ⇔ c=((a/b))^(1/3) ] =3(c^3 −1)∫(t^3 /((t^3 −1)(t^3 −c^3 )))dt= =c∫(dt/(t−c))−∫(dt/(t−1))−c∫((t+2c)/(t^2 +ct+c^2 ))dt+∫((t+2)/(t^2 +t+1))dt= ... =(1/2)ln ((t^2 +t+1)/((t−1)^2 )) +(c/2)ln (((t−c)^2 )/(t^2 +ct+c^2 )) + +(√3)arctan (((√3)(2t+1))/3) −c(√3)arctan (((√3)(2t+c))/3)

$$\int\frac{\sqrt[{\mathrm{3}}]{{x}−{a}}}{{x}\sqrt[{\mathrm{3}}]{{x}−{b}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt[{\mathrm{3}}]{{x}−{a}}}{\sqrt[{\mathrm{3}}]{{x}−{b}}}\:\rightarrow\:{dx}=\frac{\mathrm{3}}{{a}−{b}}\left({x}−{a}\right)^{\mathrm{2}/\mathrm{3}} \left({x}−{b}\right)^{\mathrm{4}/\mathrm{3}} {dt}\right] \\ $$$$=\mathrm{3}\left({a}−{b}\right)\int\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{3}} −\mathrm{1}\right)\left({bt}^{\mathrm{3}} −{a}\right)}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{let}\:{a}={bc}^{\mathrm{3}} \:\Leftrightarrow\:{c}=\sqrt[{\mathrm{3}}]{\frac{{a}}{{b}}}\right] \\ $$$$=\mathrm{3}\left({c}^{\mathrm{3}} −\mathrm{1}\right)\int\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{3}} −\mathrm{1}\right)\left({t}^{\mathrm{3}} −{c}^{\mathrm{3}} \right)}{dt}= \\ $$$$={c}\int\frac{{dt}}{{t}−{c}}−\int\frac{{dt}}{{t}−\mathrm{1}}−{c}\int\frac{{t}+\mathrm{2}{c}}{{t}^{\mathrm{2}} +{ct}+{c}^{\mathrm{2}} }{dt}+\int\frac{{t}+\mathrm{2}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$... \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{\mathrm{2}}\mathrm{ln}\:\frac{\left({t}−{c}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +{ct}+{c}^{\mathrm{2}} }\:+ \\ $$$$\:\:\:\:\:+\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\:−{c}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+{c}\right)}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com