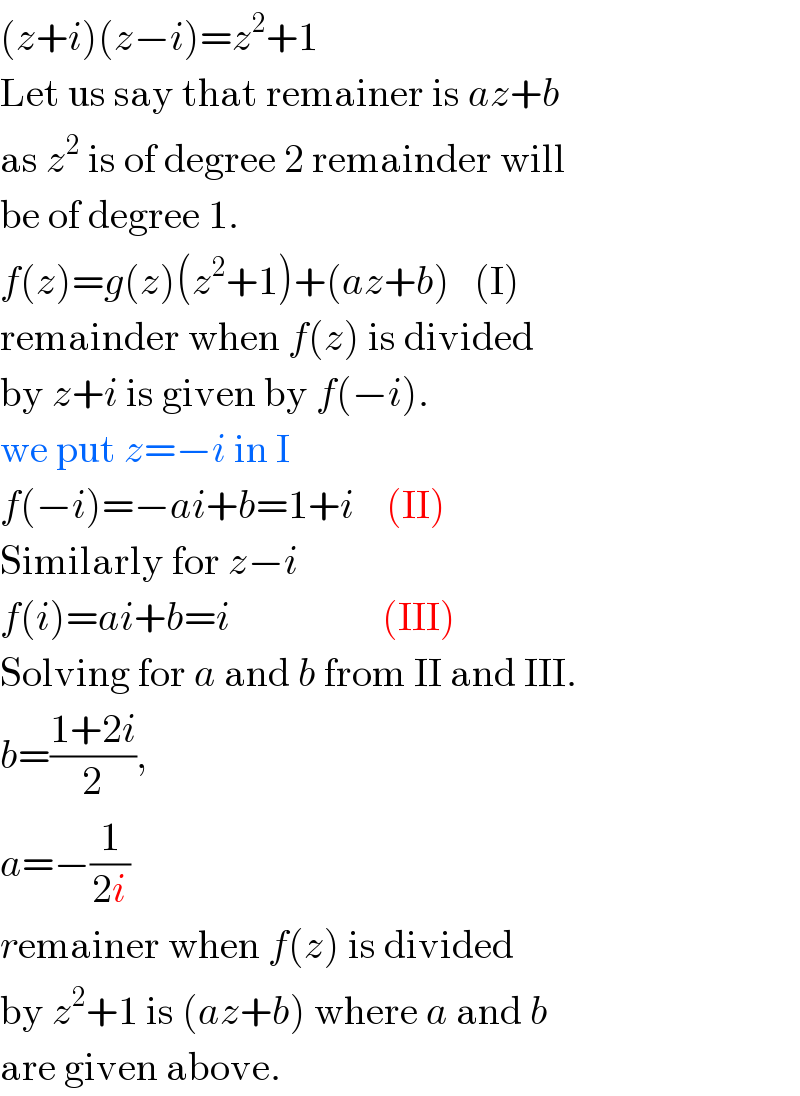Question and Answers Forum
Question Number 94193 by seedhamaieng@gmail.com last updated on 17/May/20

Commented by seedhamaieng@gmail.com last updated on 17/May/20
translate into Hind language Question no 7
Commented by seedhamaieng@gmail.com last updated on 17/May/20
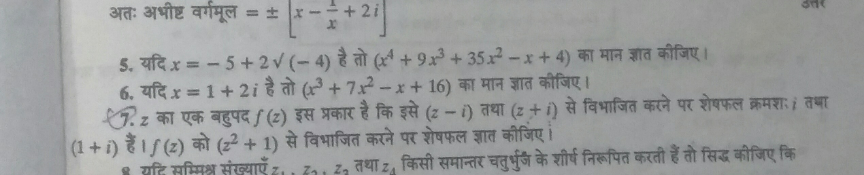
Commented by seedhamaieng@gmail.com last updated on 17/May/20
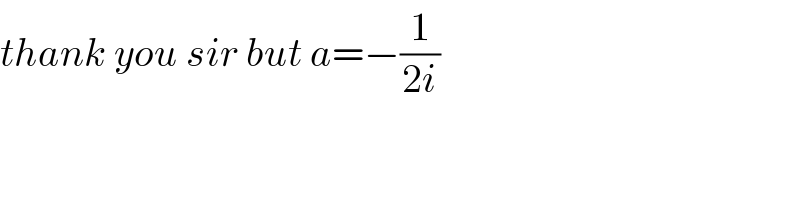
Commented by prakash jain last updated on 17/May/20

Commented by prakash jain last updated on 17/May/20