Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 94257 by pete last updated on 17/May/20

$$\mathrm{If}{9\mathrm{y}}^2+\frac{1}{{\mathrm{y}}^2}=3,\mathrm{then}\mathrm{find}\mathrm{the}\mathrm{value}\mathrm{of}$$$${27\mathrm{y}}^3+\frac{1}{{\mathrm{y}}^3}$$

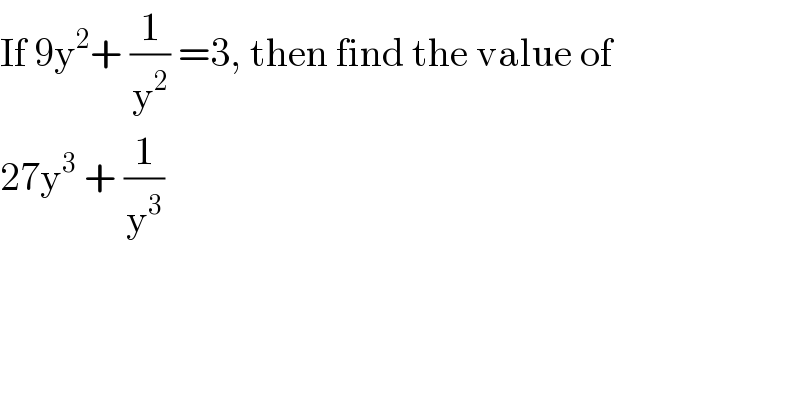
Answered by niroj last updated on 17/May/20

$${(3\mathrm{y}+\frac{1}{\mathrm{y}})}^2-2.3\mathrm{y}.\frac{1}{\mathrm{y}}={9\mathrm{y}}^2+\frac{1}{{\mathrm{y}}^2}$$$${(3\mathrm{y}+\frac{1}{\mathrm{y}})}^2=3+6$$$$3\mathrm{y}+\frac{1}{\mathrm{y}}=3$$$$\mathrm{now},$$$${(3\mathrm{y}+\frac{1}{\mathrm{y}})}^3={\left(3\mathrm{y}\right)}^3+{\left(\frac{1}{\mathrm{y}}\right)}^3+3.3\mathrm{y}.\frac{1}{\mathrm{y}}(3\mathrm{y}+\frac{1}{\mathrm{y}})$$$$={27\mathrm{y}}^3+\frac{1}{{\mathrm{y}}^3}+9.3$$$${27\mathrm{y}}^3+\frac{1}{{\mathrm{y}}^3}={(3\mathrm{y}+\frac{1}{\mathrm{y}})}^3-27$$$$=3^3-3^3=0$$

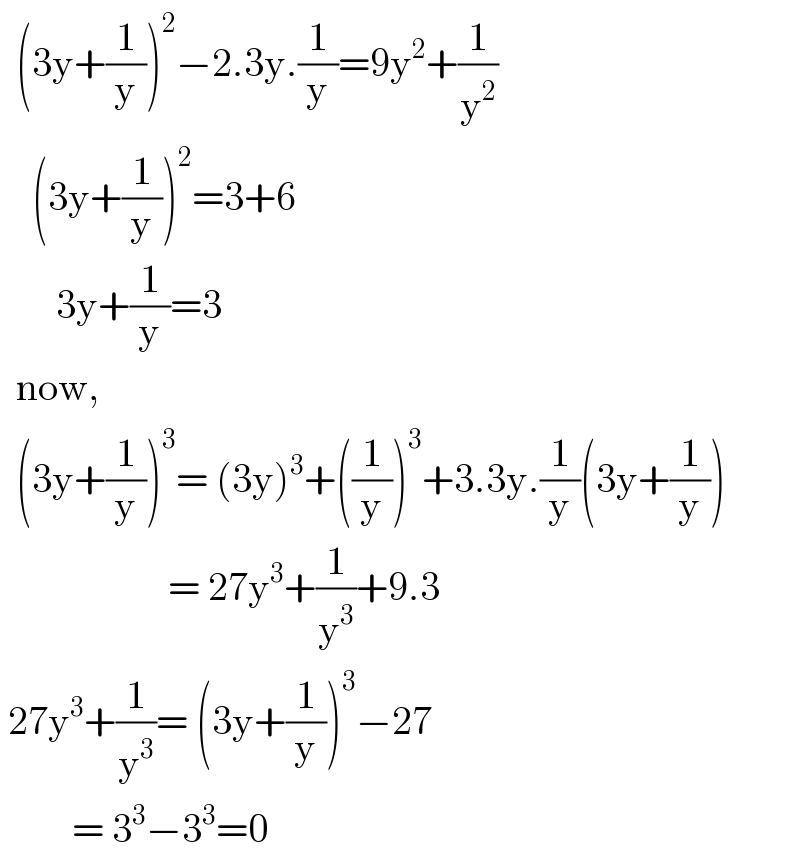
Commented by pete last updated on 17/May/20

$$\mathrm{Thanks}\mathrm{very}\mathrm{much}\mathrm{senior}.$$

Commented by niroj last updated on 17/May/20

������

Answered by Ar Brandon last updated on 17/May/20

$${\left(3\mathrm{y}\right)}^2+{\left(\frac{1}{\mathrm{y}}\right)}^2={(3\mathrm{y}+\frac{1}{\mathrm{y}})}^2-6=3$$$$\Rightarrow 3\mathrm{y}+\frac{1}{\mathrm{y}}=\pm 3$$$$\Rightarrow {27\mathrm{y}}^3+\frac{1}{{\mathrm{y}}^3}=(3\mathrm{y}+\frac{1}{\mathrm{y}})[{(3\mathrm{y}+\frac{1}{\mathrm{y}})}^2-9]=(\pm 3)[{(\pm 3)}^2-9]=0$$

Commented by pete last updated on 17/May/20

$$\mathrm{thanks}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com