Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 94269 by LPM last updated on 17/May/20

Commented by prakash jain last updated on 17/May/20

ln (1+x)=Σ_(n=1) ^∞ (x^n /n)(−1)^(n+1) ((ln (1+x))/x)=Σ_(n=0) ^∞ (x^n /(n+1))(−1)^n ∫_0 ^1 Σ_(n=0) ^∞ (x^n /(n+1))(−1)^n = [x−(x^2 /2^2 )+(x^3 /3^2 )−+...]_0 ^1 =1−(1/2^2 )+(1/3^2 )−+...=(π^2 /(12))

$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{{x}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}+\mathrm{1}}\left(−\mathrm{1}\right)^{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}+\mathrm{1}}\left(−\mathrm{1}\right)^{{n}} = \\ $$$$\left[{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{x}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{2}} }−+...\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }−+...=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by mathmax by abdo last updated on 17/May/20

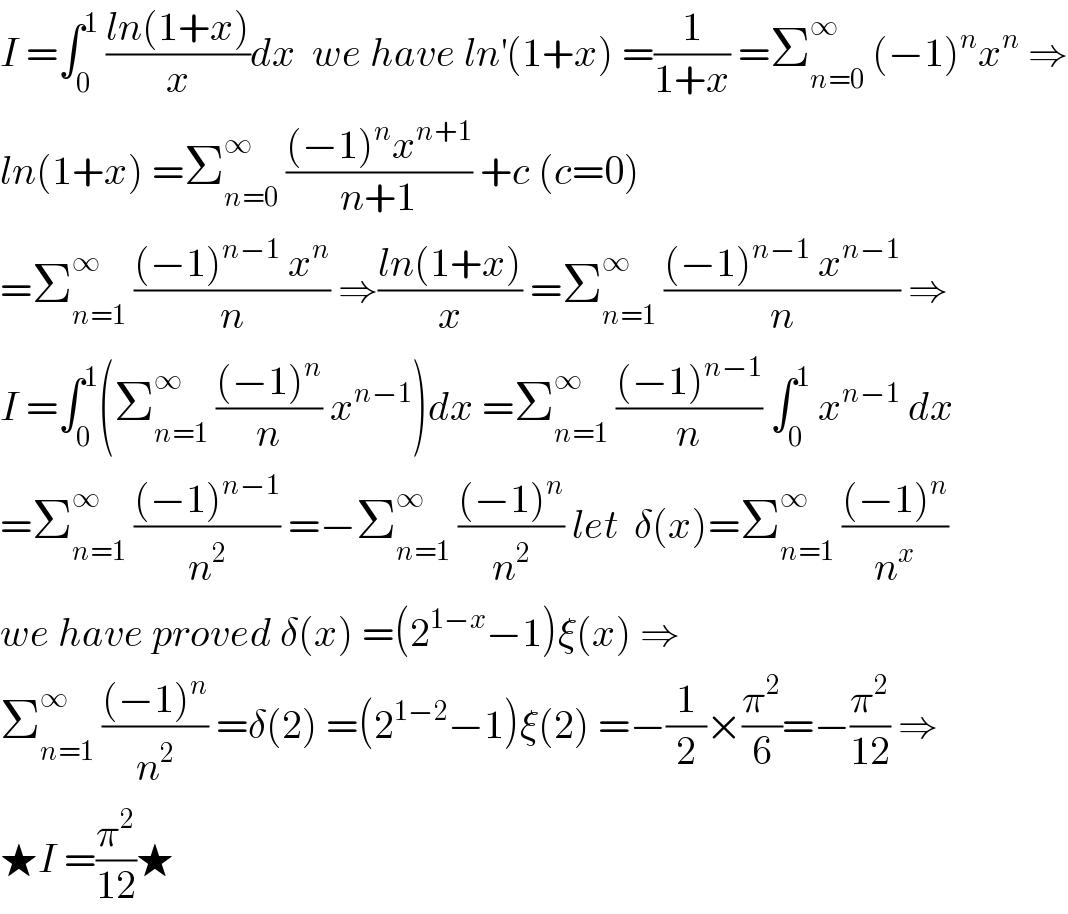
I =∫_0 ^1 ((ln(1+x))/x)dx we have ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒((ln(1+x))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) x^(n−1) )/n) ⇒ I =∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^n )/n) x^(n−1) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 x^(n−1) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) let δ(x)=Σ_(n=1) ^∞ (((−1)^n )/n^x ) we have proved δ(x) =(2^(1−x) −1)ξ(x) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =δ(2) =(2^(1−2) −1)ξ(2) =−(1/2)×(π^2 /6)=−(π^2 /(12)) ⇒ ★I =(π^2 /(12))★

$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}\:\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\:\left({c}=\mathrm{0}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}} }{{n}}\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}−\mathrm{1}} }{{n}}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}−\mathrm{1}} \right){dx}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}−\mathrm{1}} \:{dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:{let}\:\:\delta\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{x}} } \\ $$$${we}\:{have}\:{proved}\:\delta\left({x}\right)\:=\left(\mathrm{2}^{\mathrm{1}−{x}} −\mathrm{1}\right)\xi\left({x}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\delta\left(\mathrm{2}\right)\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\bigstar{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\bigstar \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com