
Question and Answers Forum
Question Number 94310 by mathmax by abdo last updated on 18/May/20
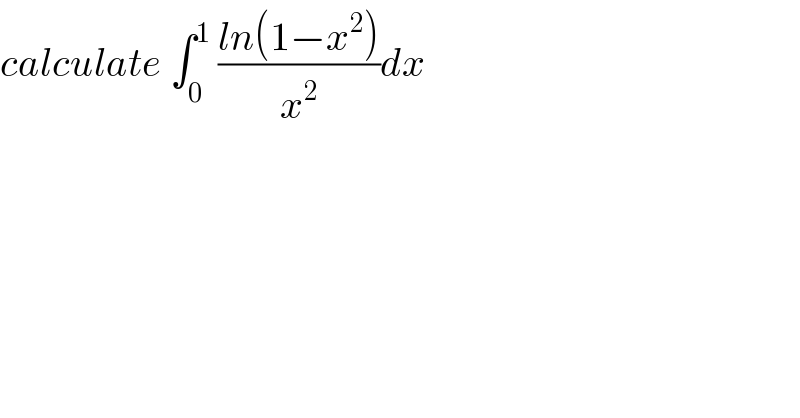
Answered by mathmax by abdo last updated on 19/May/20
![another way by parts u^′ =(1/x^2 ) and v =ln(1−x^2 ) ⇒ I =[(1−(1/x))ln(1−x^2 )]_0 ^1 −∫_0 ^1 (1−(1/x))×((−2x)/(1−x^2 ))dx =0 +2 ∫_0 ^1 ((x−1)/(1−x^2 ))dx =−2 ∫_0 ^1 ((1−x)/((1−x)(1+x)))dx =−2∫_0 ^1 (dx/(1+x)) =−2[ln∣1+x∣]_0 ^1 =−2ln(2) ⇒ ★ I =−2ln(2)★](Q94569.png)
Answered by mathmax by abdo last updated on 19/May/20
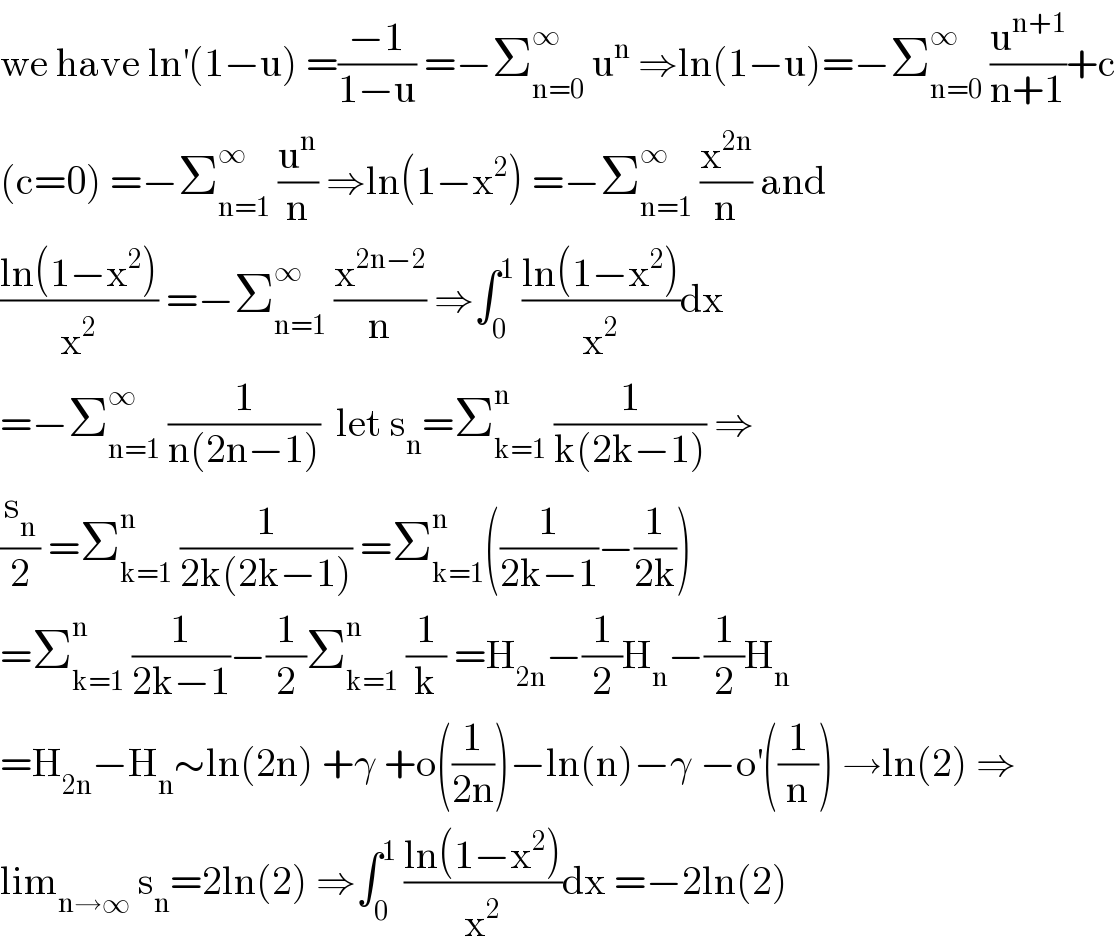
| ||
Question and Answers Forum | ||
Question Number 94310 by mathmax by abdo last updated on 18/May/20 | ||
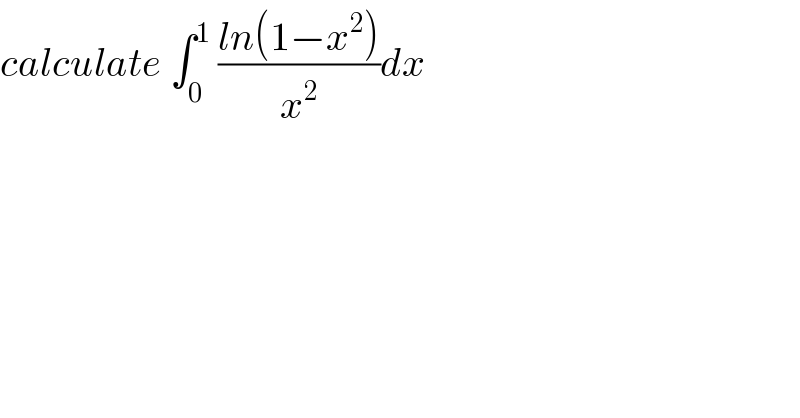 | ||
Answered by mathmax by abdo last updated on 19/May/20 | ||
![another way by parts u^′ =(1/x^2 ) and v =ln(1−x^2 ) ⇒ I =[(1−(1/x))ln(1−x^2 )]_0 ^1 −∫_0 ^1 (1−(1/x))×((−2x)/(1−x^2 ))dx =0 +2 ∫_0 ^1 ((x−1)/(1−x^2 ))dx =−2 ∫_0 ^1 ((1−x)/((1−x)(1+x)))dx =−2∫_0 ^1 (dx/(1+x)) =−2[ln∣1+x∣]_0 ^1 =−2ln(2) ⇒ ★ I =−2ln(2)★](Q94569.png) | ||
| ||
Answered by mathmax by abdo last updated on 19/May/20 | ||
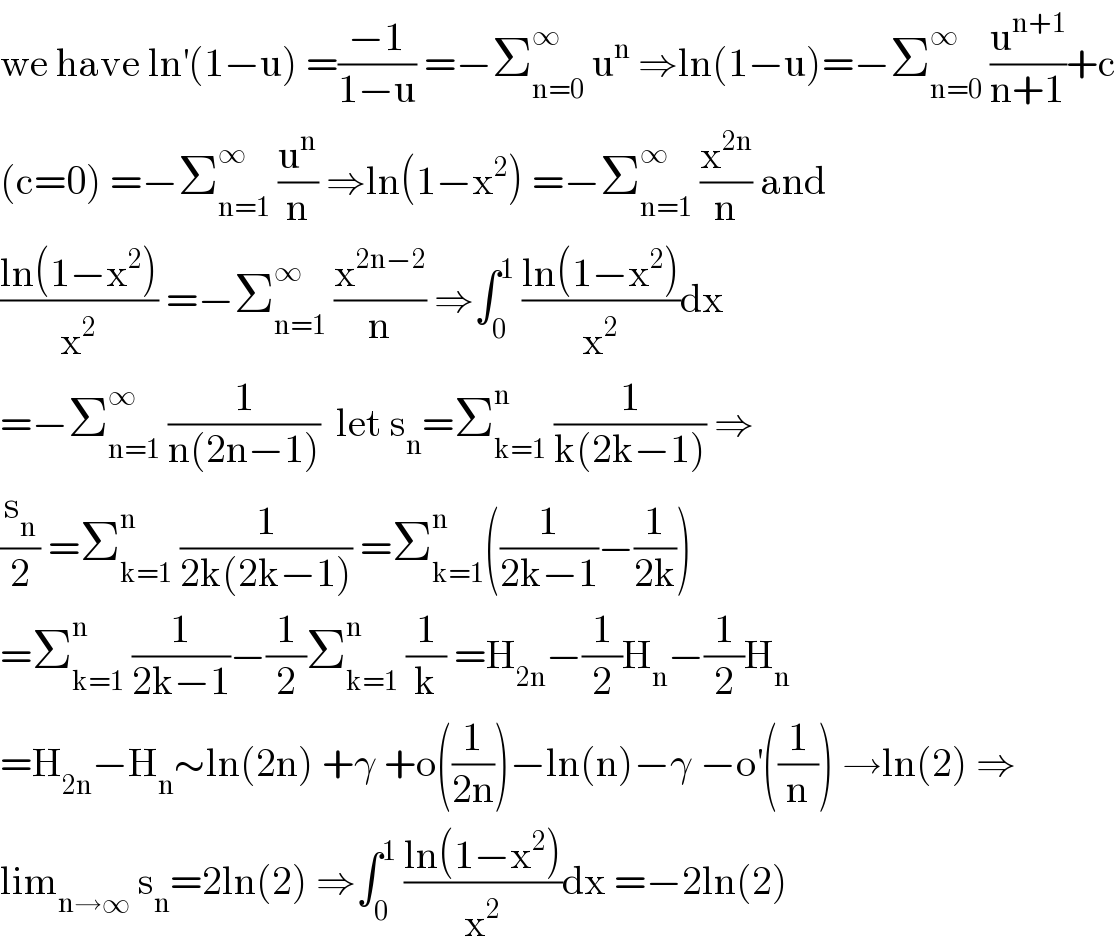 | ||
| ||