Previous in Relation and Functions Next in Relation and Functions
Question Number 94335 by mathmax by abdo last updated on 18/May/20
$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{n}^{\left(−\mathrm{1}\right)^{{n}} } {x}^{{n}} \\ $$
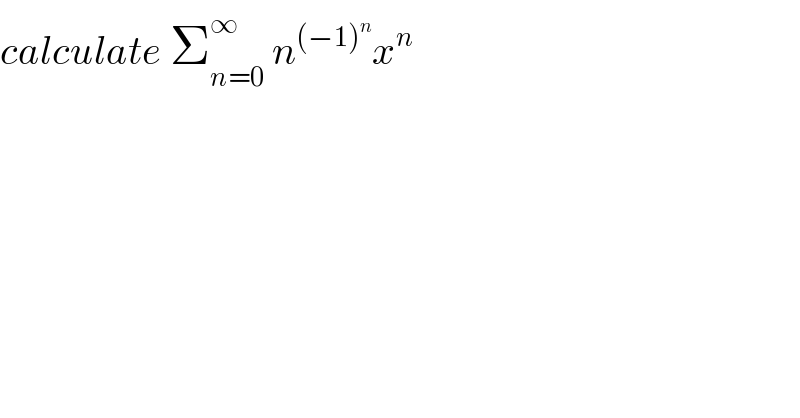
Answered by mathmax by abdo last updated on 19/May/20
![s(x) =Σ_(n=0) ^∞ (2n) x^(2n) +Σ_(n=0) ^∞ (2n+1)^(−1) x^(2n+1) =2 Σ_(n=0) ^∞ nx^(2n) +Σ_(n=0) ^∞ (x^(2n+1) /(2n+1)) =h(x)+k(x) we have Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ Σ_(n=1) ^∞ nx^n =(x/((1−x)^2 )) ⇒Σ_(n=1) ^∞ nx^(2n) =(x^2 /((1−x^2 )^2 ))=h(x) k(x) =Σ_(n=0) ^∞ (x^(2n+1) /(2n+1)) ⇒k^′ (x) =Σ_(n=0) ^∞ x^(2n) =(1/(1−x^2 )) ⇒ k(x) =∫_0 ^x (dt/(1−t^2 )) +k (k=0) =(1/2)∫_0 ^x ((1/(1−t))+(1/(1+t)))dt =(1/2)[ln∣((1+t)/(1−t))∣]_0 ^x =(1/2)ln∣((1+x)/(1−x))∣ ⇒s(x) =((2x^2 )/((1−x^2 )^2 )) +(1/2)ln∣((1+x)/(1−x))∣ with ∣x∣ <1](Q94485.png)
$$\mathrm{s}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{2n}\right)\:\mathrm{x}^{\mathrm{2n}} \:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\mathrm{2n}+\mathrm{1}\right)^{−\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{nx}^{\mathrm{2n}} \:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\:=\mathrm{h}\left(\mathrm{x}\right)+\mathrm{k}\left(\mathrm{x}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{2n}} \:=\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{h}\left(\mathrm{x}\right) \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\:\Rightarrow\mathrm{k}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\mathrm{k}\:\:\:\left(\mathrm{k}=\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{x}} \left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\mid\right]_{\mathrm{0}} ^{\mathrm{x}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}\mid\:\Rightarrow\mathrm{s}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}\mid\: \\ $$$$\mathrm{with}\:\mid\mathrm{x}\mid\:<\mathrm{1} \\ $$
Answered by maths mind last updated on 18/May/20
$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\mathrm{2}{nx}^{\mathrm{2}{n}} −\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\mathrm{2}{n}+\mathrm{1}\right){x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${s}=\underset{{n}\geqslant\mathrm{1}} {\sum}\mathrm{2}{nx}^{\mathrm{2}{n}} −{x}\underset{{n}\geqslant\mathrm{0}} {\sum}\mathrm{2}{nx}^{\mathrm{2}{n}} −{x}\underset{{n}\geqslant\mathrm{0}} {\sum}{x}^{\mathrm{2}{n}} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}{nx}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\Sigma\mathrm{2}{nx}^{\mathrm{2}{n}} =\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow{s}=\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{\mathrm{2}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${s}=\frac{−{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
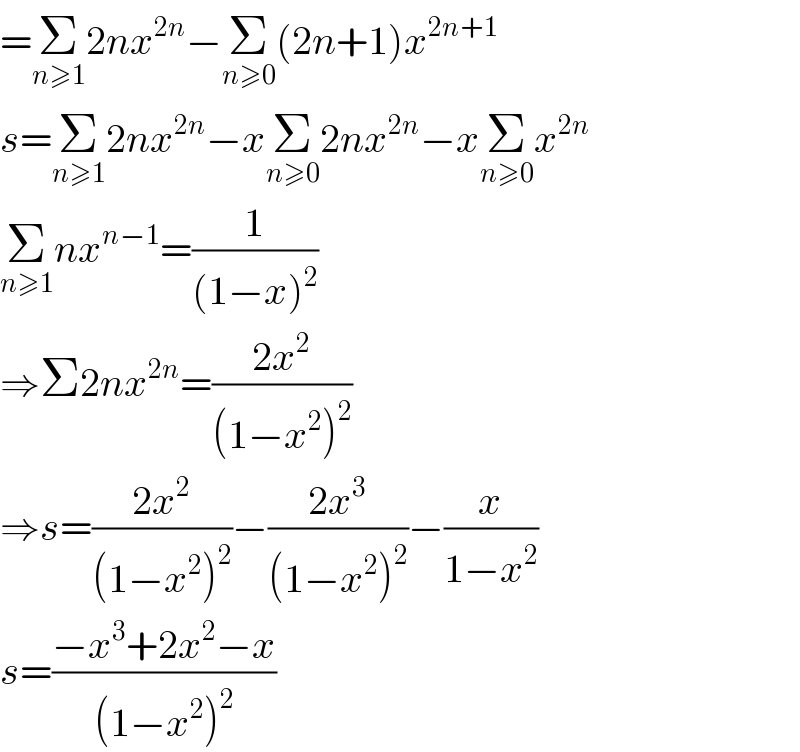
Commented by mathmax by abdo last updated on 19/May/20
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$